2. 厦门理工学院应用数学学院, 福建 厦门 361024
2. School of Applied Mathematics, Xiamen University of Technology, Xiamen 361024, China
1 引言
倒立摆系统是一类典型的不稳定、 非线性对象,其控制方法能够应用在机器人行走控制和飞行器姿态控制等多个领域[1]. 自20世纪70年代初期开始,用状态反馈理论对不同类型的倒立摆进行姿态控制是当时的一类研究热点. 文[2]针对一类双轴非线性倒立摆系统,采用自适应滑模控制实现了倒立摆的精确跟踪控制. 文[3]考虑了轮式倒立摆的动态平衡控制和位置控制,提出了一种基于李亚普诺夫稳定性定理的自适应鲁棒控制方法. 文[4]在二级倒立摆摆角控制中,考虑了摆杆的角度信号受到噪声影响的情况,给出了卡尔曼滤波器增益矩阵的设计方法. 理论设计虽然能够实现倒立摆系统的高性能控制,但在实际应用中,还需考虑复杂环境中存在的干扰和不确定性对系统的影响,才能更好地确保这类控制系统的实际运行.
自抗扰控制是一类不依赖于被控对象精确模型的先进控制方法,目前在工业控制的各个领域应用广泛,被认为是能够代替传统PID控制的一类简单有效的新方法[5]. 自抗扰控制是我国学者韩京清对“反馈系统中线性与非线性关系”的探讨和“控制理论——模型论还是控制论”的思考中逐步发展起来的[6]. 其核心思想在于,构建扩张状态实现等效扰动补偿,使系统具备“串联积分标准型”结构,并通过状态反馈重新构造控制系统的动态特性,使其达到理想的控制性能.
扩张状态观测器(extended state observer, ESO)是自抗扰控制的核心部分. ESO是以“串联积分标准型”为理想对象建立起来的一类观测器. 由于被控对象“串联积分”之外的系统特性与外部扰动扩张成了一个新的状态,利用ESO能够实现扩张状态观测和反馈补偿. 可见,扩张状态能实现等效扰动的建模. 需要指出的是,ESO只有在镇定控制的条件下才能有效工作,否则等效扰动发散会使得观测误差无法收敛. 在具有扩张状态的反馈线性化结构下,状态反馈恰好能够提供必要的镇定控制作用. 大量理论分析和实验表明,基于扰动补偿的控制结构设计和镇定控制相结合,能够实现高性能控制[7-8].
利用自抗扰控制的优良鲁棒性能,许多学者将自抗扰控制方法应用于倒立摆系统上,并取得了良好效果[9-11]. 本文以一类直线倒立摆为对象,通过设计自抗扰摆角控制器,在具有周期扰动、 模型不确定性或间隙迟滞非线性的复杂条件下,开展倒立摆系统的摆角控制实验研究. 通过分析可知,该方法能够将这三类影响因素等效成控制系统的输入端扰动,仿真实验结果验证了倒立摆系统能够在复杂条件下达到良好的摆角控制效果.
2 倒立摆系统摆角模型本文采用固高公司生产的一类直线倒立摆进行摆角控制设计. 倒立摆系统由一级摆杆、 小车、 角度编码器、 导轨和固高GT系列运动控制器等装置构成. 忽略空气阻力和各种摩擦之后,一级直线倒立摆系统抽象成小车和匀质杆组成的系统,如图 1所示. 表 1给出了系统的物理参数.
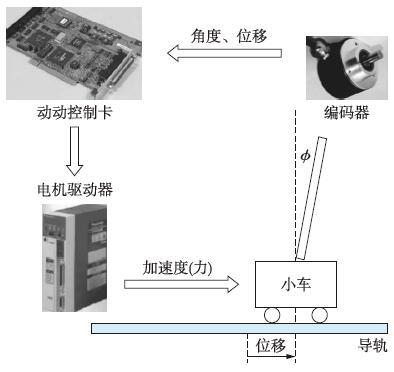
|
| 图 1 倒立摆系统示意图 Figure 1 Diagram of inverted pendulum system |
| 符号 | 数值 | 含义 |
| M | 1.096 kg | 小车质量 |
| m | 0.109 kg | 摆杆质量 |
| l | 0.25 m | 摆杆质心到转轴的距离 |
| b | 0.1 N/m/s | 小车的滑动摩擦系数 |
| I | 0.003 4 kg | 摆杆转动惯量 |
| T | 0.005 s | 采样周期 |
| x | m | 小车相对初始位置的位移 |
| θ | rad | 摆杆与垂直向下方向的夹角 |
| φ | rad | 摆杆与垂直向上方向的夹角 |
对倒立摆系统进行受力分析,建立系统的运动方程[12]:
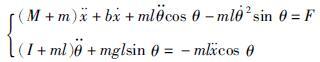
|
(1) |
式(1)中存在关于角度的三角函数,属于一类非线性方程. 考虑到在倒立摆摆角控制中,φ一般较小,有cos θ≈-1,sin θ=-φ. 在φ较小(φ<10°)的条件下,以小车加速度为控制输入u, 摆杆角度φ为输出,建立系统(1)的近似状态方程:
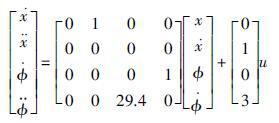
|
(2) |
其传递函数为
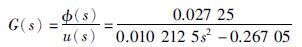
|
(3) |
从系统传递函数可以看出,摆角模型为二阶不稳定系统,存在一个右半平面极点s=5.113. 在实际物理系统中,倒立摆摆杆在竖直向上不受外力的条件下将不能保持平衡. 可见,对非线性进行近似处理后,系统模型仍然能够反应实际系统的物理特性.
2.2 三类影响因素式(2)或式(3)给出了倒立摆系统在理想条件下的摆角模型,而在实际运行条件下,系统可能受到干扰和不确定性影响,使得系统模型与实际对象存在较大误差. 考虑倒立摆系统可能受到的三类影响因素,将其等效为输入端的扰动进行补偿控制.
第一类影响因素是机械系统普遍存在的周期扰动. 电机运转振动或电网谐波等因素都能引起机械系统产生周期性的扰动,使得系统的控制性能降低. 可以将其等效成输入端扰动进行考虑[13],即
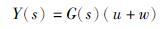
|
(4) |
其中,w为周期性扰动,具有非衰减振荡特征.
第二类影响因素是系统建模过程中必然存在的模型误差或不确定性. 用G*(s)表示实际物理系统,G(s)表示系统模型,利用乘法不确定性描述:
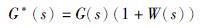
|
(5) |
将W(s)定义为不改变系统相对阶数、 不引入非最小相位零点的不确定因子,其对系统的影响可描述成输入端的前馈扰动,则
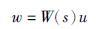
|
(6) |
第三类影响因素为机械传动系统中存在的齿轮间隙. 倒立摆是通过控制小车运动来实现摆杆角度的调节,而小车主要靠导轨两端的电机带动齿轮和皮带来实现传动. 齿轮间存在的间隙迟滞会对倒立摆控制产生一定的影响,特别是传动设备老化或磨损后,间隙迟滞对系统的影响不可忽视. 常见的间隙迟滞描述模型为v(t)=P(u(t)),其中u(t)和v(t)分别为迟滞的输入和输出,P为迟滞算子,可以表示为backlash的形式
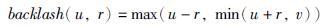
|
(7) |
其中,r为间隙阈值. 其关系可用微分方程来描述[14]:
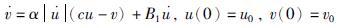
|
(8) |
其中,α,c, B1为常数,且c>B1,α>0. 式(8)的解为
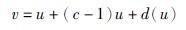
|
(9) |
其中,
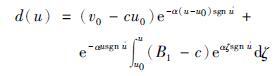
|
(10) |
可见,间隙迟滞也可以表示为一类输入端的前馈扰动:

|
(11) |
因此,倒立摆系统摆角控制的目的在于设计一个反馈控制作用使系统产生合适的小车加速度(即小车受力),驱动倒立摆摆杆运动,保持竖直向上状态,并使系统在复杂条件下良好稳定地工作.
3 自抗扰控制器设计自抗扰控制器继承了经典PID控制不依赖对象模型的优点,并改进了PID控制在快速性和超调量不能兼顾的缺陷,是一类结构简单的新型控制器.
针对倒立摆的二阶摆角模型,考虑二阶系统的自抗扰控制. 假设系统模型为
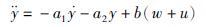
|
(12) |
式中,u为系统的输入,y为输出,w为输入端扰动. w包含了上文提到可能存在的3种复杂影响因素(式(4)、 式(6)或式(11)).
3.1 ESO设计令x1=y, x2=
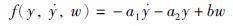
|
(13) |
为系统广义扰动,其包含了系统内部不确定性和输入端扰动,将其扩张为系统的状态变量
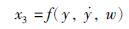
|
(14) |
对系统(2)进行状态变换,可以得到新的状态方程
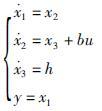
|
(15) |
式中,x1,x2,x3为系统状态变量.
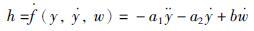
|
(16) |
其中,a1=0,a2=-26.15,b=2.668.
自抗扰控制的核心思想之一就是将系统存在的广义扰动当作系统内部的一个扩张状态来处理. 在状态方程中,由于涉及到该状态的变化率,即扰动的变化率,使得设计过程考虑了扰动的动态特性. 这样,扰动抑制效果将得到极大的提升.
针对等效系统(9),本文采用高志强教授提出的线性扩张状态观测器(linear extended state observer, LESO)[15]:
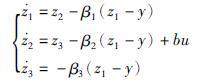
|
(17) |
通过选取合适的观测器增益β1,β2,β3,线性扩张状态观测器能实现对系统(2)中各变量的实时跟踪,即
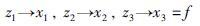
|
(18) |
备注1 需要指出的是,ESO需要在镇定控制的前提下才能有效工作,否则由于系统的不稳定输出引起等效扰动变化率发散,使得观测误差无法收敛. 可以通过分析观测器误差得到以上结论.
令ei=xi-zi,i=1,2,3,结合式(17)和式(18),系统的观测误差方程为
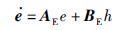
|
(19) |
其中,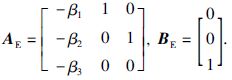
式(19)的解为
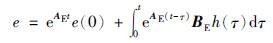
|
(20) |
可见,观测误差的收敛性除了由观测器增益决定外,还要求h有界. 在式(16)中,可以假定输入端扰动变化率有界.
在LESO中,对式(18)进行极点配置,设
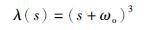
|
(21) |
则β1=3ωo,β2=3ωo2,β3=ωo3. 可以近似地认为ωo为观测器带宽. ωo越大,观测器误差收敛速度越快. 为了后续控制系统参数设计,在此给出p阶无超调系统(ω/s+ω)p的带宽ωb的表达式:
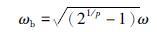
|
(22) |
在一定的镇定控制作用u0的输入下,构造控制率:

|
(23) |
则系统被近似线性化,变成串联积分的标准形式:
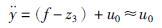
|
(24) |
在具有扩张状态的反馈线性化结构下,利用观测状态z1和z2构造状态反馈,实现必要的镇定控制. 取
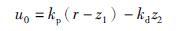
|
(25) |
式中,r为给定信号,kp和kd为反馈控制器增益. 状态反馈式(25)构成了PD控制器. 此时,闭环系统可近似表示为
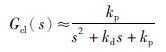
|
(26) |
将式(26)设计成一类典型的无超调系统,

|
(27) |
则有,
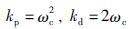
|
(28) |
其中,可以近似认为ωc为闭环系统带宽.
在上述分析中,控制系统的设计归结为2个带宽参数的选取,ωc和ωo. 并且可以在直观上认为,观测器误差的收敛速度越快,系统能够越快实现反馈线性化,这样所得观测状态越准确. 因此,可以近似地选取ωo=3~10ωc.
备注2 通过以上分析,对控制系统进行了反馈线性化和状态反馈控制. 但两者在原理上需要互为前提条件. 例如: ESO设计需要在镇定控制的条件下才能有效工作,而反馈控制是在串联积分标准型的观测状态下进行的. 因此,控制系统的2个带宽参数设计需要在满足闭环系统稳定性条件下才能确保系统的控制性能.
利用劳斯稳定判据对系统的稳定性进行分析和验证. 在频域分析中,自抗扰控制能够等效成一类典型的输出反馈控制结构[16],如图 2所示.
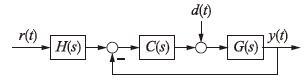
|
| 图 2 自抗扰控制的等效输出反馈 Figure 2 The equivalent output-feedback of ADRC |
在图 2中,反馈控制器和前馈控制器分别为
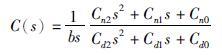
|
(29) |
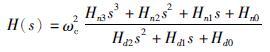
|
(30) |
其中各系数在表 2中给出. 显然,前馈控制器是一类稳定的传递函数,且对系统闭环稳定性不产生影响. 因此,只需关注闭环反馈控制部分的稳定性即可.
| Cn2=3ωc2ωo+6ωcωo2+ωo3 | Hn3=1 |
| Cn1=3ωc2ωo2+2ωcωo3 | Hn2=3ωo |
| Cn0=ωc2ωo3 | Hn1=3ωo2 |
| Cd2=1 | Hn0=ωo3 |
| Cd1=2ωc+3ωo | Hd2=Cn2 |
| Cd0=ωc2+3ωo2+6ωcωo | Hd1=Cn1 |
| Hd0=Cn0 |
首先,分析倒立摆控制系统的带宽设计范围. 由于系统带宽会受到采样频率等物理条件限制,故仅能在一定带宽条件下考虑控制系统参数设计. 在此,需要对实际系统的可达带宽进行估计.
根据采样周期,可知采用频率为
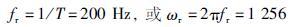
|
(31) |
对实际控制系统而言,为了保证控制系统的动态性能及抗干扰能力,采样周期的选择往往要远大于香农采样定理要求的ωr≥2ωb,一般闭环系统的带宽要求满足ωr≥20ωb,考虑到控制字长和机械结构谐振频率等因素影响,进行保守选取,ωb<20. 根据式(22)可知,ωc<31.
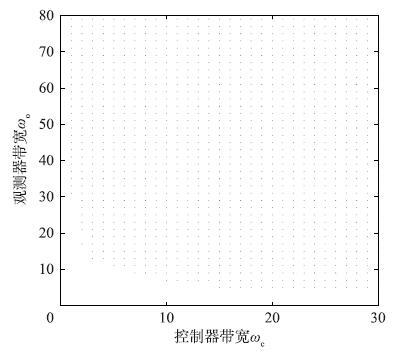
4.2 稳定性分析根据倒立摆系统摆角模型,建立图 2所示的自抗扰控制的等效输出反馈控制结构,在给定的带宽范围内,利用劳斯稳定判据判断闭环特征方程1+G(s)C(s)=0的特征根分布情况,得到满足稳定性条件的参数稳定区域,见图 3中的阴影区域.
|
| 图 3 ωc和ωo的稳定区域 Figure 3 Stable regions of ωc and ωo |
在Matlab/Simulink环境下选取ωo=4ωc进行仿真控制研究. 在图 3所示的镇定区域,选取ωc=4,5,6,7,8,9进行对比分析,对应的增益和相位裕度在表 3中给出. 可以得到,在选定的不同闭环系统带宽条件下,控制系统都能达到较好的稳定裕度,特别是随着ωc的增大,所达到的稳定裕度越大,鲁棒性越好.
| 参数 | GM/dB | PM(°)(rad/dec) |
| ωc=4,ωo=16 | -1.26(2.72) | 31.8(5.45) |
| ωc=5,ωo=20 | -4.12(3.41) | 37.9(9.34) |
| ωc=6,ωo=24 | -6.19(4.09) | 38.6(12.3) |
| ωc=7,ωo=28 | -7.72(4.77) | 38.8(14.9) |
| ωc=8,ωo=32 | -8.80(5.45) | 38.9(17.9) |
| ωc=9,ωo=36 | -9.78(6.13) | 39.0(20.1) |
在实验平台上搭建如图 4所示的自抗扰控制结构,其中实验系统通过图中模块“GT400-SV initialization”实现对运动采集卡进行初始化; 模块“real control”是倒立摆的实时控制模块,实现对倒立摆小车的加速度(力)输入、 小车位置与摆杆角度的实时数据采集.
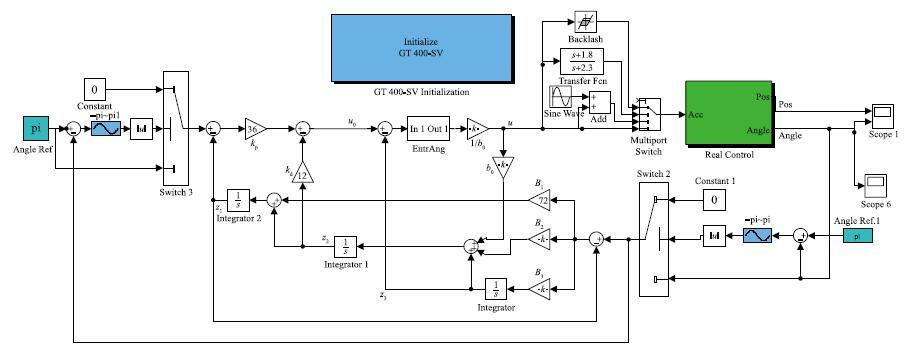
|
| 图 4 摆角控制实验结构图 Figure 4 Experimental structure diagram of pendulum angle control |
在固高实验系统中,当摆杆竖直向下时摆角测量值为0. 因此,设定摆杆垂直向上的角度为π. 当摆杆角度达到π附近时,系统进入自动控制状态.
首先,在无扰条件下对倒立摆系统进行仿真和实验. 此时,图 4中的控制作用不受外部扰动、 模型不确定性和迟滞非线性影响,直接作用于倒立摆小车. 倒立摆系统在ESO的扰动补偿与反馈控制作用下,闭环系统近似一类无超调系统(27),且响应速度与ωc成正比.
图 5和图 6分别给出了倒立摆系统在仿真和实验中的系统响应. 在图 5的仿真控制中,ωc=20时的响应速度和超调量均优于ωc=6时的响应. 而在图 6的实际控制中,ωc=6时的摆角控制振幅约为0.002 4 rad(0.137 5°),明显小于ωc=20时的摆角振幅0.048 rad(2.75°). 实验表明: 由于系统受到带宽等物理因素限制,实际系统无法达到理论设计中的理想效果.
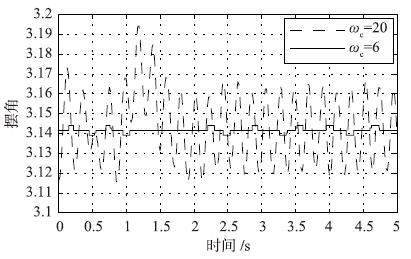
|
| 图 5 阶跃响应对比(ωc=6,20,ωo=4ωc) Figure 5 Step responses comparison (ωc=6,20,ωo=4ωc) |
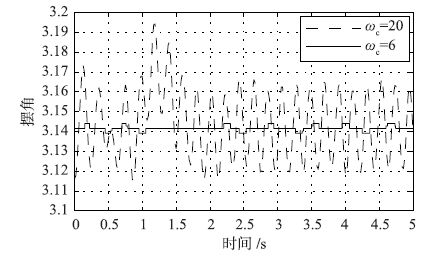
|
| 图 6 实时摆角控制(ωc=6,20,ωo=4ωc) Figure 6 Pendulum angle control in the real time(ωc=6,20,ωo=4ωc) |
进一步,针对倒立摆系统中存在的三类影响因素,在系统输入端加入外部周期扰动、 模型不确定性和齿轮间隙迟滞非线性:
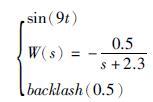
|
(32) |
在给定控制系统参数ωc=8,ωo=64下进行仿真与实验. 将三类影响因素等效成系统的输入端扰动,在阶跃输入条件下,扰动输出效果如图 7所示.
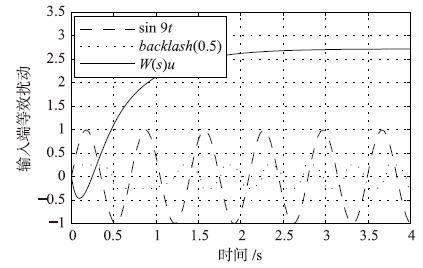
|
| 图 7 三类输入端等效扰动(ωc=8,ωo=64) Figure 7 Three inputs equivalent disturbance (ωc=8,ωo=64) |
根据式(19)给出的ESO观测误差可知: 当等效扰动的导数h趋于0时,即
图 8和图 9分别给出了系统仿真和实验的控制效果. 由图 8的仿真控制可知,在自抗扰控制作用下,输入端周期性扰动的幅值在输出端被极大地削弱,仅为原始信号的1%. 在图 9(b)给出的实时摆角控制也具有类似的效果,当系统进入稳态后(约2 s后),图 9(b)的输出与图 9(a)中标称系统的摆角输出仅有微小的差别.
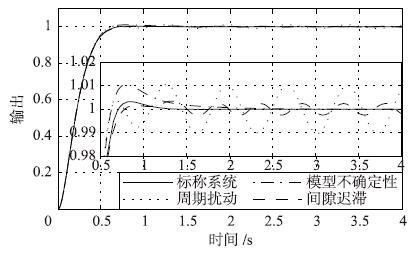
|
| 图 8 复杂条件下的摆角控制仿真(ωc=8,ωo=64) Figure 8 Simulation of the pendulum angle control under complex conditions (ωc=8,ωo=64) |
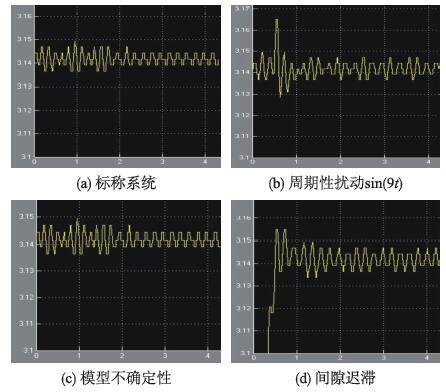
|
| 图 9 复杂条件下的实时摆角控制(ωc=8,ωo=64) Figure 9 Real time pendulum angle control under complex conditions (ωc=8,ωo=64) |
由于引入的模型不确定性不改变系统的相对阶数,也不引入任何非最小相位零点,且等效扰动的导数趋于0. 仿真效果图 8表明,当系统进入稳态后,等效扰动对系统的影响完全被消除; 而实时控制效果图 9(c)的稳态部分也与标称系统效果图 9(a)的稳态部分几乎完全一致. 因此,理论分析和实验结果都表明,这一类模型不确定性能够被完全补偿.
间隙迟滞客观存在于实际控制系统,会使控制系统产生周期性波动. 由于其等效扰动的导数不趋于0,在自抗扰控制的作用下,这种影响只能削弱而不能被完全消除. 从仿真效果图 8可看出,间隙迟滞对系统的影响与周期性扰动是类似的,其等效扰动的幅值在输出端被极大地削弱. 实时控制效果图 9(d)在稳态后,相对于图 9(a)的稳态部分,也表现出微弱的波动特性.
以上实验结果表明,倒立摆系统在自抗扰控制作用下,能够较好地克服复杂环境对系统的影响,保持良好的摆角控制效果.
需要指出的是,在分析过程中,我们将三类影响因素转化为系统输入端的等效扰动,并给出了等效扰动表达式. 但在自抗扰摆角控制设计中,无需用到扰动信息. 因此,这三类等效扰动都属于未知扰动,能够较好地描述复杂环境对系统的影响. 在某些极端环境中,系统可能受到持续的强烈外部干扰,例如强风、 大推力等. 通常这类干扰可以用速度信号、 加速度信号或多项式信号来描述,不论哪种形式,都可以认为干扰信号的某高阶导数有界或趋于0,因此构造具有多个扩张状态的ESO[17-20],使控制系统抑制或消除这类强扰动对系统的影响.
5 结语本文介绍了复杂条件下自抗扰控制方法在倒立摆系统摆角控制上的应用. 首先,将机械系统普遍存在的周期扰动、 模型不确定性和间隙迟滞非线性等三类影响因素等效成控制系统的输入端扰动. 然后,基于自抗扰控制思想,利用扩张状态对输入端扰动和内部不确定性进行建模和估计,通过设计扩张状态观测器和状态反馈控制器,实现了复杂条件下倒立摆系统的高精度摆角控制. 最后,在固高公司生产的一类直线倒立摆上进行了仿真和实验,实验结果表明在一定的带宽条件下,自抗扰控制方法能够很好地克服外部周期性扰动、 模型不确定性和间隙迟滞非线性等因素对系统的影响,并保证良好的控制效果.
| [1] | Li Z, Yang C. Neural-adaptive output feedback control of a class of transportation vehicles based on wheeled inverted pendulum models[J]. IEEE Transactions on Control Systems Technology , 2012, 20 (6) : 1583–1591. DOI:10.1109/TCST.2011.2168224 |
| [2] | Wai R J, Chang L J. Adaptive stabilizing and tracking control for a nonlinear inverted-pendulum system via sliding-mode technique[J]. IEEE Transactions on Industrial Electronics , 2006, 53 (2) : 674–692. DOI:10.1109/TIE.2006.870680 |
| [3] | Li Z, Luo J. Adaptive robust dynamic balance and motion controls of mobile wheeled inverted pendulums[J]. IEEE Transactions on Control Systems Technology , 2009, 17 (1) : 233–241. DOI:10.1109/TCST.2008.924579 |
| [4] | 祁虔, 李祖枢, 谭智, 等. 基于卡尔曼滤波的倒立摆控制系统噪声抑制[J]. 控制与决策 , 2010, 25 (8) : 1144–1148. Qi Q, Li Z S, Tan Z, et al. Noise suppression of inverted pendulum system based on Kalman filter[J]. Control and Decision , 2010, 25 (8) : 1144–1148. |
| [5] | Han J Q. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics , 2009, 56 (3) : 900–906. DOI:10.1109/TIE.2008.2011621 |
| [6] | 韩京清. 控制理论——模型论还是控制论[J]. 系统科学与数学 , 1989, 9 (4) : 328–335. Han J Q. Control theory: Model approach or control approach[J]. Journal of Systems Science and Mathematical Sciences , 1989, 9 (4) : 328–335. |
| [7] | Dong L L, Zhang Y, Gao Z Q. A robust decentralized load frequency controller for interconnected power systems[J]. ISA Transactions , 2012, 51 (3) : 410–419. DOI:10.1016/j.isatra.2012.02.004 |
| [8] | Zhao S, Gao Z. Modified active disturbance rejection control for time-delay systems[J]. ISA Transactions , 2014, 53 (4) : 882–888. DOI:10.1016/j.isatra.2013.09.013 |
| [9] | 武利强, 韩京清. 直线型倒立摆的自抗扰控制设计方案[J]. 控制理论与应用 , 2004, 21 (5) : 665–670. Wu L Q, Han J Q. Active disturbance rejection controller scheme for the linear inverted pendulum[J]. Control Theory and Applications , 2004, 21 (5) : 665–670. |
| [10] | 高强, 陈莎莎, 李毅. 线性自抗扰控制在倒立摆系统的实现[J]. 电气传动 , 2014, 44 (10) : 49–53. Gao Q, Chen S S, Li Y. Application of LADRC on inverted pendulum system[J]. Electric Drive , 2014, 44 (10) : 49–53. |
| [11] | 马燕, 夏超英. 单级旋转倒立摆的自抗扰控制[J]. 电气传动 , 2007, 37 (6) : 39–41. Ma Y, Xia C Y. Active disturbance rejection control scheme for the single-rotational inverted pendulum[J]. Electric Drive , 2007, 37 (6) : 39–41. |
| [12] | 固高公司. 固高倒立摆与自动控制原理实验V2.0[Z]. 深圳: 固高科技(深圳)有限公司, 2005. GOOGOLTECH. Inverted pendulum of GOOGOLTECH and the experiment of automatic control V2.0[Z]. Shenzhen: Googol Technology Limited, 2005. http://www.doc88.com/p-9923957618007.html |
| [13] | She J H, Fang M, Ohyama Y, et al. Improving disturbance-rejection performance based on an equivalent-input-disturbance approach[J]. IEEE Transactions on Industrial Electronics , 2008, 55 (1) : 380–389. DOI:10.1109/TIE.2007.905976 |
| [14] | Su C Y, Stepanenko Y, Svoboda J, et al. Robust adaptive control of a class of nonlinear systems with unknown backlash-like hysteresis[J]. IEEE Transactions on Automatic Control , 2000, 45 (12) : 2427–2432. DOI:10.1109/9.895588 |
| [15] | Gao Z Q. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the 2003 American Control Conference. Piscataway, NJ, USA: IEEE, 2003: 4989-4996. |
| [16] | Tian G, Gao Z. Frequency response analysis of active disturbance rejection based control system[C]//IEEE International Conference on Control Applications. Piscataway, NJ, USA: IEEE, 2007: 1595-1599. |
| [17] | Zurita-Bustamante E W, Linares-Flores J, Guzman-Ramirez E, et al. A comparison between the GPI and PID controllers for the stabilization of a DC-DC “buck” converter: A field programmable gate array implementation[J]. IEEE Transactions on Industrial Electronics , 2011, 58 (11) : 5251–5262. DOI:10.1109/TIE.2011.2123857 |
| [18] | Gutiérrez-Giles A, Arteaga-Pérez M A. GPI based velocity/force observer design for robot manipulators[J]. ISA Transactions , 2014, 53 (4) : 929–938. DOI:10.1016/j.isatra.2014.03.002 |
| [19] | Sun J K, Yang J, Li S H. Disturbance and plant uncertainties attenuation for a class of nonlinear systems using GPI technique[C]//Proceedings of the 34th Chinese Control Conference. Piscataway, NJ, USA: IEEE, 2015: 967-972. |
| [20] | Sira-Ramirez H, Ramirez-Neria M, Rodriguez-Angeles A. On the linear control of nonlinear mechanical systems[C]//49th IEEE Conference on Decision and Control. Piscataway, NJ, USA: IEEE, 2010: 1999-2004. |



