2. 大庆油田有限责任公司天然气分公司, 黑龙江 大庆 163318
2. Natural Gas Branch Company of Daqing Oilfield Co. Ltd, Daqing 163318, China
1 引言
在通信或控制应用领域中,H∞滤波相对于古典卡尔曼滤波,能够在无需噪声统计信息的情形下,提供最坏状况的估计误差界限[1].大多数H∞滤波器设计方法假定参数可以精确执行[2],然而在工程应用中,由于数模转换的不精确,数值取整误差、控制器增益重调、执行器老化等原因,在滤波器中是存在参数波动的.更重要的是,一些设计方法的滤波器对系数误差是敏感的[3],相对小的波动可能会导致系统性能下降,甚至是不稳定.因此,研究设计能够抵抗一定程度增益变化的非脆弱滤波器十分重要[4],如文[5]设计了具有参数摄动的离散系统的鲁棒非脆弱H∞滤波器.此外,在现代网络控制系统(networked control systems,NCSs)的传输和执行过程中,网络引起的截断、饱和、突发负载变化等,会导致随机发生增益变化(randomly occurring gain variations,ROGVs)现象,其中增益变化按一定强度、类型随机发生.文[6]设计了考虑ROGVs现象的离散时间系统非脆弱H∞控制器,在控制输入中加入了高斯分布的随机变量和乘性增益变化,得到的闭环系统具有良好的收敛性能且不受控制器增益波动的影响.然而,伴有ROGVs的离散系统非脆弱H∞滤波问题尚未得到足够研究,本文在随机非脆弱控制问题基础上,进一步研究其滤波算法.
在控制工程和信号处理领域,连接网络元件的通信电缆通常是有限带宽的,这会导致通信时滞[7]、量化误差[8]、数据丢失[9]、非线性[10]等现象.在多种时滞中,分布时滞由于其工程意义,得到越来越多的关注[11],在文[12]中,考虑了时变分布时滞系统的H∞滤波器设计.在诸如运动材料热加工、图像处理、联想记忆等实际系统中,也广泛存在着无穷分布时滞.从客观实际角度上讲,无穷分布时滞[13]能够进一步描述事物本质,含无穷分布时滞的系统由n个含时滞的线性系统构成,因此,离散时滞系统为无穷分布时滞系统的一种特殊情形[14].近来已有关于连续时间系统的研究结果,其中无穷分布时滞由有限或无穷积分描述.然而,当前的数字控制系统本质上是离散的[15],关于具有无穷分布时滞的离散时间系统滤波器设计,研究成果还很少,本文参考[6, 14]中无穷分布时滞的研究模型,推导离散时滞系统的非脆弱H∞滤波问题.
在网络化系统控制和滤波问题中,一种对于随机丢失测量现象的建模方法是采用二进制随机变量序列[16-18].在文[16]中,研究了带丢失测量的方差约束滤波问题,得到的滤波器可以确保每个状态估计误差的稳态方差低于一个给定界限.文[17]考虑了带有丢失测量现象的时滞系统鲁棒H∞滤波问题,并就确定的线性矩阵不等式,给出解决办法.文[18]研究了一类带丢失测量的非线性随机系统H∞滤波问题.
本文研究同时考虑随机丢失测量、无穷分布时滞、ROGVs的离散系统非脆弱H∞滤波问题.由于系统模型中包含诸多因素,在经过加强的随机分析过程后,设计出符合要求的滤波器.
注 MT为矩阵M的转置;Rn表示n维欧几里得空间,Rn×m为n×m阶实矩阵集;I和0分别表示单位矩阵和零矩阵;l2([0,∞);Rn)为区间[0,∞)上平方可积的n维向量函数空间;P>0表示P为实对称正定矩阵;E{x}表示随机变量x的期望;||x||表示向量x的欧几里得范数;diag{A1,A2,…,An}表示对角块为矩阵A1,A2,…,An的块对角矩阵;在对称块矩阵中,符号*表示省略的对称项.
2 问题描述考虑如下离散时间系统:
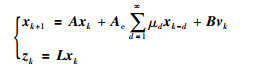
|
(1) |
其中,xk∈Rnx为系统状态向量,zk∈Rnz为控制输出向量,vk∈l2([0,∞);Rq)为外部干扰信号,系统矩阵A、Ae、B和L为已知的适当维数实矩阵,μd≥0(d=1,2,…,∞)为满足如下收敛条件的常数:
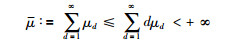
|
(2) |
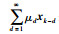
考虑到网络环境中存在的ROGVs现象,设计如下形式的离散时间滤波器:

|
(3) |
其中,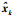
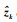

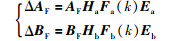
|
(4) |
其中,Ha、Hb、Ea、Eb为已知的适当维数矩阵,Fa(k)、Fb(k)为满足FaT(k)Fa(k)≤I,FbT(k)Fb(k)≤I的未知矩阵.
令
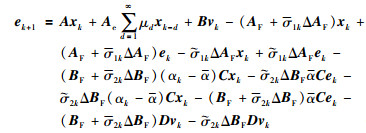
|
(5) |
令η :=[xkT ekT]T,zek=zk-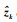
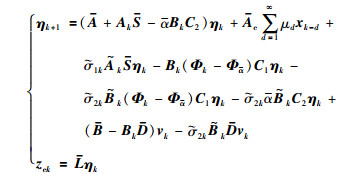
|
(6) |
其中,
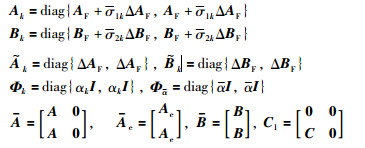
|
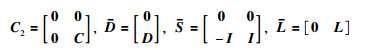
|
本文研究具有随机丢失测量、ROGVs的离散时滞系统(1)的非脆弱H∞滤波,其目标是设计由式(3)、式(4)描述的滤波器,满足以下条件:
a) 当vk=0时,滤波器增广系统(6)渐近稳定;
b) 在零初始条件下,对于给定干扰衰减水平γ>0和非零vk∈l2([0,∞);Rq),估计误差zek满足:
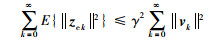
|
(7) |
首先,引入下列引理:
引理1[20] 已知W∈Rnx×nx为正半定矩阵,xi∈Rnx,常数ai>0(i=1,2,…).如果序列{ai}i≥1收敛,得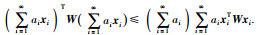
引理2[21] 给定矩阵E=ET,M和N为适当维数的实矩阵,且矩阵F满足FTF≤I,则E+MFN+NTFTMT < 0成立的充分条件是存在正数μ>0,使得E+μMMT+μ-1NTN < 0或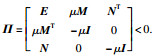
滤波器设计是基于系统稳定的,下面进行当vk=0时系统的稳定性分析,给出如下定理:
定理1 考虑一类具有ROGVs、无穷分布时滞、随机丢失测量的离散系统(1),给定H∞性能指标γ>0,且已知滤波器参数AF、BF,则依据滤波器(3)的增广动态系统(6)渐近稳定,并满足H∞性能约束(7)的充分条件是存在对称正定矩阵P和Q,使得下面的双线性矩阵不等式成立:
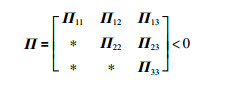
|
(8) |
其中,

|
式中,P=diag{P,P},IB=[I 0],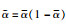
证明 取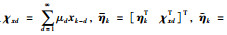
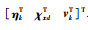

|
(9) |
其中,
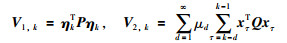
|
(10) |
沿系统(6)的轨线计算V1,k的微分,并取数学期望,得:
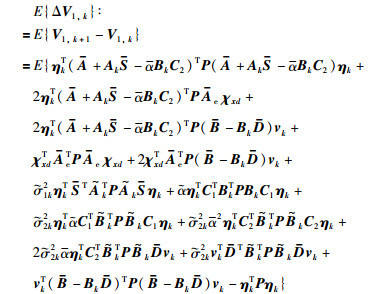
|
(11) |
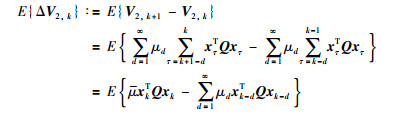
|
(12) |
由引理1可知:
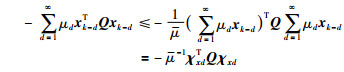
|
(13) |
其中,μ定义如式(2).将式(13)代入式(12)得
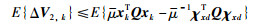
|
(14) |
由于xk=IBηk,得
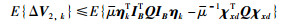
|
(15) |
进而,当vk=0时,结合式(11)、式(15),有:
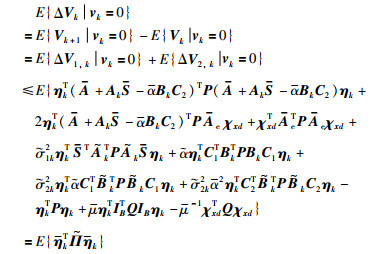
|
(16) |
其中,
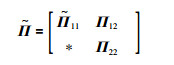
|
(17) |
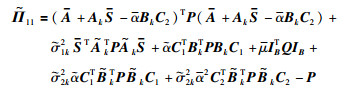
|
根据Schur补引理和式(8)可知,
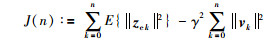
|
(18) |
由式(11),式(15)和式(16),得:
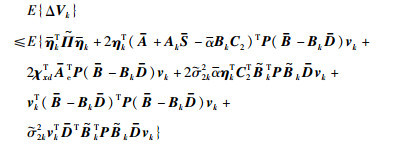
|
(19) |
在零初始条件下,由式(18)得
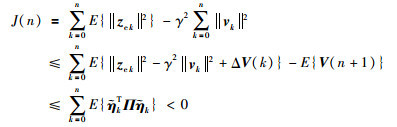
|
(20) |
令n→∞,由上述不等式得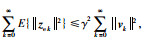
基于定理1,下面讨论非脆弱H∞滤波器设计问题.
定理2 针对具有非脆弱滤波器、无穷分布时滞、随机丢失测量的离散时间系统(1),给定H∞性能指标γ>0,那么滤波器增广系统(6)渐近稳定且满足性能约束(7)的充分条件是存在对称正定矩阵P、Q,矩阵Z11、AF、BF,正常数ε,使得下面线性矩阵不等式成立:
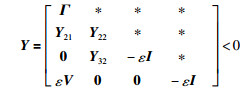
|
(21) |
其中,

|
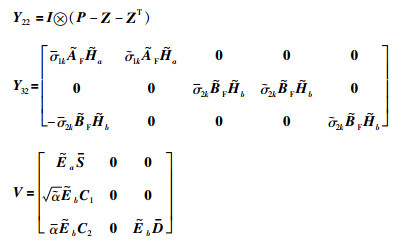
|
式中,Z=diag{Z11,Z11},
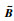
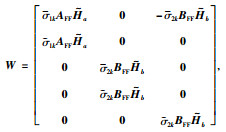
证明 由式(8)得

|
(22) |
其中,
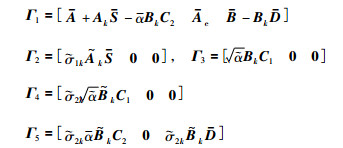
|
利用Shur补引理,式(22)可以转化成
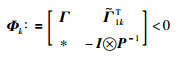
|
(23) |
其中,
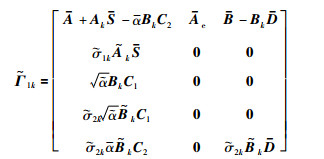
|
进一步地,Φk可分解成:
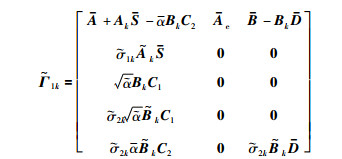
|
(24) |
其中,
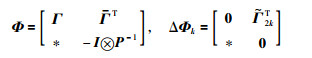
|

|
注意到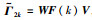
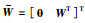
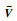
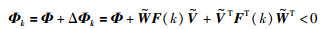
|
(25) |
根据引理2,得
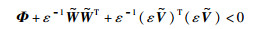
|
(26) |
结合式(24)和式(26),使用Schur补引理,得到不等式(23)是可行的,如果

|
(27) |
成立.
此外,由式(21)得,Z是可逆的.因此,在不等式(27)左右分别乘diag{I,I⊗Z,I,I}与diag{I,I⊗ZT,I,I},并令
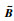
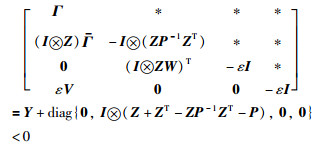
|
(28) |
由于Z+ZT-ZP-1ZT-P-Z=-(P-Z)P-1(P-Z)T≤0,得出如下结论:若Y < 0,不等式(28)成立.因此,根据定理1可知,滤波器增广系统(6)是渐近稳定的,同时满足性能约束(7),证毕.
在定理2中,所得结果包含系统的全部参数,如物理参数,滤波器增益变化及其发生概率,随机丢失测量发生概率等.
4 仿真考虑形式为式(1)的系统,参数如下:
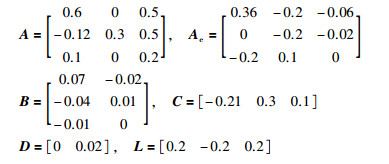
|
令常数序列{μd}d∈[0,∞)为μd=2-3-d,则μ=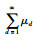
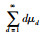

利用Matlab YALMIP 3.0软件[6],得到非脆弱H∞滤波问题的解集如下:

|
滤波器的增益为

|
为进一步说明所设计的非脆弱H∞滤波器的有效性,令干扰为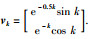
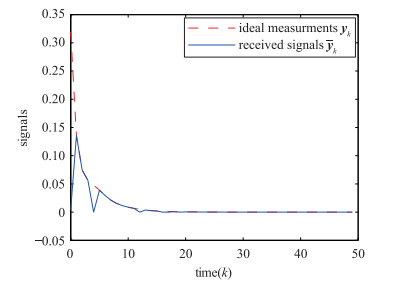
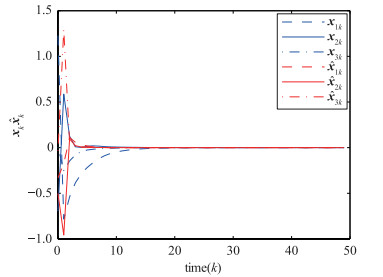
仿真结果如图 1~图 3所示. 图 1中虚线为传感器的理想测量输出;实线为滤波器实际接收到的信号,其中的波动直观地反映了随机丢失测量对测量信号的影响. 图 2描述系统和滤波器的状态,蓝色虚线、实线、点划线表示系统状态x1k、x2k、x3k,红色虚线和实线表示滤波器状态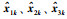
|
| 图 1 理想测量输出与发生丢包的输出 Figure 1 The ideal measurement output and the output with packet dropout |
|
| 图 2 系统和滤波器状态 Figure 2 States of the system and the filter |
|
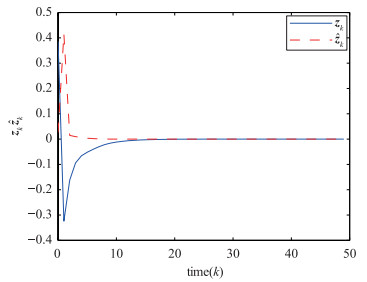
| 图 3 输出zk和它的估计 Figure 3 Output zk and its estimate |
图 3描述了输出zk和它的估计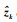
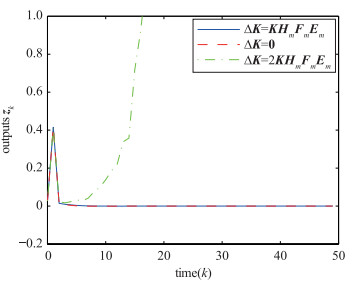
|
| 图 4 不同滤波器增益变化下的输出zk Figure 4 Output zk with different gain variations of the filter |
本文研究了一类具有无穷分布时滞、随机丢失测量及ROGVs的离散系统非脆弱H∞滤波问题.文中通过增广原系统状态和滤波器估计误差,基于李亚普诺夫稳定性理论及加强的随机分析技术,研究了滤波器增广系统稳定性.然后,基于稳定性结果,得到了期望滤波器存在的充分条件.接着,通过确定LMI的可行解,得到滤波器增益.最后,用数值仿真说明了方法的有效性,论文以后的工作为将该结果推广到模糊系统中.
| [1] | Gao H J, Chen T. H∞ estimation for uncertain systems with limited communication capacity[J]. IEEE Transactions on Automatic Control , 2007, 52 (11) : 2070–2084. DOI:10.1109/TAC.2007.908316 |
| [2] | Keel L, Bhattacharya S. Robust, fragile or optimal?[J]. IEEE Transactions on Automatic Control , 1997, 42 (8) : 1098–1105. DOI:10.1109/9.618239 |
| [3] | Yang G H, Wang J L. Robust nonfragile Kalman filtering for uncertain linear systems with estimation gain uncertainty[J]. IEEE Transactions on Automatic Control , 2001, 46 : 343–348. DOI:10.1109/9.905707 |
| [4] | Haddad W M, Corrado J R. Robust resillient dynamic controllers for systems with parametric uncertainty and controller gain variations[C]//Proceedings of American Control Conference. Piscataway, NJ, USA:IEEE, 1998:2837-2841. |
| [5] | 冉华军, 蔡逢煌, 王武, 等. 具有参数摄动离散系统的鲁棒非脆弱H∞滤波[J]. 福州大学学报:自然科学版 , 2008, 36 (3) : 363–368. Ran J H, Cai F H, Wang W, et al. Robust and non-fragile H∞ filtering for discrete-time system with uncertain parameters[J]. Journal of Fuzhou University:Natural Science , 2008, 36 (3) : 363–368. |
| [6] | Shu H S, Li Z N, Wang Z D, et al. Non-fragile H∞ control with randomly occurring gain variations, distributed delays and channel fadings[J]. IET Control Theory and Applications , 2014, 9 (2) : 222–231. |
| [7] | Wang L, Wei G, Shu H. State estimation for complex networks with randomly occurring coupling delays[J]. Neurocomputing , 2013, 122 : 513–520. DOI:10.1016/j.neucom.2013.05.010 |
| [8] | Dong H L, Wang Z D, Gao H J. Distributed filtering for a class of time-varying systems over sensor networks with quantization errors and successive packet dropouts[J]. IEEE Transactions on Signal Processing , 2012, 60 : 3164–3173. DOI:10.1109/TSP.2012.2190599 |
| [9] | Sun S, Xie L, Xiao W, et al. Optimal linear estimation for systems with multiple packet dropouts[J]. Automatica , 2008, 44 (5) : 1333–1342. DOI:10.1016/j.automatica.2007.09.023 |
| [10] | Wang L, Wei G, Li W. Probability-dependent H∞ synchronization control for dynamical networks with randomly varying nonlinearities[J]. Neurocomputing , 2014, 133 : 369–376. DOI:10.1016/j.neucom.2013.12.045 |
| [11] | Gao H J, Lam J, Wang C. Robust energy-to-peak filter design for stochastic time-delay systems[J]. Systems Control & Letters , 2006, 55 (2) : 101–111. |
| [12] | Yu X G. An LMI approach to robust H∞ filtering for uncertain systems with time-varying distributed delays[J]. Journal of the Franklin Institute , 2008, 345 (8) : 877–890. DOI:10.1016/j.jfranklin.2008.05.003 |
| [13] | Wei G L, Han F, Wang L C, et al. Reliable H∞ filtering for discrete piecewise linear systems with infinite distributed delays[J]. International Journal of General Systems , 2014, 43 (3/4) : 346–358. |
| [14] | 赵宁宁.带有无穷分布时滞的离散系统的H∞滤波器设计[D].曲阜:曲阜师范大学, 2011:2-3. Zhao N N. Design of H∞ filter for discrete systems with infinite distributed time delays[D]. Qufu:Qufu Normal University, 2011:2-3. http://cdmd.cnki.com.cn/article/cdmd-10446-1011116747.htm |
| [15] | Wang Z D, Liu Y, Wei G, et al. A note on control of a class of discrete-time stochastic systems with distributed delays and non-linear disturbances[J]. Automatica , 2010, 46 (3) : 543–548. DOI:10.1016/j.automatica.2009.11.020 |
| [16] | Wang Z D, Daniel W C H, Liu X. Variance-constrained filtering for uncertain stochastic systems with missing measurements[J]. IEEE Transactions on Automatic Control , 2003, 48 (7) : 1254–1258. DOI:10.1109/TAC.2003.814272 |
| [17] | Wang Z D, Yang F, Daniel W C H, et al. Robust H∞ filtering for stochastic time-delay systems with missing measurements[J]. IEEE Transactions on Signal Processing , 2006, 54 (7) : 2579–2587. DOI:10.1109/TSP.2006.874370 |
| [18] | Shen B, Wang Z D, Shu H, et al. On nonlinear H∞ filtering for discrete-time stochastic systems with missing measurements[J]. IEEE Transactions on Automatic Control , 2008, 53 (9) : 2170–2180. DOI:10.1109/TAC.2008.930199 |
| [19] | Lien C H, Cheng W C, Tsai C H, et al. Non-fragile observer-based controls of linear system via LMI approach[J]. Chaos, Solitons & Fractals , 2007, 32 (4) : 1530–1537. |
| [20] | Liu Y, Wang Z, Liang J, et al. Synchronization and state estimation for discrete-time complex networks with distributed delays[J]. IEEE Transactions on Systems, Man, Cybernetics, Part B:Cybernetics , 2008, 38 (5) : 1314–1325. DOI:10.1109/TSMCB.2008.925745 |
| [21] | Boyd S, Ghaoui L E, Feron E, et al. Linear matrix inequalities in system and control theory[M]. Philadelphia, PA, USA: SIAM , 1994 . |



