1 引言
从日常使用的家用电器到工业领域中的各种大型机电装备系统,从简单的电子控制系统到高科技含量的计算机、深海探测系统和航空航天系统,故障无处不在[1].导致故障发生的原因多种多样,如系统设计本身存在的缺陷、制造或实施过程中的错误、不可避免的磨损、外来的恶意攻击及干扰、人为操作不当等.可以说,只要系统运行,故障的发生就是不可避免的[2].
随着科学技术的不断发展,系统的自动化、集成化、智能化程度越来越高,一旦某个模块出现故障而又未能及时发现和排除,就可能会造成整个系统的瘫痪,造成经济损失并危及人的生命安全[3-4].同时,现代系统对人的依赖程度越来越低,很多系统完全脱离人的控制,如火星探测器、深海探测仪及各种用于特殊行业的机器人,一旦这些系统发生故障,传统的基于故障诊断与预测的事后维修方式将无法适用[5].
为了从根本上解决装备系统的故障诊断和修复问题,研究人员不断地对常规方法进行改进,并提出新的思路,系统自愈思想就是在这样一种大环境下应运而生的[6-7].为此,国内外学术界和工业界人士围绕故障监测、诊断和维修等方面开展了大量的研究和实践工作[8-9].在1997年美国提出的展望2010年下一代制造计划中,将自修复(self-repair)和自维修(self-maintenance)技术列为研究重点之一[10]. 2002年美国在面向下一代国防需求的材料研究中将军用装备的自修复材料研究列为提升装备性能的关键技术之一[11]. 2007年,美国伊利诺伊大学航空工程学教授斯科特·怀特研制成功了迄今为止第一种具备自我修复、具有“自愈”能力的新材料,可望解决复合材料出现细微裂纹构成安全隐患的问题[12].日本曾经将汽车的自修复材料列为本国的研究重点[13-14],其目标是实现汽车不同部位材料都具有自修复功能(包括外部壳体和窗户材料、内部装饰材料、轮胎、车轴及发动机等).
文[15-16]将人工智能理论和故障自愈理论相结合,以故障的消除和抑制为目的,从系统内部出发,建立基于免疫原理的故障自愈系统模型,探讨故障智能自愈的理论与方法,提高系统对动态环境的适应性和对不完全信息的处理能力,使系统具有自诊断、自恢复功能,以实现系统内在的自愈保护[17].
机电装备信号调理系统的故障诊断方法有很多,如BP(back propagation)神经网络、专家系统、模糊理论、粗糙集、支持向量机等[18].由于不仅仅考虑信号调理系统的故障诊断,还要考虑其后的系统自愈,所以更多地考虑人工免疫系统[19].关于自愈系统的定义有很多,通过对各个定义判定,较为被认可的一个定义如下:在系统运行过程中,能够自行感知系统运行环境和系统内部状态的变化;在期望的时间内,通过系统微单元之间信息的传递及协调,对系统局部的、早期的失效形式和故障实现自诊断,经优化决策后启动有效恢复机制的,具有免疫认知能力的系统[20].
对信号调理系统的结构特点、参数特性及典型的故障特征等进行分析,并建立健康因子群对系统的抗衰性能进行评估.建立自愈系统与免疫系统映射关系,构建基于免疫原理的故障自愈系统结构模型并给出模型中主要模块结构和实现算法.根据系统故障自愈模型建立的方法,建立信号调理系统的模型,分析系统的故障,并对此模型进行仿真实验,验证故障自愈系统模型的可行性和有效性.经仿真实验证明,基于免疫原理构建的信号调理故障自愈系统,可以实现其主要故障的自愈.
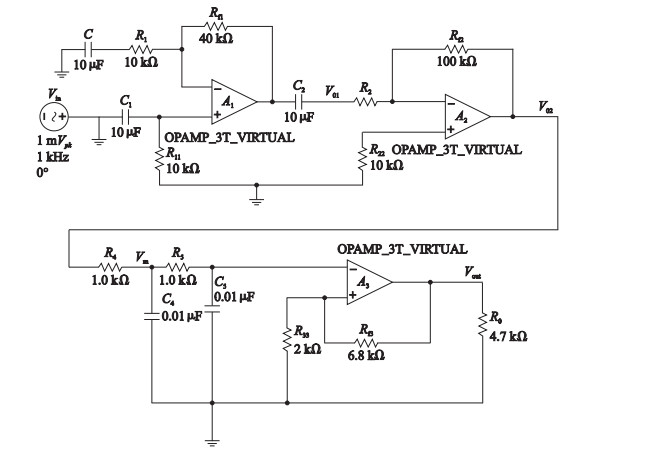
2 信号调理系统及其故障分析 2.1 信号调理系统结构及组成本实验中的信号调理系统由放大电路和滤波电路两个部分组成,图 1给出了系统的具体结构.
|
| 图 1 信号调理系统原理图 Figure 1 Schematic diagram of the signal conditioning system |
(1) 信号调理系统输入的是幅值m在1 mV~50 mV,频率f在600 Hz~1 kHz范围内的信号;
(2) 对(1)中输入的信号,经处理后可以有效放大A=220倍,实际放大倍数与理论计算值的偏差应小于10%;
(3) 当信号调理系统的输入信号f>1.5 kHz时,系统将会以40 dB/dec的幅度衰减;
(4) 经信号调理后,输出信号与输入信号的相位相差180°,实际相位与理论值的偏差应小于8°.
2.1.2 信号调理系统工作原理图 1中,放大电路放大倍数A12满足:
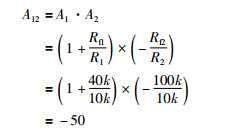
|
(1) |
信号调理系统的滤波电路是由R4、C4、R5、C5和A3组成的,由此可得滤波电路上限截止频率fc为
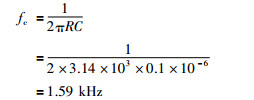
|
(2) |
滤波电路频率信号的放大倍数A3为
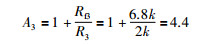
|
(3) |
则电路总放大倍数A为
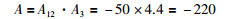
|
(4) |
此信号调理系统的信号放大倍数A=220且f>1.59 kHz的信号将会以40 dB/dec倍频大幅衰减.
2.2 系统主要故障分析基本的信号调理系统是由放大电路和滤波电路两部分组成.在进行仿真之前,先对这两个电路的故障进行分析.
2.2.1 放大电路放大电路通常由信号源、放大器、负载等组成,对放大电路的组成进行分析,放大电路常见故障如表 1所示.
| 序号 | 故障原因 | 故障现象 |
| 1 | 负反馈回路电阻值变化 | 放大倍数变化 |
| 2 | 负反馈电阻开路 | 饱和失真,开环放大,A剧增 |
| 3 | 负反馈电路短路 | 放大器失去放大作用,A=1 |
| 4 | 电源电压值波动 | 输出非线性失真,放大倍数下降 |
| 5 | 集成运算放大器芯片性能下降 | 输出失真,放大倍数下降 |
| 6 | 电源电压的内阻过大 | 放大器的低频自激振荡 |
| 7 | 干扰信号逐级传播放大 | 输出信号被淹没 |
系统的滤波电路由2个RC电路及1个负反馈放大电路组成,滤波电路的主要故障如表 2所示.
| 序号 | 故障原因 | 故障现象 |
| 1 | 某一滤波电容开路 | 对高频信号的衰退率下降,信号相位差减小 |
| 2 | 滤波电容全部开路 | 丧失滤波功能 |
| 3 | 滤波电容短路 | 信号输出为0 |
通过对以往资料的的查询可以得到常见故障的故障率如表 3所示.根据上面的3个表格可以看出系统中常出现的故障及一些故障发生的概率,本文对这些信息进行收集处理,把各种故障看成抗原,针对这些故障的自愈策略当作抗体,把它们存放在固有免疫应答模块,当系统检测到这些故障时,可以迅速的调取自愈策略来处理.在仿真实验中,主要考虑系统的以下3种故障:
| 电阻 | 电容 | 运算放大器 | |
| 参数变化 | 36% | 13% | - |
| 开路 | 59% | 16% | - |
| 短路 | 5% | 73% | - |
| 性能下降 | - | - | 5% |
(1) 反馈电阻开路(如Rf1开路);
(2) 放大倍数下降(如A2下降);
(3) 滤波电容短路(如C4短路).
3 信号调理故障自愈系统设计 3.1 状态特征量选取及编码方式当进行自愈系统设计时,首先考虑信息处理模块,因为在这个模块会进行数据采集与预处理、对状态特征进行提取与编码.
首先对信号调理系统的状态信号Vin、Vout及Vo1、Vo2、Vm这几个节点的数据进行采集,把信号调理系统的两个放大电路的放大倍数A1、A12和总的放大倍数A、电压Vm及信号相位差Δθ作为系统状态特征量,系统状态特征编码用s来表示:
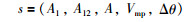
|
(5) |
其中,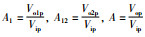
通过信息处理模块对采集数据的处理及特征提取,在状态评估模块对系统的运行状态进行量化的评估,具体方法为:
将信号调理系统的健康因子群用式(6)表示:
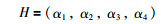
|
(6) |
其中,α1、α2、α3、α4分别为A1、A2、Vm和Δθ的衰退值.
3.3 系统检测器集的生成信号调理系统的自愈系统在完成对系统状态的量化后,需要在自己/非己模块中进行识别,这需要根据已知的数据来生成系统的检测器集.系统采用了阴性选择算法来提高系统检测器的覆盖率,具体步骤为:
对信号调理系统正常与故障运行时采集到的数据进行归一化处理.从这些数据中选取10组自己样本(见表 4),用于系统准检测器集的训练.针对3类已知故障,选取15组故障样本,每类故障5组样本(见表 5),用于训练已知故障检测器子集.
| 样本 | 系统状态特征量 | ||||
| A1 | A12 | A | Vm | Δθ | |
| 1 | 0.010 | 0.112 | 0.502 | 0.042 | 0.966 |
| 2 | 0.010 | 0.110 | 0.494 | 0.041 | 0.960 |
| 3 | 0.009 | 0.110 | 0.504 | 0.041 | 0.965 |
| 4 | 0.010 | 0.113 | 0.503 | 0.042 | 0.949 |
| 5 | 0.010 | 0.111 | 0.500 | 0.041 | 0.962 |
| 6 | 0.009 | 0.112 | 0.503 | 0.041 | 0.960 |
| 7 | 0.009 | 0.112 | 0.502 | 0.042 | 0.960 |
| 8 | 0.010 | 0.111 | 0.495 | 0.042 | 0.955 |
| 9 | 0.009 | 0.111 | 0.502 | 0.041 | 0.956 |
| 10 | 0.009 | 0.112 | 0.503 | 0.042 | 0.959 |
| 样本序号 | 故障类型 | 系统状态特征量 | ||||
| A1 | A12 | A | Vm | Δθ | ||
| 1 | 反馈电阻Rf2开路 | 1.000 | 1.000 | 1.000 | 0.999 | 0.687 |
| 2 | 1.000 | 1.000 | 1.000 | 0.986 | 0.589 | |
| 3 | 1.000 | 1.000 | 1.000 | 1.000 | 0.663 | |
| 4 | 1.000 | 1.000 | 1.000 | 1.000 | 0.658 | |
| 5 | 1.000 | 1.000 | 1.000 | 0.999 | 0.646 | |
| 6 | 放大倍数A2变化,Rf2变化范围在(>10 k) | 0.009 | 0.099 | 0.441 | 0.037 | 0.942 |
| 7 | 0.009 | 0.101 | 0.454 | 0.038 | 0.966 | |
| 8 | 0.010 | 0.103 | 0.462 | 0.038 | 0.955 | |
| 9 | 0.009 | 0.107 | 0.471 | 0.040 | 0.963 | |
| 10 | 0.009 | 0.108 | 0.484 | 0.039 | 0.950 | |
| 11 | 滤波电容C4短路 | 0.009 | 0.111 | 0.000 | 0.000 | 0.990 |
| 12 | 0.009 | 0.110 | 0.000 | 0.000 | 0.988 | |
| 13 | 0.010 | 0.112 | 0.000 | 0.000 | 0.981 | |
| 14 | 0.009 | 0.111 | 0.000 | 0.000 | 0.988 | |
| 15 | 0.009 | 0.112 | 0.000 | 0.000 | 0.989 | |
对阴性选择算法参数设置如下:训练进化代数iter=50,准检测器规模为N=80,匹配阈值δm=0.84,克隆个数为c1=10,变异率vh=0.2,相似度阈值δr=0.96,自然死亡阈值δd=0.6,共L=3类已知故障,每类故障样本数R=3.利用Matlab对改进的阴性选择算法进行编程,然后将由阴性选择算法得到训练数据样本存放到检测器中.其中,3类已知故障检测器子集Mk1、Mk2、Mk3中检测器的数目分别为9个、7个和8个;对其检测器进行聚类,可以得到6个未知故障类检测器子集[8].
3.4 各数据库设计在故障自愈系统模型中,其中一个非常重要的部分就是各种数据库的搭建,包括存放着已知故障的抗原库、与这些已知故障对应的自愈策略的抗体库.在本次实验中搭建为:
(1) 信号调理系统常见故障存放在系统的已知抗原库里,本实验中对于未知故障的学习后得到故障也存在此抗原库.故本实验中已知抗原库中抗原的个数为15个.
(2) 系统进行自愈时的自愈响应都在自愈策略库中.自愈响应根据系统中具体故障的具体特点来响应.在此次实验中,对系统设计的4个自愈响应进行编码,见表 6.
| 序号 | 编码 | 自愈动作 |
| 1 | 001 | 调节反馈电阻Rf2阻值 |
| 2 | 010 | 闭合开关K1 |
| 3 | 011 | 闭合开关K2 |
| 4 | 100 | 启动滤波程序 |
(3) 用二进制编码方式对抗体编码.抗体即自愈策略存放在记忆抗体库中.在此次实验中已知抗原有3类,因此相应的记忆抗体也有3种.针对表 6中4个自愈响应因此抗体的也是由4个码段进行编码,对应4个自愈响应.记忆抗体库如表 7所示.
| 编码 | 自愈策略 |
| 00 00 001 010 000 000 | 闭合开关K1,调节Rf2阻值(功能冗余) |
| 00 01 001 000 000 000 | 调节Rf2阻值(补偿) |
| 00 10 000 000 011 100 | 闭合开关K2,启动滤波程序(功能冗余) |
仿真实验由Multisim软件对信号调理系统的特性及故障进行分析,在Protues软件环境下实现故障自愈系统的实时监测与仿真;由手动方式引入各种可恢复故障(包括已知故障和未知故障).如果系统能够在无人干预的情况下,正确地识别出故障类型,并通过执行适当的自愈策略使系统运行由异常状态恢复到正常状态,则认为该故障自愈系统模型是可用且有效的.
首先,单片机实现信号调理系统的状态检测,通过虚拟串口实现单片机与计算机的串行通讯;其次,将检测到的状态送入Matlab环境下编写的自愈程序;最后,将自愈程序的决策结果回送给单片机,进行自愈策略的执行,从而实现系统故障自愈过程.
系统硬件部分的工作原理如图 2所示.其中,单片机定时对信号调理电路检测点的信号进行采集,经A/D转换后得到相应的数字量,送到计算机,判断检测到的系统状态是否正常,启动免疫自愈机制,匹配得到相应的自愈策略;再由单片机将自愈指令经D/A转换为模拟调节量或将控制信号直接作用于信号调理系统,实现系统故障的自诊断和自恢复.

|
| 图 2 系统工作原理图 Figure 2 System′s working principle diagram |
为了验证故障自愈系统模型的可行性和有效性,在仿真中,系统初始运行状态为正常状态,当系统运行一段时间后,进行5组仿真实验:
实验1 无动作,获取时间t之后的第1个检测状态(当t=12 s时)进行识别;
实验2 手动断开与反馈电阻Rf1串联的开关KF1,研究已知故障1;
实验3 手动调节可调电路Rf0,实现反馈电阻阻值的变化,研究已知故障2;
实验4 手动闭合开关KF2,实现电容C4的短路,研究已知故障3;
实验5 手动闭合开关KF3,实现电容C5的短路,研究未知故障.
为了方便研究,在实验中均采用单一频率的信号作为输入信号.因此,在1~3组实验中,输入信号为10 mV、600 Hz的正弦信号;在4、5组实验中,选用1 mV、2.5 kHz的正弦信号作为输入信号,研究滤波电路对高频信号的衰减作用.
4.1 仿真系统硬件设计仿真系统硬件的设计是在Protues软件环境下进行的.硬件电路是由信号调理电路、单片机数据采集、自愈执行机构和上位机等组成.
信号调理电路中,Rf2采用可编程数字电位器芯片CAT511与可调电阻Rf0串联组成,通过单片机输出控制CAT511芯片的实际阻值,实验反馈电阻Rf2阻值可调,电阻Rf0用于引入故障;数据采集部分由定时器T0和中断控制实现5路数据的巡回采集,每2 s采集一次,每次采集5路数据,数据采集选用12位A/D转换器AD1674,采样频率为5.12 kHz;A/D转换的量和为双极性-5.000 0~+5.000 0,5路信号的输入范围不同,为了取得较好的转换效果,对5路输入信号进行不同的放大,以实现满量程转换;开关K1、K2由单片机驱动继电器动作实现;在这里为简化研究,直接将示波器与信号调理电路的检测点相连,观察系统故障自愈效果.
4.2 仿真系统软件设计信号调理系统故障自愈的软件由两部分组成:
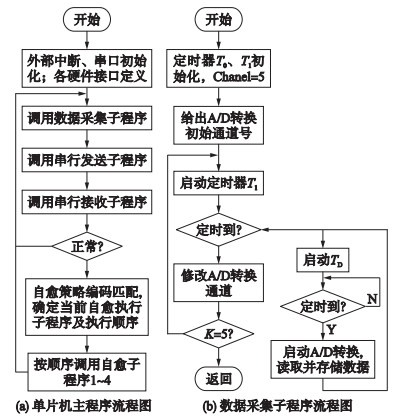
(1) 单片机控制程序由主程序和数据采集子程序、自愈策略执行子程序、串行通讯子程序等构成,实现对5个检测点信号的采集和故障自愈策略的执行,通过Keil-C51与Protues进行联调. 图 3给出了主程序和数据采集子程序的流程图.
|
| 图 3 部分单片机程序流程图 Figure 3 Part of the MCU program flow chart |
(2) 故障自愈程序是在计算机中Matlab环境下运行的故障自愈程序,完成系统检测器的生成、系统状态识别和自愈策略的生成,单片机与上位机由虚拟串口进行通讯.
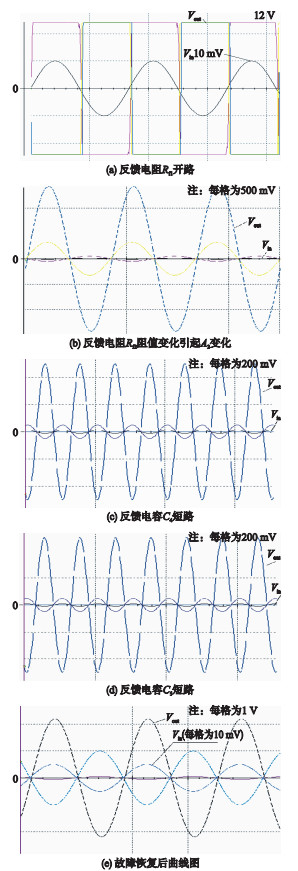
5 仿真结果分析在实验中,分别将Rf1开路、Rf2阻值偏移、C4短路和滤波电容C5短路四种不同故障引入信号调理故障自愈系统中,图 4给出4种故障发生时示波器显示曲线.可以看到,滤波电容C4与C5短路对检测点Vo1、Vo2和Vout有相同的故障响应曲线,但反映到系统状态特征量上,两者是可以区别的.
|
| 图 4 仿真响应曲线 Figure 4 Simulation response curves |
通过基于免疫原理的故障识别与自愈调节,上述4种故障均可以恢复,系统能够在允许的误差范围完成放大、滤波功能. 表 8给出了各故障的自愈过程.
| 序号 | 故障类型 | 检测状态量 | 激活检测器数目 | 隶属度 | 抗原(编码) | 抗体(编码) |
| 1 | 0(无故障) | (0.009 0.114 0.499 0.042 0.966) | [0 0 0 0 0 0 0 0 0] | [0 0 0 0 0 0 0 0 0] | - | - |
| 2 | 1 | (1.000 1.000 1.000 1.00 0.688) | [9 0 0 0 0 0 0 0 0] | [0.113 0 0 0 0 0 0 0 0] | (11 00 1.000 1.000 1.000 1.000 0.688) |
(11 00 001 010 000 000) |
| 3 | 2 | (0.009 0.078 0.347 0.029 0.966) | [0 8 0 0 0 0 0 2 0] | [0 0.100 0 0 0 0 0 0.025 0] | (01 01 0.009 0.078 0.347 0.003 0.966) |
(01 01 001 000 000 000) |
| 4 | 3 | (0.009 0.111 0.000 0.000 0.990) | [0 0 7 0 1 0 0 1 0] | [0 0 0.088 0 0.013 0 0 0.013 0] | (11 10 0.009 0.111 0.000 0.000 0.990) |
(11 10 000 000 011 100) |
| 5 | 未知故障 | (0.009 0.112 0.000 0.025 0.994) | [0 0 4 0 0 0 1 0 0] | [0 0 0.05 0 0 0 0 0.136 0 0] | (11 11 0.009 0.112 0.000 0.003 0.996) |
(11 01 000000 011 100) |
对5组实验结果进行分析:
实验1中的系统状态检测为正常状态,不采取任何自愈策略,故障自愈系统返回指令为:等待下一次数据采集结果.
实验2~5,按照8表所述完成自愈过程,通过执行与抗体编码相对应的自愈策略,使系统从故障状态恢复到正常运行状态.其中,实验2~4的已知故障可以很好地与记忆抗体进行匹配,具有较好的自愈效果:实验2中的故障采用组合自愈策略,首先切除故障组件Rf1,然后重新分配两级放大器的放大倍数,第1级放大器组成跟随器,即A1=1,通过调整Rf2阻值,使得A12=A2=50,实现故障自愈;实验3中,根据补偿思想设计自愈策略,通过调节Rf2阻值消除偏差,恢复原放大倍数;实验4中验证了基于软/硬件替换的自愈策略,通过调用软件滤波程序,恢复信号调理系统的滤波功能.
实验5为未知故障,通过计算其与已知抗原的相似度,可以找到唯一的最相似已知抗原(0.009 2,0.112 2,0.000 0,0.000 0,0.989 3),按照该已知抗原的方法处理未知故障,实验证明该策略可以有效地实现未知故障的自愈.经过该实验后,故障自愈系统在检测间歇启动学习记忆功能,将该未知故障状态加入已知抗原库,同时更新了系统检测器集.将与该未知抗原相匹配的检测器加入其最相似已知故障检测子集Mk3.
从上述实验中可以看到,本文设计的故障自愈系统具有可行性和有效性,能够较准确地识别状态并为故障匹配合适的自愈策略.
从以上5个实验可以看出,本文基于免疫原理的信号调理系统故障自愈系统能够及时识别自己/非己状态,并针对故障及时的调用自愈策略来对故障进行自愈处理.这说明这个自愈策略是行得通的.
6 结论本文以信号调理系统为对象,构建基于免疫原理的故障自愈系统.研究3种典型故障(反馈回路开路、放大倍数偏移及滤波电容击穿的自愈)及1种未知故障.根据故障及系统结构特点,制定相应的自愈策略,实验表明这些自愈策略对故障具有较好的恢复效果.论文中仅以信号调理系统为例验证了模型的可行性,其故障多属于硬件可恢复故障,对于模型在其他类型的系统及软件故障方面的有效性还有待进一步的研究与完善.
| [1] | 蔡静文, 胡军, 何金良, 等. 含微网的智能配电网故障自愈过程中操作过电压特征[J]. 电网技术 , 2013 (9) : 2615–2620. CaiJ W, Hu J, HeJ L, et al. Characteristics of switching overvoltage in smart distribution network containing microgrid during fault self-healing process[J]. Power System Technology , 2013 (9) : 2615–2620. |
| [2] | 许海云. 机电设备绿色维修技术探讨[J]. 设备管理与维修 , 2012 (11) : 38–39. Xu H Y. The discussing of green maintenance technology about mechanical and electrical equipment[J]. Plant Maintenance Engineering , 2012 (11) : 38–39. |
| [3] | 杨晶, 任光俊, 王耀清, 等. 煤矿机电设备故障分析及预防措施研究[J]. 科技创新导报 , 2013 (3) : 95, 97. Yang J, Ren G J, Wang Y Q, et al. Coal mine mechanical and electrical equipment failure analysis and prevention measures research[J]. Science and Technology Innovation Herald , 2013 (3) : 95, 97. |
| [4] | 曹建福, 曹雯. 基于改进证据理论的大型制造装备故障诊断[J]. 振动、测试与诊断 , 2012, 4 (4) : 532–537, 684. Cao J F, Cao W. Large manufacturing equipment fault diagnosis based on evidence theory[J]. Journal of Vibration, Measurement & Diagnosis , 2012, 4 (4) : 532–537, 684. |
| [5] | 王维民, 高金吉, 李燕, 等. 离心压缩机轴位移故障自愈调控系统试验研究[J]. 机械工程学报 , 2010, 46 (5) : 49–54. Wang W M, Gao J J, Li Y, et al. Experimental study about centrifugal compressor axial displacement fault self-recovering system[J]. Journal of Mechanical Engineering , 2010, 46 (5) : 49–54. DOI:10.3901/JME.2010.05.049 |
| [6] | 吴静子, 魏登峰. 基于改进粒子群算法的配电网故障自愈算法[J]. 电力学报 , 2014 (3) : 206–210, 222. Wu J Z, Wei D F. Distribution network fault self-healing algorithm based on improved particle swarm optimization algorithm[J]. Journal of Electric Power , 2014 (3) : 206–210, 222. |
| [7] | 仇慧娟, 张广明. 基于免疫Agent机电装备故障智能自愈系统建模[J]. 计算机工程与设计 , 2011, 32 (10) : 94–98. Qiu H J, Zhang G M. Modeling of mechanical and electrical self-healing system based on immune agent[J]. Computer Engineering and Design , 2011, 32 (10) : 94–98. |
| [8] | 周娟娟, 张广明, 袁宇浩. 基于免疫Agent的风力发电机组故障自愈系统的研究[J]. 机械设计与制造 , 2012 (3) : 136–138. Zhou J J, Zhang G M, Yuan Y H. Study of fault self-healing system for wing turbine based on immune-agent[J]. Machinery Design & Manufacture , 2012 (3) : 136–138. |
| [9] | 刘慧芳.智能配电网故障自愈技术研究[D].天津:天津大学, 2014. Liu H F. Intelligent power distribution network fault self-healing technology research[D]. Tianjin:Tianjin University, 2014. http://cdmd.cnki.com.cn/article/cdmd-10056-1015019508.htm |
| [10] | Zhou W, Liu Y J, Cao Q F, et al. Fault diagnosis of engine based on improved dempster-shafer information fusion method[J]. Applied Mechanics and Materials , 2009 (16) : 1310–1317. |
| [11] | Fan X F, Zuo M J. Fault diagnosis ofmachines based on D-S evidence theory, part 1:D-S evidence theory and its improvement[J]. Pattern Recognition Letters , 2006, 27 (5) : 366–376. DOI:10.1016/j.patrec.2005.08.025 |
| [12] | Fan X F, Zuo M J. Fault diagnosis ofmachines based on D-S evidence theory, part 2:Application of the improved D-S evidence theory in gearbox fault diagnosis[J]. Pattern Recognition Letters , 2006, 27 (5) : 377–385. DOI:10.1016/j.patrec.2005.08.024 |
| [13] | Sterrit R. Autonomic networks:Engineering the self-healing property[J]. Engineering Applications of Artificial Intelligence , 2004, 17 (7) : 727–739. DOI:10.1016/S0952-1976(04)00111-3 |
| [14] | Boukerche A, Machado R B, Jucá K R L, et al. An agent based and biological inspired real-time intrusion detection and security model for computer network operations[J]. Computer Communications , 2007, 30 (13) : 2649–2660. DOI:10.1016/j.comcom.2007.03.008 |
| [15] | 曹志高. 基于Web机电装备故障诊断系统体系研究[J]. 现代机械 , 2010 (3) : 91–94. Cao Z G. Electrical and mechanical equipment fault diagnosis system research based on the Web[J]. Modern Machinery , 2010 (3) : 91–94. |
| [16] | Zhu J, Shi D. A possible self-healing mechanism in damaged graphene by heat treatment[J]. Computational Materials Science , 2013, 68 (2) : 391–395. |
| [17] | Montani S, Anglano C. Self-healing in service deli-very software systems by means of case-based reasoning[J]. Engineering Applications of Artificial Intelligence , 2006, 42 (1) : 5–18. |
| [18] | 高春甫, 艾学忠. 微机测控技术[M]. 北京: 科学出版社 ,2005 . Gao C P, Ai X Z. Microcomputer measurement and control technology[M]. Beijing: Science Press , 2005 . |
| [19] | 高鹏. 10 kV架空分支线路故障自愈控制方案研究[D].淄博:山东理工大学, 2013. Gao P. Branch of 10 kV overhead line fault self-healing control system research[D]. Zibo:Shandong University of Science and Technology, 2013. |
| [20] | Debanjan G, Sharman R. Self-healing systems-Survey and synthesis[J]. Decision Support Systems , 2007, 42 (4) : 2164–2185. DOI:10.1016/j.dss.2006.06.011 |



