1 引言
过程数据分析的一个主要任务是从经验或历史数据中建立回归模型并用于产品的质量预测.当前常用的多变量统计回归预测方法如主元回归(PCR)[1-2]、偏最小二乘回归(PLSR)[3]等都属于基于主成分的分析方法,有效处理了工业过程中变量较多且耦合严重的现象,在过程建模、监控等领域应用广泛[4-5].但这些方法在建模时都需假定测量数据是满足独立同分布的高斯变量,提取的主成分仅仅满足非相关而非独立,不能充分利用过程数据的高阶特性,因此对那些工业数据中出现的非高斯数据表现欠缺.独立成分分析(ICA)[6-8]作为近年来快速发展起来的一种新的统计信号处理方法,正是以数据非高斯分布为前提的,提取的独立成分满足统计意义上的独立性特点,具有高阶统计特性,可以携带更深层次的结构和分布更多的信息.长期以来,各种基于ICA的多变量统计方法被用于过程监控,如核ICA[9]、局部ICA[10]以及多向ICA[11]等.随后,基于ICA建立回归模型用于质量预测的方法也逐渐发展起来.其中一些较为经典的如独立成分回归(ICR)[12]、基于ICA的多元线性回归(ICA-MLR)[13]以及基于ICA的偏最小二乘回归(ICA-PLSR)[14]等.由于独立成分回归方法具有诸多优点,近年来很多复杂的扩展的独立成分回归方法也被提出并加以利用,如文[15]提出的结合概率的局部独立成分回归方法,通过引进贝叶斯推断策略,分别计算出不同操作模态的数据样本的后验概率,然后建立不同模态的局部ICR模型,用于化工过程的多模态质量预测.以及文[16]提出的基于统计数据分析与校正模型的多重集独立成分回归(MsICR)方法和文[17]提出的集成独立成分回归(ensemble ICR)方法等.这些改进算法使得基于独立成分分析的回归算法在实际过程中的应用更为广泛和有效.
通常,在多变量过程数据X中都会含有与目标变量Y不相关的统计变化.因此,在ICA利用负熵理论来提取高阶统计量时也会提取到无关的干扰成分[18],该部分变化对质量变量的预测毫无作用.从数学意义上讲,X中与Y无关的信息必定与Y正交.基于这个思想,Wold等[19]提出了正交信号校正(orthogonal signal correction,OSC)算法,以去除X中跟Y正交的信息.在此基础上,Trygg和Wold提出了基于非线性迭代偏最小二乘(NIPALS)算法的正交PLS(O-PLS)算法[20].从本质上说,O-PLS算法是一种数据预处理方法,将数据X中和Y无关的成分滤除.对于被过滤数据X的PLS回归建模能够得到更为简单有效的模型.根据前面内容所述,PLS方法在非高斯过程的应用中存在局限性,因此,当多变量过程数据呈现非高斯性时,应用O-PLS也得不到理想的预处理效果.
鉴于此,本文提出一种适用于非高斯过程的信号校正方法,即在ICA算法的基础上,结合OSC方法对其进行改进,建立正交独立成分分析(O-ICA)算法,以去除ICA在提取高阶统计量时带来的干扰变化.再对被校正后的X提取独立成分,并以其为自变量,Y为应变量建立多元线性回归(MLR)预测模型——正交独立成分回归(orthogonal independent component regression,O-ICR).最后将本文提出的方法应用到Tennessee Eastman(TE)过程的质量预测仿真中,并与传统的ICR方法进行比较,验证该方法在回归预测方面性能的有效性.
2 ICA简介ICA算法目的是把观察到的数据进行某种线性分解,使其分解为相互独立的成分分量. Jutten和Herault[6]最早提出ICA概念,并给出了ICA一种简单的描述,认为ICA是从线性混合信号里恢复出一些基本源信号的方法.
设输入数据阵X∈Rd×n.其中,d为样本数,n为变量个数.则X可分解为
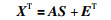
|
(1) |
其中,A∈Rn×m,E∈Rd×n为误差矩阵,独立成分矩阵S=[s1,s2,…,sd],可表示为

|
(2) |
其中,W为分离矩阵.对于ICA算法提取的源信号,其非高斯性可以用基于峰度值或负熵值等方法测量.本文采用目前较为成熟的基于负熵最大的快速固点算法(FastICA)[21]求取分离矩阵W,再获得源信号S的估计值.
3 O-ICR方法引言中已经分析了在ICA利用负熵理论来提取高阶统计量时会提取到与Y无关的干扰成分,该部分变化会影响最终质量变量的预测精度.同时,考虑到OSC算法的基本思想:当使过程变量X与质量变量Y相关时,提前剔除自变量中那些与因变量相关性较小甚至不相关的数据信息.本文提出一种新的预处理方法——正交独立成分分析(O-ICA)算法.在ICA算法的基础上,结合Wold等[19]提出的OSC方法进行改进,用于非高斯过程的信号校正.并将预处理过的过程变量矩阵XO与质量变量矩阵Y组合为新的数据阵{XO,Y},代入线性ICR算法以建立回归模型,求取模型回归系数,得到最终的质量预测结果.
下面将详细介绍正交独立成分分析(O-ICA)算法步骤,以及基于O-ICA的回归建模方法O-ICR.
3.1 O-ICA预处理假设原输入输出矩阵X和Y(n×1)已标准化,具体方法步骤如下:
(1) 对X进行ICA分解,得到独立成分S;
(2) 初始化正交成分的得分向量t⊥:t⊥←s,其中s是S的第1行,作为正交成分得分向量的起始值,这样t⊥就包含了X中较大的系统变化信息;
(3) 计算tnew=t⊥-Y(YTY)-1YTt⊥,显然:YTtnew=YT(t⊥-Y(YTY)-1YTt⊥)=YTt⊥-YTY(YTY)-1YTt⊥=0,tnew与Y正交;
(4) 将X作为自变量,tnew作为因变量,计算权重向量w,令其满足:Xw=tnew;
(5) 通过X与w计算新的得分向量t⊥:t⊥=Xw.此时得到的新的t⊥与初始化时的tnew不一定相等,因此,不一定和Y正交.重复步骤(3)~(5)直到t⊥收敛,这样,得到的t⊥不仅和Y正交,而且能从X直接得到;
(6) 计算正交成分的负载向量p⊥:p⊥=XTt⊥/(tTt⊥);
(7) 对X进行校正,过滤掉X中与Y正交的干扰信息,得到XO:XO=X-t⊥p⊥T.
如需除去更多的正交正分,可用XO代替X,重复步骤(1)~(7).
3.2 O-ICR预测上节已对原始输入数据X进行非高斯过程的信号校正,获得无干扰变化的输入数矩阵XO.本节将继续对XO进行ICA分解,得到新的独立成分S,代替原输入数据与Y进行MLR建立回归预测模型:

|
(3) |
式中,B为回归系数,可用最小二乘法[3]通过下式获得:

|
(4) |
由此可得到训练样本和测试样本的回归预测值分别为
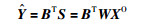
|
(5) |
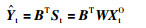
|
(6) |

|
(7) |
式中,XtO为Xt进行O-ICA校正后的输入矩阵,H表示过程变量矩阵X与输出变量矩阵Y之间的回归系数.
具体的O-ICR预测方法按图 1设计,主要分为3步:

|
| 图 1 O-ICR预测方法流程图 Figure 1 Illustration of the O-ICR method |
(1) 在训练模块,输入训练组数据X、Y,对其执行O-ICA算法以获得修正后的输入数据阵XO.再对XO执行ICA算法并按式(2)提取独立成分矩阵S和对应的分离矩阵W.
(2) 将S和Y按式(4)计算回归系数B,并以S为自变量,B为回归系数建立MLR模型,按式(5)计算出训练组的输出预测值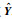
(3) 在测试模块,输入测试组Xt,对其执行O-ICA算法获得修正后的XtO,再按式(2)计算得到独立成分矩阵St.然后以St为自变量,由离线建模得到的B为回归系数,执行MLR模型按式(6)计算得到最后的预测输出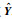
此外,为了比较模型的回归预测能力,本文采用以下三种性能评判指标:
(1) 均方根误差ERMSE:
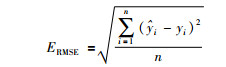
|
(8) |
式中,yi为实际值,
(2) 平均绝对误差EMAE:
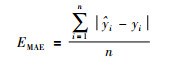
|
(9) |
式中,yi为实际值,
(3) 复测定系数R2:
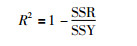
|
(10) |
式中,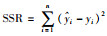

本节将本文提出的方法应用于TE过程的质量预测中,并与传统的ICR方法进行对比,验证该方法的有效性.为了公平对比各模型的预测性能,仿真过程中每种模型的训练集和测试集以及挑选的独立成分的个数都是相同的.
4.1 TE过程简介及实验数据选取Tennessee Eastman(TE)过程是一个典型的多变量复杂化工生产过程,目前已被广泛作为控制算法的测试和性能评估的仿真平台[22-23].该过程系统主要由5个操作单元组成,分别为:连续搅拌式反应釜、冷凝器、气液分离塔、汽提塔和离心式压缩机.共包括12个操纵变量、22个连续过程测量变量和19个非连续测量成分变量.仿真过程中采样间隔均为3 min.本实验选取的训练集和测试集分别为两组正常数据,每组数据包含500个采样点.训练集用来建立模型,测试集用来验证模型.为了获得较好的预测效果,首先利用PLS算法对TE过程的11个操纵变量和22个连续测量变量进行回归分析,挑选其中预测结果满足性能指标R2>0.7且拟合较好的5个测量变量作为本文的预测输出.具体的输入输出实验数据选取结果见表 1.
| symbol | variables | unit |
| x1 | 物流A进料量 | kmol/h |
| x2 | 物流D进料量 | kmol/h |
| x3 | 物流E进料量 | kmol/h |
| x4 | 物流A、C总进料量 | kmol/h |
| x5 | 压缩机回收阀开度 | % |
| x6 | 排放阀开度 | % |
| x7 | 分离器罐液流量 | kmol/h |
| x8 | 汽提器液体产品流量 | kmol/h |
| x9 | 汽提器水流阀 | % |
| x10 | 反应器冷水流量 | m3/h |
| x11 | 冷凝器冷却水流量 | m3/h |
| y1 | 物流A流量 | kmol/h |
| y2 | 放空速率 | r/min |
| y3 | 汽提器液位 | % |
| y4 | 汽提器流量 | kmol/h |
| y5 | 压缩机功率 | kW |
针对实验所选取的输入过程变量与输出质量变量分别建立它们之间的ICR和O-ICR模型. 表 2给出两种方法的预测性能对比结果,表中粗体表示预测结果的最优值.
| model | ERMSE | EMAE | R2 |
| ICR(y1) | 0.088 5 | 0.071 7 | 0.992 2 |
| O-ICR(y1) | 0.067 8 | 0.054 1 | 0.995 4 |
| ICR(y2) | 0.317 1 | 0.254 9 | 0.899 2 |
| O-ICR(y2) | 0.127 6 | 0.102 8 | 0.983 7 |
| ICR(y3) | 0.000 3 | 0.000 3 | 1 |
| O-ICR(y3) | 0.000 3 | 0.000 2 | 1 |
| ICR(y4) | 0.158 5 | 0.127 7 | 0.974 8 |
| O-ICR(y4) | 0.108 4 | 0.084 5 | 0.988 2 |
| ICR(y5) | 0.485 1 | 0.386 9 | 0.764 2 |
| O-ICR(y5) | 0.234 1 | 0.181 9 | 0.945 1 |
对比表 2中的5个质量变量的预测性能指标,可以看出,对于变量y3的预测,两种算法的R2值均为1,都有很好的预测效果.对于变量y2和y5,O-ICR算法的预测性能较ICR算法有明显改善.主要原因是其利用O-ICA对独立信号进行了修正,能够提供更多无干扰的高阶统计信息,更好的反映测量数据的内在特性,所以它得到的回归预测精度较ICR更高.
用O-ICR和ICR方法建模对测试集中5个质量变量的均方根误差见图 2,从图中可以更直观地看出,对于质量变量y3的预测,两种算法的ERMSE值一样小,而对于其余4个质量变量的预测,O-ICR算法比ICR算法的ERMSE更小,表明O-ICR算法的预测能力和回归效果更好.

|
| 图 2 两种方法的均方根误差 Figure 2 ERMSE of two methods |
此外,本实验采用两种方法分别对测试集的5个质量指标进行了预测仿真对比分析.由于文章篇幅所限,下面仅给出对质量变量y2和y5的预测仿真结果,如图 3所示.
由图 3可知,过程变量与质量变量之间可以得到很好的回归效果,这说明基于ICA的回归方法适用于TE过程的建模.此外,通过对比图 3中(a)和(b)的预测结果,可以明显看出,O-ICR算法相对ICR算法更接近实际值,这说明O-ICA作为一种非高斯过程的信号校正方法,有效地去除了ICA在提取高阶统计量时携带的干扰变化,所以经O-ICA算法预处理后得到的独立元,更能本质地描述过程特征,使得基于O-ICA的回归方法O-ICR比传统的ICR取得的预测结果更为理想.

|
| 图 3 两种方法的质量预测结果 Figure 3 Quality prediction results of two method |
本文提出一种新的多元线性回归方法,即正交独立成分回归(O-ICR),用于非高斯过程的质量预测.与传统的基于主成分分析的回归方法相比,该方法提取的独立成分,能有效地利用高阶统计信息,较主成分包含了更多有用的信息;与传统的基于ICA的回归方法相比,该方法去除了ICA在提取高阶统计量时伴随的干扰信息,有效弥补了非高斯数据分布过程中预测精度不足.此外,通过Tennessee Eastman(TE)过程的实验仿真,验证了本文方法应用于过程建模及质量预测的有效性和优越性.
| [1] | Dunteman G H. Principal components analysis[M]. London, UK: Sage Publications , 1989 . |
| [2] | Ge Z Q, Song Z H, Gao F R. Mixture probabilistic PCR model for soft sensing of multimode processes[J]. Chemometrics and Intelligent Laboratory Systems , 2011, 105 (1) : 91–105. DOI:10.1016/j.chemolab.2010.11.004 |
| [3] | Jong S D. SIMPLS:An alternative approach to partial least squares regression[J]. Chemometrics and Intelligent Laboratory Systems , 1993, 18 (93) : 251–263. |
| [4] | Tao E P, Shen W H, Liu T L, et al. Fault diagnosis based on PCA for sensors of laboratorial wastewater treatment process[J]. Chemometrics and Intelligent Laboratory Systems , 2013, 128 (15) : 49–55. |
| [5] | Hu Y, Ma H H, Shi H B. Robust online monitoring based on spherical-kernel partial least squares for nonlinear processes with contaminated modeling data[J]. Industrial and Engineering Chemistry Research , 2013, 52 (26) : 9155–9164. DOI:10.1021/ie4008776 |
| [6] | Jutten C, Heranlt J. Independent component analysis versus PCA[C]//Proceedings of the European Signal Processing Conference. Berlin, Germany:Springer, 1988:287-314. |
| [7] | Hyvarinen A, Oja E. Independent component analysis:Algorithms and Applications[J]. Neural Networks , 2000, 13 (4) : 411–430. |
| [8] | Gan X S, Tang X Q, Gao H L. Modeling method based on smooth support vector regression with independent component analysis feature extraction[J]. Applied Mechanics and Materials , 2015 (713/714/715) : 1773–1776. |
| [9] | Liu Y, Wang F L, Chang Y Q. Reconstruction in integrating fault spaces for fault identification with kernel independent component analysis[J]. Chemical Engineering Research and Design , 2013, 91 (6) : 1071–1084. DOI:10.1016/j.cherd.2012.11.013 |
| [10] | Ge Z Q, Xie L, Kruger U, et al. Local ICA for multivariate statistical fault diagnosis in systems with unknown signal and error distributions[J]. American Institute of Chemical Engineers , 2012, 58 (8) : 2357–2372. DOI:10.1002/aic.12760 |
| [11] | Guo H, Li H G. On-line batch process monitoring with improved multi-way independent component analysis[J]. Chinese Journal of Chemical Engineering , 2013, 21 (3) : 263–270. DOI:10.1016/S1004-9541(13)60485-4 |
| [12] | Shao X G, Wang W, Hou Z Y, et al. A new regression method based on independent component analysis[J]. Talanta , 2006, 69 (3) : 676–680. DOI:10.1016/j.talanta.2005.10.039 |
| [13] | Kaneko H, Arakawa M, Funatsu K. Development of a new regression analysis method using independent component analysis[J]. Journal of Chemical Information and Modeling , 2008, 48 (3) : 534–541. DOI:10.1021/ci700245f |
| [14] | Kaneko H, Arakawa M, Funatsu K. Development of A new soft sensor method using independent component analysis and partial least squares[J]. American Institute of Chemical Engineers , 2009, 55 (1) : 87–98. DOI:10.1002/aic.v55:1 |
| [15] | Ge Z Q, Song Z H, Wang P L. Probabilistic combination of local independent component regression model for multimode quality prediction in chemical processes[J]. Chemical Engineering Research and Design , 2014, 92 (3) : 509–521. DOI:10.1016/j.cherd.2013.09.010 |
| [16] | Zhao C H, Gao F R. Multiset independent component regression(MsICR) based statistical data analysis and calibration modeling[J]. Industrial and Engineering Chemistry Research , 2013, 52 (8) : 2917–2924. DOI:10.1021/ie3023302 |
| [17] | Ge Z Q, Song Z H. Ensemble independent component regression models and soft sensing application[J]. Chemometrics and Intelligent Laboratory Systems , 2014, 130 (2) : 115–122. |
| [18] | Zhang Y W, Teng Y D, Zhang Y. Complex process quality prediction using modified kernel partial least squares[J]. Chemical Engineering Science , 2010, 65 (6) : 2153–2158. DOI:10.1016/j.ces.2009.12.010 |
| [19] | Wold S, Antti H, Lindgren F, et al. Orthogonal signal correction of near-infrared spectra[J]. Chemometrics and Intelligent Laboratory Systems , 1998, 44 (1) : 175–185. |
| [20] | Trygg J, Wold S. Orthogonal projection to latent structures(O-PLS)[J]. Journal of Chemometrics , 2002, 16 (3) : 119–128. DOI:10.1002/(ISSN)1099-128X |
| [21] | Hyvarinen A. Fast and robust fixed-point algorithms for independent component analysis[J]. IEEE Transactions on Neural Networks , 1999, 10 (3) : 626–634. DOI:10.1109/72.761722 |
| [22] | Lau C K, Ghosh K, Hussain M A, et al. Fault diagnosis of Tennessee Eastman process with multi-scale PCA and ANFIS[J]. Chemometrics and Intelligent Laboratory Systems , 2013, 120 (2) : 1–14. |
| [23] | Downs J H, Vogel E F. A plant-wide industrial process control problem[J]. Computers Chemical Engineering , 1993, 17 (3) : 245–255. DOI:10.1016/0098-1354(93)80018-I |



