1 引言
实际工业生产过程中,存在输入变量与输出变量数目不相等的非方系统[1-5].针对非方系统,最简单的处理方法是方形化,即根据性能需求和系统特性,将非方系统转化成方形系统[6-7],再利用方形系统的方法进行设计.由于系统的部分信息被忽略,可能引入右半平面极点致使系统不稳定,因此直接针对非方系统进行控制的策略受到了学者们的推崇[8].另外,由于分散控制具有设计过程简单、鲁棒性能好、能被操作者理解等优点,在非方系统控制理论发展和实际应用中得到广泛研究.如文[9-12]分别利用非方相对增益矩阵法和块相对增益法进行配对,先确定主回路,再针对主回路设计控制器.但是没有考虑来自不同回路的耦合,仅通过配对消弱各通道间的耦合,这样使控制性能有所下降.为了解决上述问题,文[13-14]分别利用非方相对有效增益阵列(NERGA)和非方相对归一化增益阵列(NRNGA)方法,提出基于等价传递函数(ETF)的控制方案.但由于近似化方法的使用,得到的ETF模型精度不高,从而影响了系统的控制性能.
针对上述多变量非方控制系统设计过程中存在的问题,本文提出时滞高维多变量非方系统多环PI控制器设计新方法.考虑来自不同环路的耦合,同时利用ETF与被控过程传递函数广义逆之间的关系建立方程组,推导具有更高精度的ETF解析通式,再结合IMC-PID控制原理,设计多环PI控制器.所提控制方法精度高,适用于高维的多变量非方系统.
2 等价传递函数考虑m×n(m < n)的开环稳定多变量非方系统过程,其闭环分散控制系统结构和等价单输入单输出系统结构如图 1所示,其中ri、ei、yi(i=1,2,…,m)及ui(i=1,2,…,n)分别为参考输入、跟踪误差、系统输出及控制输入,ĝij(i=1,2…,m,j=1,2…,n)为i-j回路的等价传递函数(等价传递函数是指某一回路在其它回路受控闭合后原输入输出之间的开环传递函数),gc,ij(i=1,2…,n,j=1,2,…,m)为对应回路的控制器,G(s)为开环稳定对象的传递函数矩阵:

|
| 图 1 闭环分散控制系统结构和等价单输入单输出系统结构 Figure 1 Closed-loop decentralized control structure and equivalent single-input-single-output control structure |
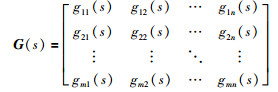
|
根据等价传递函数的性质[14]可知,被控对象的广义逆与等价传递函数存在如下的关系:
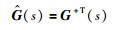
|
(1) |
其中Ĝ(s)、G+(s)分别为被控对象G(s)的对应的等价传递函数矩阵和广义逆矩阵.根据文[15]可知,如果G(s)为行满秩矩阵,则它的广义逆为G+(s)=GT(-s)(G(s)GT(-s))-1.利用上述关系,可以求取被控对象的ETF模型.
令:
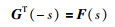
|
(2) |
通常可用1阶纯滞后模型(FOPDT)来近似描述实际系统,即:
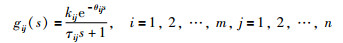
|
其中,kij为对象的稳态增益,τij为时间常数,θij为纯滞后时间.
对于Ĝ(s)矩阵中的各个元素,同样也可采用FOPDT模型:
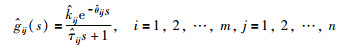
|
其中, 


针对上述FOPDT模型,根据式(1)有:
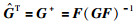
|
(3) |
令:
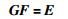
|
(4) |
则式(3)变为
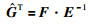
|
(5) |
即:

|
(6) |
其中|E|为E的行列式,adjEij为E的伴随矩阵.
在式(6)两边对s求1阶导数,有:
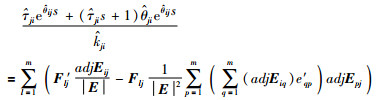
|
(7) |
其中eqp为矩阵E中的元素,e′qp为eqp的1阶导数.
继续在式(7)两边对s求1阶导数,有:
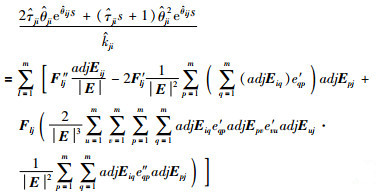
|
(8) |
其中eqp为eqp的2阶导数.令式(6)~(8)中的s=0,有:
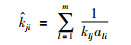
|
(9) |
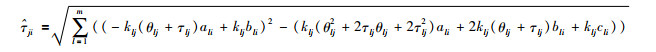
|
(10) |
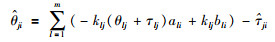
|
(11) |
其中,
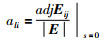
|
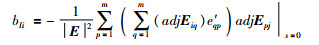
|
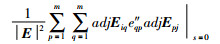
|
从式(9)~(11)可以看出,所求ETF模型的关键参数与被控过程参数之间存在直接解析关系,因此与文[13-14]的NERGA、NRNGA等ETF近似求法相比,具有更高的精度.同时,式(1)~(11)给出了ETF模型参数的通用解,不依赖于系统的维数,具有通用性,可适用于较高维数的多变量非方过程.
3 PI控制器设计由于等价传递函数已将来自不同回路的耦合考虑进去,因此针对已获得的等价传递函数可以利用求单输入单输出(SISO)的方法来设计相应的控制器.本文采用IMC-PID[16]的方法来设计控制器,因为该方法分析设计过程简单且具有很好的鲁棒性.
将已获得的ETF分解成两部分:
|
(12) |
其中pAi和pMj分别表示非最小相位部分和最小相位部分.期望的闭环传递函数为
|
(13) |
其中,λi是自主调节参数,mi是阶数,其选择的大小要满足控制器的正则性和可实现性.
根据期望的闭环传递函数可得控制器为
|
(14) |
其中qi是内模控制器,大小为
虽然上述控制可物理实现,但是并不是标准的PI形式,为了得到PI的形式,需要对上述控制器进行Maclaurin近似:
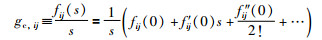
|
(15) |
其中,
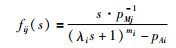
|
(16) |
将gc,ij写成标准的PI形式,即:
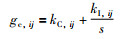
|
(17) |
其中kC,ij和kI,ij分别为控制的比例增益和积分增益.
联立式(15)和式(17)可得控制器的参数为

|
(18) |
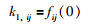
|
(19) |
当实际对象存在不确定时,会影响闭环系统控制性能,严重时会使系统变得不稳定.针对实际常见的乘性不确定分析所设计的控制器是否具有良好鲁棒稳定性.考虑输出不确定性ΔG0(s)=G(s)(I+Δ0(s)),其中Δ0(s)为乘性输出不确定性.根据文[17]可以得到确保闭环控制系统鲁棒稳定性的充分条件为
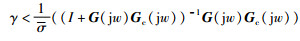
|
(20) |
其中γ代表鲁棒稳定程度,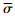
同时,为了比较多变量闭环系统的控制性能,利用控制系统的平方误差积分ISE(integral square error)性能指标[18]来进行比较.其计算公式为

|
(21) |
在式(21)中,表达式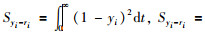
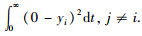
该指标(式(21))达到最小的系统就是某种意义下的最优控制系统.
4 仿真实例例1 以文[13]中2×3的非方系统为例,系统传递函数矩阵为
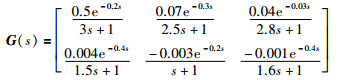
|
由文[11]可知,y1与u1和u3进行配对;y2与u2进行配对.根据过程传递函数矩阵,利用式(9)~(11)可以确定该过程回路的ETF模型分别为
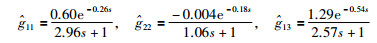
|
利用式(13)可得,期望的闭环传递函数分别为
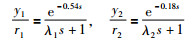
|
其中λi(i=1,2)为自主调节参数.通过调节λi使本文的γ值大于或等于文[13]和文[14]中的γ值,这里基于NERGA的ETF参数化方法[13]和基于NRNGA的ETF参数化方法[14]被用来进行仿真比较,由于NERGA方法采用幅值和相角裕度调节控制器参数,所以不存在λ1和λ2的值.根据式(18)和式(19)可得分散结构的PI控制器参数,如表 1所示.
| 方法 | 环路 | kC,ij j=1 |
kI,ij j=1 |
kC,ij j=2 |
kI,ij j=2 |
λ1 | λ2 | γ |
| 本文 | i=1 | 1.51 | 0.5 | 0 | 0 | 3 | 7 | 0.15 |
| i=2 | 0 | 0 | -36.98 | -35 | ||||
| i=3 | 0.26 | 0.10 | 0 | 0 | ||||
| ERGA | i=1 | 1.4 | 0.46 | 0 | 0 | - | - | 0.13 |
| i=2 | 0 | 0 | -37.93 | -37.93 | ||||
| i=3 | 0.18 | 0.06 | 0 | 0 | ||||
| RNGA | i=1 | 1.24 | 0.39 | 0 | 0 | 4 | 8 | 0.14 |
| i=2 | 0 | 0 | -34.15 | -30.41 | ||||
| i=3 | 0.16 | 0.09 | 0 | 0 |
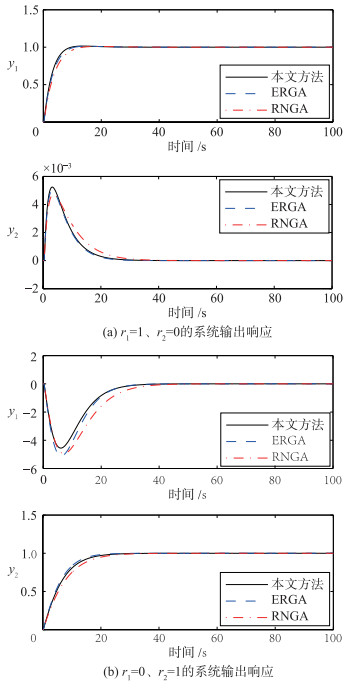
当参考输入r1=1,r2=0时,利用表 1中的控制器信息可以得到图 2(a)所示的系统输出响应;当参考输入r1=0、r2=1时,可以得到图 2(b)所示的系统输出响应.按照3种设计方法得到的系统ISE性能指标值见表 2.从图 2的闭环阶跃响应及表 2所示的ISE性能指标值可见,本文所提的ETF方法具有更好的控制性能.
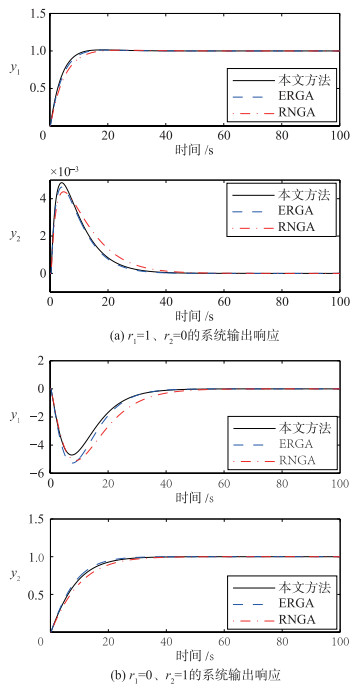
|
| 图 2 闭环阶跃响应 Figure 2 Closed-loop response to step changes |
| 方法 | 阶跃变化 | Sy1-ri值 | Sy2-ri值 | SISE |
| 本文 | r1 | 2.026 8 | 0.000 2 | 2.027 0 |
| r2 | 246.51 | 4.04 | 255.55 | |
| ERGA | r1 | 2.199 9 | 0.000 1 | 2.200 0 |
| r2 | 310.71 | 4.12 | 314.83 | |
| RNGA | r1 | 2.512 1 | 0.000 2 | 2.512 3 |
| r2 | 349.00 | 5.04 | 354.04 |
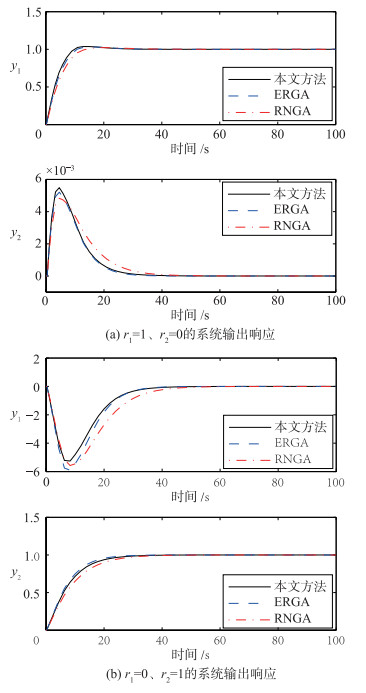
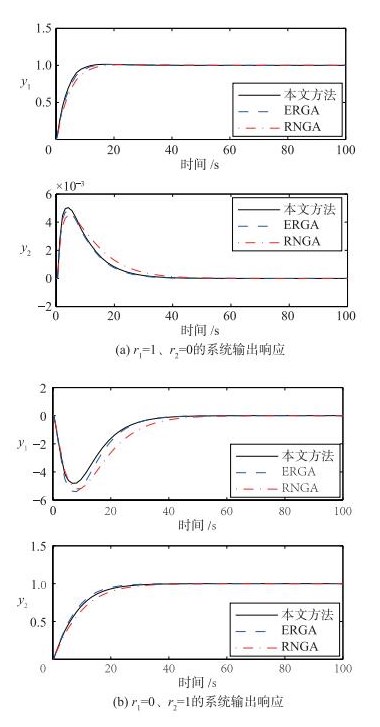
为了具体说明本文方法的鲁棒性,分别在被控过程的增益、时间常数和时滞增加30%的扰动.控制器参数不发生任何变化,当参考输入r1=1,r2=0时,对应的系统输出如图 3(a)~5(a)所示;当参考输入r1=0,r2=1时,对应的系统输出响应如图 3(b)~5(b)所示.当不同参数增加30%的扰动时,按照3种设计方法得到的系统ISE性能指标值见表 3.
| 方法 | 阶跃变化 | Sy1-ri值 | Sy2-ri值 | SISE |
| 增益发生+30%的变化量 | ||||
| 本文 | r1 | 1.599 9 | 0.000 2 | 1.600 1 |
| r2 | 184.66 | 3.428 1 | 188.09 | |
| ERGA | r1 | 1.730 4 | 0.000 2 | 1.730 6 |
| r2 | 232.37 | 3.2152 | 235.59 | |
| RNGA | r1 | 1.964 9 | 0.000 2 | 1.965 1 |
| r2 | 261.66 | 3.906 4 | 265.57 | |
| 时间常数发生+30%的变化量 | ||||
| 本文 | r1 | 2.637 7 | 0.000 2 | 2.637 9 |
| r2 | 283.15 | 5.168 5 | 288.32 | |
| ERGA | r1 | 2.834 5 | 0.000 2 | 2.834 7 |
| r2 | 356.36 | 4.878 0 | 361.24 | |
| RNGA | r1 | 3.179 2 | 0.000 2 | 3.179 4 |
| r2 | 389.11 | 5.822 7 | 394.93 | |
| 时滞发生+30%的变化量 | ||||
| 本文 | r1 | 2.382 3 | 0.000 2 | 2.382 5 |
| r2 | 261.90 | 4.929 2 | 266.83 | |
| ERGA | r1 | 2.565 6 | 0.000 2 | 2.565 8 |
| r2 | 330.08 | 4.637 0 | 334.72 | |
| RNGA | r1 | 2.893 5 | 0.000 2 | 2.893 7 |
| r2 | 367.14 | 5.582 3 | 372.72 | |
|
| 图 3 增益增加30%变化时的闭环阶跃响应 Figure 3 Closed-loop responses to step changes for+30% gain perturbation |
|
| 图 4 时间常数增加30%变化时的闭环阶跃响应 Figure 4 Closed-loop responses to step changes for +30% time constants perturbation |
|
| 图 5 时滞增加30%变化时的闭环阶跃响应 Figure 5 Closed-loop responses to step changes for +30% time delays perturbation |
从图 3~5和表 3可以看出,与文[13]和文[14]的方法相比,本文所提的方法具有更好的鲁棒性.
例2 在一些特殊情况下,HVAC(heating,ventilation,and air conditioning)[19]方形系统的第4个被控变量可以不作要求,此时方形的多变量系统可简化为如下非方系统:

|
首先利用非方相对增益阵列法[10]进行配对:y1与u1配对、y2与u2配对、y3与u3和u4配对;再求取该系统主回路的ETF模型:
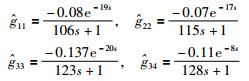
|
再根据式(13),期望闭环传递函数分别为
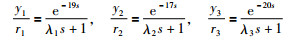
|
其中, λi(i=1,2,3)为自主调节参数,根据式(18)和式(19)可得分散结构PI控制器参数,如表 4所示.
| 方法 | 环路 | kC,ijj=1 | kI,ijj=1 | kC,ijj=2 | kI,ijj=2 | kC,ijj=3 | kI,ijj=3 | λ1 | λ2 | λ3 | γ |
| 本文 | i=1 | -17 | -0.16 | 0 | 0 | 0 | 0 | 50 | 60 | 60 | 0.97 |
| i=2 | 0 | 0 | -17 | -0.15 | 0 | 0 | |||||
| i=3 | 0 | 0 | 0 | 0 | -11 | -0.06 | |||||
| i=4 | 0 | 0 | 0 | 0 | -16 | -0.09 | |||||
| Davison | i=1 | -11.0 | -0.12 | 0 | 0 | 0 | 0 | - | - | - | 0.97 |
| i=2 | 0 | 0 | -11 | -0.13 | 0 | 0 | |||||
| i=3 | 0 | 0 | 0 | 0 | -8.32 | -0.09 | |||||
| i=4 | 0 | 0 | 0 | 0 | -2.34 | -0.03 |
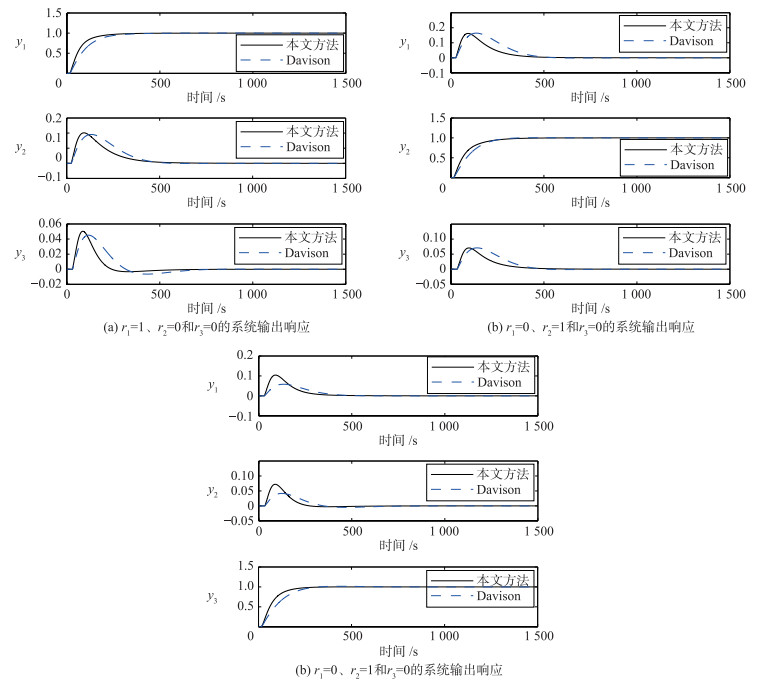
当采用Davison方法[20]设计控制器时,不涉及到λi值选取.当输入r1、r2、r3分别发生阶跃变化时,利用表 4中控制器参数,可得图 6所示的闭环系统输出响应.与之比较的是文[20]中的结果,按照两种设计方法得到的系统ISE性能指标值见表 5.从图 6和表 5可以看出,无论是针对一般非方系统或高维非方系统,本文所提的基于ETF的PI控制方法都可以得到满意的控制效果.
| 方法 | 阶跃变化 | Sy1-ri值 | Sy2-ri值 | Sy3-ri值 | SISE |
| 本文 | r1 | 46.12 | 4.89 | 0.18 | 51.19 |
| r2 | 2.91 | 50.63 | 0.52 | 54.06 | |
| r3 | 0.98 | 0.40 | 48.99 | 50.37 | |
| Davison | r1 | 61.66 | 6.06 | 0.25 | 67.97 |
| r2 | 4.53 | 64.44 | 0.81 | 69.78 | |
| r3 | 0.51 | 0.23 | 66.96 | 67.70 |
|
| 图 6 实例2的闭环阶跃响应 Figure 6 Closed-loop responses to step changes of example 2 |
本文利用等价传递函数与被控过程传递函数的广义逆之间的关系,推导出更高精度的ETF模型解析通式,并进一步设计分散结构的PI控制器.该方法不仅设计过程简单,具有精度高的优点且适用于高维的多变量非方系统.未来研究将该算法推广到含有扰动的多变量非方系统,将得到的ETF作为解耦器,并进一步设计控制器,实现很好的设定值跟踪性能和对扰动抑制作用.
| [1] | Liu J C, Chen N, Xia Y, et al. Modified internal model control for nonsquare systems based on Smith delay compensator control[J]. Sensors & Transducers , 2014, 165 (2) : 96–101. |
| [2] | Pop C I, De Keyser R, Ionescu C. A simplified control method for multivariable stable nonsquare systems with delays[C]//19th Mediterranean Conference on Control and Automation. Piscataway, NJ, USA:IEEE, 2011:382-387. |
| [3] | Liu J C, Chen N, Yu X. Modified two-degrees-of-freedom internal model control for non-square systems with multiple time delays[J]. Journal of Harbin Institute of Technology , 2014, 21 (2) : 122–128. |
| [4] | Rao A S, Chidambaram M. Decoupling Smith predictor for multivariable non-square systems with multiple time delays[J]. Journal of the Indian Institute of Science , 2013, 86 (3) : 235–256. |
| [5] | Chen J, He Z F, Qi X. A new control method for MIMO first order time delay non-square systems[J]. Journal of Process Control , 2011, 21 (4) : 538–546. DOI:10.1016/j.jprocont.2011.01.007 |
| [6] | Ren L H, Luo X L, Liu Y B, et al. A new variable pairing method and Its application in non-square multivariable systems[C]//10th World Congress on Intelligent Control and Automation(WCICA). Piscataway, NJ, USA:IEEE, 2012:2215-2220. |
| [7] | Luo Y H, Liu H B, Cai W J, et al. Control configuration selection based on RNGA for non-square multivariable processes[C]//Proceedings of 31st Chinese Control Conference. Piscataway, NJ, USA:IEEE, 2012:4722-4727. |
| [8] | Chen P L, Ou L L, Gu D Y, et al. Robust analytical scheme for linear non-square systems[C]//Proceedings of the 48th IEEE Conference on. Piscataway, NJ, USA:IEEE, 2009:1890-1895. |
| [9] | Sarma K L N, Chidambaram M. Centralized PI/PID controllers for nonsquare systems with RHP zeros[J]. Journal of the Indian Institute of Science , 2005, 85 (4) : 201–214. |
| [10] | Chang J W, Yu C C. The relative gain for non-square multivariable systems[J]. Chemical engineering science , 1990, 45 (5) : 1309–1323. DOI:10.1016/0009-2509(90)87123-A |
| [11] | Loh E J, Chiu M S. Robust decentralized control of non-square systems[J]. Chemical Engineering Communications , 1997, 158 (1) : 157–180. DOI:10.1080/00986449708936586 |
| [12] | Ammathil R, Narsaiah T B, Rao A S. Design of decentralized Smith predictor for multivariable non-square processes with multiple time delay[J]. International Journal of Modelling, Identification and Control , 2014, 21 (2) : 147–159. DOI:10.1504/IJMIC.2014.060008 |
| [13] | Chiranjeeevi T, Vijetha I V V, Chakravarthi B, et al. Tuning and control of multi-variable systems[J]. International Journal of electronics and electrical engineering , 2014, 2 (4) : 309–320. |
| [14] | Shen Y L, Sun Y X, Xu W. Centralized PI/PID controller design for multivariable processes[J]. Industrial & Engineering Chemistry Research , 2014, 53 (25) : 10439–10447. |
| [15] | Rao A S, Chidambaram M. Smith delay compensator for multivariable non-square systems with multiple time delays[J]. Computers and Chemical Engineering , 2006, 30 (8) : 1243–1255. DOI:10.1016/j.compchemeng.2006.02.017 |
| [16] | Lee Y, Park S, Lee M, Brosilow C. PID controller tuning for desired closed-loop responses for SI/SO systems[J]. AIChE Journal , 1998, 44 (1) : 106–115. DOI:10.1002/(ISSN)1547-5905 |
| [17] | Vu T N L, Lee M. Independent design of multi-loop PI/PID controllers for interacting multivariable processes[J]. Journal of Process Control , 2010, 20 (8) : 922–933. DOI:10.1016/j.jprocont.2010.06.012 |
| [18] | Jing Q B, Hao F, Wang Q. A multivariable IMC-PID method for non-square large time delay systems using NPSO algorithm[J]. Journal of Process Control , 2014, 23 (5) : 649–663. |
| [19] | Shen Y, Cai W J, Li S. Normalized decoupling control for high-dimensional MIMO processes for application in room temperature control HVAC systems[J]. Control Engineering Practice , 2010, 18 (6) : 652–694. DOI:10.1016/j.conengprac.2010.03.006 |
| [20] | Davison E J. Multivariable tuning regulators:The feed forward and robust control of a general servomechanism problem[J]. IEEE Transactions on Automatic Control , 1976, 21 (1) : 35–47. DOI:10.1109/TAC.1976.1101126 |



