1 引言
风能是世界上增长最快、最具竞争力的可再生能源[1].随着对风能需求的增加,风电场数量不断上升.然而受地理环境条件限制,风电场多建在沙漠、海上等资源丰富但环境恶劣的地区[2],风力机易发生故障且得不到及时维修,对风力发电机组的安全运行造成严重威胁,影响风电系统稳定性甚至导致系统停机.现代风力机多采用容错控制方法维持并保证系统的稳定运行,而故障诊断则是其前提和必要条件[3].
桨距系统是风力机的重要组成部分.当风速高于额定风速且低于切出风速时,风力机桨距系统通过改变桨距角的大小来调整所捕获风能的功率,从而保证风电机组输出功率的恒定[4].然而据统计,在完整的一年中(2012年),桨距系统为故障数量最多的部分[5].桨距角的大小由桨距系统中桨距执行器通过旋转叶片控制[6],桨距执行器常见油液空气含量高、液压泄漏和泵磨损故障[7].当桨距系统发生此类故障后,其动态响应速度受到限制,将会造成风电机组输出功率不稳定.而且,桨距系统总是伴随着风机叶片的旋转而工作,若桨距系统出现故障,很有可能造成叶片断裂甚至风力机倒塌等风电机组严重事故[8].因此,及时准确诊断出风力机桨距系统故障,对于风力发电机组稳定安全运行至关重要.
近年来,针对风力机桨距系统的故障诊断研究受到国内外学者的关注,桨距系统的故障诊断方法也得到了更进一步的发展.文[9-10]针对风力机叶根传感器和桨距执行器故障,基于风机系统的动态模型,分别设计观测器和滤波器产生冗余信息进行故障检测和估计.文[11]基于桨距系统动态模型,采用自适应参数估计算法检测桨距系统液压泄漏故障.文[12]则利用模糊建模以及辨识方法构造基于模型的故障检测和诊断结构,实现桨距传感器的故障诊断.文[13]采用区间观测器对风电系统中传感器故障和执行器故障进行诊断.文[14]基于风力机桨距系统的辨识模型,提出采用基于多新息随机梯度算法对桨距执行器故障进行诊断.文[15]建立风力发电机组桨距系统键合图模型,提出采用基于键合图模型的方法对桨距系统故障进行诊断,并且通过因果理论建立故障树以分析故障源.文[16]中提出一种基于机器学习的图解模型方法,利用高斯非循环图解模型和套索估计对风力机桨距系统故障进行诊断.文[17]中通过建立风力发电机组桨距系统动态模型,采用基于风电机组物理特性的数学模型的方法对桨距系统进行故障检测.文[18]利用风力发电机组监测到的正常状态下的数据和故障状态下的信息,分别建立桨距系统正常和故障时刻的数据样本集,基于Relief方法对风电机组桨距系统的故障特征参数进行挖掘.
本文采用基于观测器的多新息随机梯度辨识算法(Observer-based Multi-Innovation Stochastic Gradient algorithm,O-MISG),对风力机桨距系统故障进行诊断.系统辨识通过系统的输入输出数据能够估计系统参数[19].桨距系统故障时,其系统状态以及系统参数均发生相应改变,桨距系统状态空间模型则包含了未知状态和未知参数且二者为非线性乘积关系,使得辨识问题变得复杂.根据桨距系统的观测器规范型状态空间系统模型得到系统的辨识模型,采用多新息随机梯度辨识算法,结合观测器方法实现系统状态和参数的交互估计[20].最终,根据参数的变化及其变化的大小,检测系统故障的发生并识别故障类型.
2 风力机及其桨距系统故障描述风力机通过叶片的转动,将捕捉的风能转化为机械功率.而后通过传动系统将获得的气动转矩传递到发电机以发出电能.风力发电系统包含气动系统、桨距系统、传动系统和功率系统[21].其各个系统间的相互连接关系如图 1所示.其中,βref(t)为桨距角参考值,β(t)为桨距角,vr(t)为风速,Ta(t)为气动转矩,ωr(t)为转子速度,ωg(t)为发电机转速,Tg(t)为发电机转矩,Pg(t)为发电机产生的电能.

|
| 图 1 风力发电系统的子系统间相互连接关系 Figure 1 Interconnection diagram among subsystems of the wind turbine system model |
气动系统风力机通过叶片将风能转换到转子侧,转子捕获的风能依赖风速、空气密度、桨叶扫过的有效面积及功率系数.功率系数取决于叶尖速比和桨距角,叶尖速比是叶片尖端的圆周速度与风速的比值,表示叶轮在风速变化时的运行状态.转子处的气动转矩则为转子捕获的风能与转子速度之比,该气动转矩随后传递入传动系统.
传动系统主要包括风轮转子、低速轴、齿轮箱和高速轴.风轮捕获风中的动能,使低速轴转动,从而产生相应的机械转矩,然后由齿轮箱连接高速轴,实现低速向高速的变换,将机械转矩传递到高速轴,最后由高速轴连接入发电机.
功率系统包含发电机和变流器,电能由发电机产生,通过变流器接入电网中.发电机转矩受参考转矩控制,经变流器输出至发电机.
风力机桨距系统由3个完全一致的桨距执行器组成,桨距执行器通过旋转叶片以控制桨距角的大小.桨距执行器可以建模为桨距角β(t)和桨距角参考值βref(t)之间的传递函数. β(t)是桨距系统的输出,βref(t)是风力机控制器给出的设定值.桨距执行器的二阶传递函数模型如下[21]:
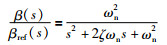
|
(1) |
式中,ωn为桨距执行器自然频率,ζ为桨距执行器阻尼系数.
桨距执行器输出的动态描述为
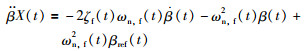
|
(2) |
式中,f表示3种情况,分别为油液空气含量高、液压泄漏和泵磨损,即f=ha,h1,pw.
故障通过改变桨距执行器自然频率和阻尼系数的值使得桨距系统的动态特性变差.故障作用下,桨距执行器自然频率和阻尼系数从标称值ωn,0和ζ0改变为3种故障所对应的参数值ωn,ha和ζha,ωn,hl和ζhl,以及ωn,pw和ζpw.桨距执行器故障时自然频率ωn,f(t)和阻尼系数ζf(t)的参数值如表 1[21]所示.
| 故障类型 | 参数值 |
| 无故障 | ωn,0=11.11 rad/s,ζ0=0.6 |
| 油液空气含量高 | ωn,ha=5.73 rad/s,ζha=0.45 |
| 液压泄漏 | ωn,hl=3.42 rad/s,ζhl=0.9 |
| 泵磨损 | ωn,pw=7.27 rad/s,ζpw=0.75 |
参数ωn,f(t)和ζf(t)的表达式分别为

|
(3) |
式中,ηf(t)即ηha(t)、ηhl(t)和ηpw(t)分别为油液空气含量高、液压泄漏和泵磨损故障的指示信号且0≤ηf(t)≤1.显然,当指示信号为0时表示桨距系统无故障发生,然而当指示信号为1时表示故障发生.油液空气含量高是可以消失的潜在故障,ηha(t)=1相当于油液中空气含量为15%,若故障发生,此时参数值ωn,ha=5.73 rad/s和ζha=0.45.液压泄漏也是一个潜在故障,但是不对系统进行维修该故障无法消除. ηhl(t)=1所对应的为液压泄漏导致压力值降低到正常水平的50%,若故障发生,此时参数值ωn,hl=3.42 rad/s和ζhl=0.9.泵磨损是无法逆转的故障,只能对泵进行更换. ηpw(t)=1对应的故障相当于泵输出压力下降到约为75%的压力级,故障发生,此时参数值ωn,pw=7.27 rad/s和ζpw=0.75.
3 故障诊断方法对于风力机桨距系统,基于系统辨识算法的故障诊断方法需要系统输入数据桨距角参考值βref(t)和输出数据桨距角β(t),从而实现对系统参数的辨识.桨距角的数据采集主要由桨距角传感器完成,若桨距角传感器发生故障或者其它异常,导致所采集数据出现误差,则会影响参数的辨识结果,造成故障源的误诊断.为了避免类似误诊断,提出O-MISG辨识算法,通过观测器对桨距系统进行状态估计,将桨距系统状态的估计值代替其测量值进行参数辨识,实现桨距系统的状态和参数联合估计,以此完成故障的准确诊断.
3.1 桨距系统辨识模型对于如式(2)所示的桨距执行器动态描述,选择状态量[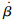
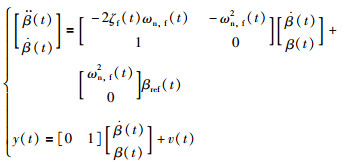
|
(4) |
取采样周期为T0,对式(4)进行离散化可得:
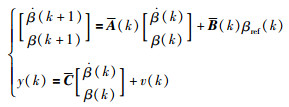
|
(5) |
式中,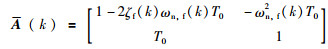
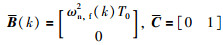
系统的能观测性矩阵为
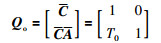
|
rank Qo=2,能观测性矩阵满秩,故系统能观测.
令
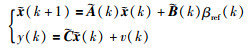
|
(6) |
式中,
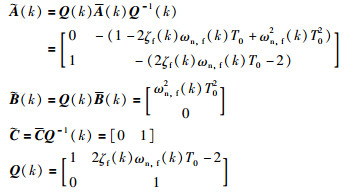
|
于是,定义新的系统状态向量x(k)=[x1(k),x2(k)]T,x1(k)=β(k),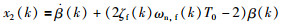
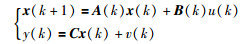
|
(7) |
式中,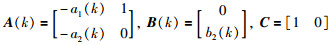
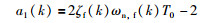
|
(8) |
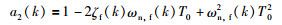
|
(9) |
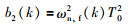
|
(10) |
根据式(7)可得:
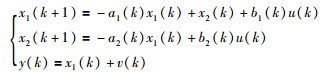
|
(11) |
根据文[20]中所述方法,有:
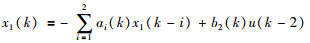
|
(12) |
定义参数向量θ(k)和信息向量φ(k):

|
所以,桨距系统的辨识模型为
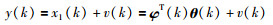
|
(13) |
桨距系统故障时,自然频率和阻尼系数发生改变,由式(8)~(10)可知,参数a1、a2和b2发生相应改变.所以,根据式(13)所示桨距系统的辨识模型,通过O-MISG辨识算法能够辨识出参数a1、a2和b2的大小,根据其发生的变化及其变化量的值判断桨距系统故障的发生和类型.
3.2 基于观测器的多新息随机梯度辨识算法基于式(13)所述的系统辨识模型,随机梯度辨识算法为
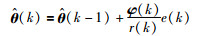
|
(14) |
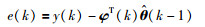
|
(15) |
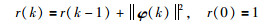
|
(16) |
式中,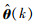
设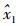
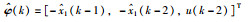
|
定义堆积输出向量Y(p,k)和信息矩阵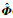
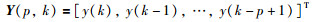
|
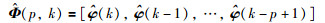
|
随机梯度辨识算法中,式(14)中e(k)为标量新息,引入新息长度p将e(k)扩展成为新息向量E(p,k)为
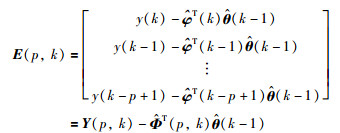
|
由于状态量未知,所以利用观测器估计的状态量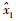
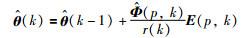
|
(17) |
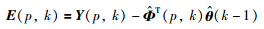
|
(18) |
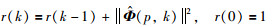
|
(19) |
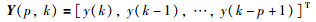
|
(20) |
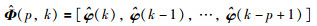
|
(21) |
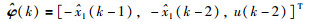
|
(22) |
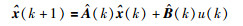
|
(23) |

|
(24) |
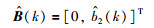
|
(25) |
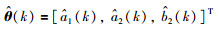
|
(26) |
本文根据4.8 MW级风力发电系统实际参数,基于文中所述风力机基准模型以及所提出的故障诊断方法,对风力机桨距系统故障的诊断进行仿真.
根据式(3)可知,文中所研究的油液空气含量高、液压泄漏和泵磨损三种桨距系统故障下,参数ωn,f(t)和ζf(t)的表达式具有相同结构,故文中选择油液空气含量高这一故障进行仿真,以验证所提出故障诊断方法的可行性和有效性.当发生油液空气含量高故障时,自然频率ωn从正常值11.11 rad/s降低变为5.73 rad/s,阻尼系数ζ从正常值0.6变为0.45,导致桨距系统的动态特性变差.参数a1,a2和b2根据自然频率和阻尼系数的变化相应改变,采样周期为T0=0.01 s.无故障和油液空气含量高故障下参数a1,a2和b2的值如表 2所示.
| 参数 | 无故障时参数值 | 故障时参数值 |
| a1 | -1.866 68 | -1.948 43 |
| a2 | 0.879 023 21 | 0.951 713 29 |
| b2 | 0.012 343 21 | 0.003 283 29 |
仿真中,将故障的出现设置在100 s~200 s,故障指示信号为
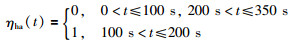
|
根据仿真设置,风力机在0 s~100 s无故障运行,自然频率和阻尼系数为正常量11.11 rad/s和0.6,参数a1、a2和b2均为理论正常值,分别为-1.866 68,0.879 023 21和0.012 343 21.在100 s~200 s期间,当油液空气含量高故障发生时,自然频率和阻尼系数变化为故障值5.73 rad/s和0.45,故参数a1、a2和b2均相应变为故障时刻值-1.948 43,0.951 713 29和0.003 283 29. 200 s之后故障消失,参数值均恢复至正常值.
文中同时采用O-MISG辨识算法和最小二乘(least squares,LS)算法对油液空气含量高故障进行仿真诊断,仿真结果如图 2~4.
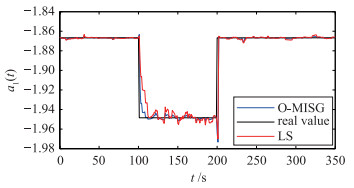
|
| 图 2 参数a1的值 Figure 2 Parameter value of a1 |
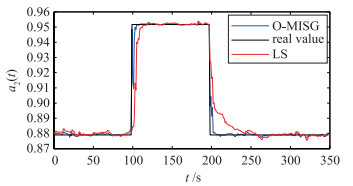
|
| 图 3 参数a2的值 Figure 3 Parameter value of a2 |
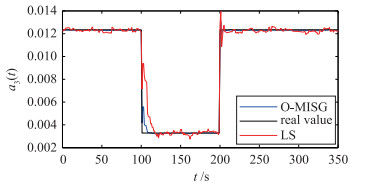
|
| 图 4 参数b2的值 Figure 4 Parameter value of b2 |
由仿真结果图可知,相较于LS算法,O-MISG算法的收敛速度更快,辨识精度更高,能够更好地跟踪参数值的变化,更好地估计出变化的参数量,并最终根据参数的变化及其变化的大小和方向确定故障的发生和类型,实现桨距系统不同类型的故障诊断.同时,由于采用O-MISG辨识算法进行参数辨识过程中的数据为系统状态的估计值,避免了状态测量值误差可能带来的辨识误差影响,减少了故障的误诊断现象.
5 结论风力机桨距系统故障会使得桨距系统动态特性变慢,从而导致风力发电机组输出功率不稳定.根据桨距系统故障会引起系统参数产生变化的特点,本文利用系统辨识方法对风力机桨距系统故障进行诊断,将故障诊断问题转化为系统参数辨识问题.基于风力机桨距执行器的观测器规范型状态空间系统模型,采用O-MISG辨识算法实现系统状态和参数的交互估计,参数辨识所需的状态测量值由观测器得到系统的状态估计值代替,从而防止因传感器故障等原因引起的桨距系统状态测量误差对系统参数辨识产生影响,以得到系统参数的准确辨识结果.最终依据所辨识参数的变化实现对桨距执行器故障的诊断.仿真结果验证了该辨识算法对风力机桨距系统故障诊断的可行性和有效性.
| [1] | Feng Y, Lin H Y, Ho S L, et al. Overview of wind power generation in China:status and development[J]. Renewable and Sustainable Energy Reviews , 2015, 50 : 847–858. DOI:10.1016/j.rser.2015.05.005 |
| [2] | Perveen R, Kishor N, Mohanty S R. Off-shore wind farm development:Present status and challenges[J]. Renewable and Sustainable Energy Reviews , 2014, 29 : 780–792. DOI:10.1016/j.rser.2013.08.108 |
| [3] | Kamal E, Aitouche A, Ghorbani R, et al. Fuzzy scheduler fault-tolerant control for wind energy conversion systems[J]. IEEE Transactions on Control Systems Technology , 2014, 22 (1) : 119–131. DOI:10.1109/TCST.2013.2246162 |
| [4] | Watson S J, Xiang B J, Yang W, et al. Condition monitoring of the power output of wind turbine generators using wavelets[J]. IEEE Transactions on Energy Conversion , 2010, 25 (3) : 715–721. DOI:10.1109/TEC.2010.2040083 |
| [5] | 张镇, 关书强. 风电机组故障统计分析研究[J]. 风能 , 2013 (8) : 68–71. Zhang Z, Guan S Q. An analysis of wind turbine fault statistics[J]. Wind Energy , 2013 (8) : 68–71. |
| [6] | 秦斌, 王欣, 郭百顺, 等. 基于支持向量机权系数的独立变桨学习控制[J]. 信息与控制 , 2015, 44 (6) : 685–689, 696. Qin B, Wang X, Guo B S, et al. Individual pitch learning control based on support vector weight coefficient[J]. Information and Control , 2015, 44 (6) : 685–689, 696. |
| [7] | 宋锦, 吴定会, 李意扬, 等. 基于虚拟传感器的风力机LPV容错控制[J]. 信息与控制 , 2015, 44 (6) : 685–689, 486. Song J, Wu D H, Li Y Y, et al. LPV fault tolerant control of wind turbines based on virtual sensor[J]. Information and Control , 2015, 44 (6) : 685–689, 486. |
| [8] | 李辉, 杨超, 李学伟, 等. 风机电动变桨系统状态特征参量挖掘及异常识别[J]. 中国电机工程学报 , 2014, 34 (12) : 1922–1930. Li H, Yang C, Li X W, et al. Conditions characteristic parameters mining and outlier identification for electric pitch system of wind turbine[J]. Proceedings of the CSEE , 2014, 34 (12) : 1922–1930. |
| [9] | Wei X, Verhaegen M, Van Engelen T. Sensor fault detection and isolation for wind turbines based on subspace identification and Kalman filter techniques[J]. International Journal of Adaptive Control and Signal Processing , 2010, 24 (8) : 687–707. |
| [10] | Wei X, Verhaegen M. Sensor and actuator fault diagnosis for wind turbine systems by using robust observer and filter[J]. Wind Energy , 2011, 14 (4) : 491–516. DOI:10.1002/we.v14.4 |
| [11] | Wu X, Li Y, Li F, et al. Adaptive estimation-based leakage detection for a wind turbine hydraulic pitching system[J]. IEEE/ASME Transactions on Mechatronics , 2012, 17 (5) : 907–914. DOI:10.1109/TMECH.2011.2142400 |
| [12] | Badihi H, Zhang Y, Hong H. Fuzzy gain-scheduled active fault-tolerant control of a wind turbine[J]. Journal of the Franklin Institute , 2014, 351 (7) : 3677–3706. DOI:10.1016/j.jfranklin.2013.05.007 |
| [13] | Blesa J, Rotondo D, Puig V, et al. FDI and FTC of wind turbines using the interval observer approach and virtual actuators/sensors[J]. Control Engineering Practice , 2014, 24 (3) : 138–155. |
| [14] | Wu D, Li Y. Fault diagnosis of variable pitch for wind turbines based on the multi-innovation forgetting gradient identification algorithm[J]. Nonlinear Dynamics , 2015, 79 (3) : 2069–2077. DOI:10.1007/s11071-014-1795-1 |
| [15] | Yang X Y, Liu W, Li J X. Fault diagnosis based on bond graph for hydraulic variable pitch system[J]. Applied Mechanics & Materials , 2011, 48/49 : 1401–1405. |
| [16] | Aloraini A, Sayed-Mouchaweh M. Graphical model based approach for fault diagnosis of wind turbines[C]//201413th International Conference on Machine Learning and Applications(ICMLA). Piscataway, NJ, USA:IEEE, 2014:614-619. |
| [17] | 赵洪山, 连莎莎, 邵玲. 基于模型的风电机组变桨距系统故障检测[J]. 电网技术 , 2015, 39 (2) : 440–444. Zhao H S, Lian S S, Shao L. A model-based fault detection for variable-pitch system of wind turbines[J]. Power System Technology , 2015, 39 (2) : 440–444. |
| [18] | 李学伟.基于数据挖掘的风电机组状态预测及变桨系统异常识别[D].重庆:重庆大学, 2012. Li X W.Data-based condition prediction of wind turbine generator system and outlier identification of pitch system[D].Chongqing:Chongqing University, 2012. |
| [19] | 丁锋. 系统辨识新论[M]. 北京: 科学出版社 ,2013 . Ding F. System identification-new theory and methods[M]. Beijing: Science Press , 2013 . |
| [20] | 丁峰, 马兴云. 规范状态空间系统辨识方法[J]. 南京信息工程大学学报:自然科学版 , 2014, 6 (6) : 481–504. Ding F, Ma X Y. Identification methods for canonical state space systems[J]. Journal of Nanjing University of Information Science and Technology:Nature Science Edition , 2014, 6 (6) : 481–504. |
| [21] | Esbensen T, Sloth C. Fault diagnosis and fault-tolerant control of wind turbines[M]. Aalborg: Aalborg University , 2009 . |
| [22] | Ding F. Combined state and least squares parameter estimation algorithms for dynamic systems[J]. Applied Mathematical Modeling , 2014, 38 (1) : 403–412. DOI:10.1016/j.apm.2013.06.007 |
| [23] | Ma X Y, Ding F. Gradient-based parameter identification algorithms for observer canonical state space systems using state estimates[J]. Circuits, Systems, and Signal Processing , 2015, 34 (5) : 1697–1709. DOI:10.1007/s00034-014-9911-5 |



