1 引言
自然界中的个体和人造工程在功能及结构上都存在差异,其系统描述是混合多种动力学方程的复杂系统,因此最近一些学者着力于研究由一阶和二阶智能体组成的异质多智能体系统. Zheng等[1-2]分别在二阶智能体的速度信息可测和不可测的情形下,给出当信息流图具有固定无向拓扑结构时,异质多智能体系统在线性一致性算法和饱和一致性算法下的一致性条件.在此基础上,冯元珍[3]将文[1]中的相关结论推广到有向拓扑结构情形.宋运忠[4]运用图论、圆盘定理和李亚普诺夫理论,证明了异质多智能体系统在动态切换的无向拓扑下能够达到拟平均一致. Liu等[5]利用非负矩阵理论得到了具有有界通信时延的异质多智能体系统在切换连接拓扑下的一致性条件.在文[5]基础上,梁有明[6]通过构造李亚普洛夫函数,利用线性矩阵不等式得到了具有时变输入时延的异质多智能体系统的一致性条件. Dai[7]进一步利用李亚普诺夫方法研究了具有静态领航者的时延异质多智能体系统一致性.然而,迄今为止异质多智能体的分组一致性鲜有研究.
当多智能体系统受到环境、状态、时间改变的影响,或是多个智能体分布协调完成多个不同任务时,多智能体系统中都会出现多个不同一致状态的现象[8],由此激发关于多智能体系统组一致性问题的研究.在组一致性问题中,可以将被研究的多智能体系统看作是由多个多智能体子系统组成的系统,信息交流不仅存在于同一个子系统内部的智能体之间,而且存在于不同子系统的智能体之间.异质多智能体系统的组一致意味着不同子系统中智能体的动力学不尽相同,每个子系统分别实现一致性,而彼此之间的一致状态没有必然联系.
Yu等[8]最早提出了多智能体系统组一致性的概念,并在无向连通拓扑结构下,实现了一阶系统的两分组及多分组一致性.在此基础上,Feng等[9]研究了二阶多智能体系统的组一致性问题,并给出组一致状态的表达式.然而,上述相关研究工作都是基于入度平衡的假设条件开展的,要求一个组中每一个节点到其它组中所有节点的邻接权重之和等于0,即两个子网间的相互影响为零. Tan[10]在此基础上,放宽了前提条件,要求同一组中每一个节点到其它组中所有节点的邻接权重之和在任意时刻保持同一常量.在实际系统中,智能体间的彼此通信不可能恰好满足上述两种特殊的条件.
本文针对一类一阶、二阶异质多智能体系统的组一致性问题,提出了一种无假设条件的异质多智能体系统静态组一致性算法,运用矩阵理论、稳定性理论和线性矩阵不等式,分别在无时延和多时延的情况下,得到了异质多智能体系统实现组一致性的充分条件,并给出通信时延上界和输入时延上界的线性矩阵不等式表示.
2 问题描述 2.1 多智能体系统的拓扑描述在智能体组成的多智能体系统中,智能体之间通过信息流的作用相互耦合,构成了连接拓扑结构.若将智能体看作有向图的节点,信息流的流向看作有向图的有向边,则多智能体系统的信息交换拓扑可以用图论的知识进行描述:假设多智能体系统为一个具有n(n≥2)个节点的权重有向图G=(V,E,A),由节点集V={v1,…,vn},边集E⊆V×V及权重邻接矩阵A=[aij]∈Rn×n组成,节点的下标属于一个有限集I={1,2,…,n}.当且仅当aij>0,有向图中的边(vi,vj)存在,并假定aii=0,i∈I.节点的邻接集用Ni表示,Ni={vj∈V:(vi,vj)∈E}.定义节点vi的输入度为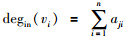
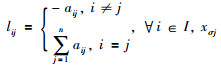
在有向图G中,如果从节点vi到节点vj之间有一条路径,那么节点vj称为从节点vi可达,即智能体i能够接收到智能体j发出的信息;否则为不可达.如果一个节点从有向图中任意其它节点都是可达的,那么称该节点是全局可达.
2.2 异质多智能体系统模型假设异质多智能体系统由n1个二阶智能体和n2=n-n1个一阶智能体组成.
第i个二阶智能体的动力学方程为
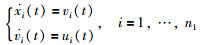
|
(1) |
其中xi(t)、vi和ui分别表示第i个二阶智能体的位置、速度和控制输入[3].
第i个一阶智能体的动力学方程为
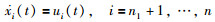
|
(2) |
其中xi(t)和ui分别表示第i个一阶智能体的位置及控制输入.
为后面进一步的论述,首先给出子图的定义.
定义1[11] 有向图G1=(V1,E1,A1)被称为有向图G=(V,E,A)的子图,当且仅当V1⊆V,E1⊆E,邻接矩阵A1的元素属于邻接矩阵A.
不失一般性,假设异质多智能体系统拓扑图G=(V,E,A)包含n个节点,其中子图G1包含前n1个二阶智能体节点,子图G2包含后n2个一阶智能体节点.子图的节点集合分别为V1={v1,…,vn1},V2={vn1+1,…,vn},节点的下标集I1={1,2,…,n1},I2={n1+1,…,n}.由定义1知,V=V1∪V2,I=I1∪I2.
2.3 组一致性算法在设计一致性算法前,首先定义异质多智能体系统的静态组一致性:
定义2 对于给定的初始条件(xi(0),vi(0)),i∈I1和xi(0),i∈I2,当满足:
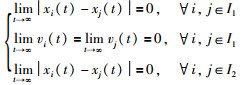
|
(3) |
称异质多智能体系统实现静态组一致.此外,若异质多智能体系统的平衡点满足:
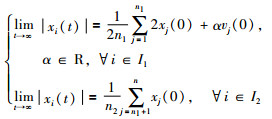
|
(4) |
则称异质多智能体系统实现静态组平均一致.此处定义了包含两个组的异质多智能体系统的组一致性,对于多组的情况,可用类似的方法进行定义.
针对无领航者的异构多智能体系统,本文提出带多通信时延[12]的组一致性算法(5):
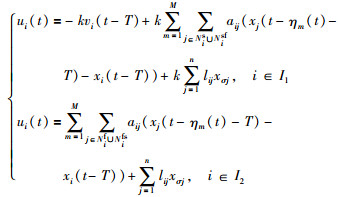
|
(5) |
异质多智能体系统式(1)和式(2)的连接拓扑用有向图G=(V,E,A)表示,其中aij>0为邻接矩阵A的元素,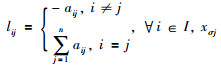
虽然在实际的系统中,通信时延和输入时延均可能时变,但考虑到通信时延常随着智能体之间的连接拓扑结构、所处环境等因素变化,而输入时延存在于控制器与执行器之间,其变化较通信时延要缓慢得多,故本文假设输入时延定常.
令ei(t-τ(t))=xi(t-τ(t))-xσi,∀i∈I,将算法(5)代入式(1)和式(2),得到多时延异质多智能体系统的闭环形式:
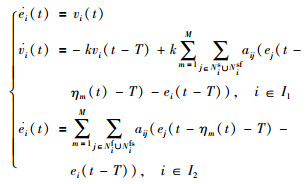
|
(6) |
进一步做模型变换[13],假设速度vi是关于控制增益k和位置信息xi的变量vi(t)=vi(t)/k+xi(t),∀i∈I1,vi(t)=k(i(t)-xi(t)),vi(t)-0=k((vi(t)-xσi)-(xi(t)-xσi)),令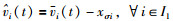

|
则在一致性算法(5)作用下,二阶智能体系统式(1)和一阶智能体系统式(2)的统一闭环方程描述:
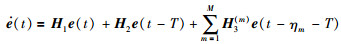
|
(7) |
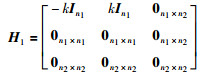
|
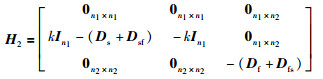
|
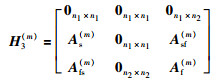
|
其中,In1是n1阶单位阵.定义:
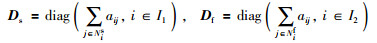
|
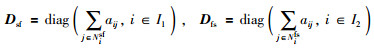
|
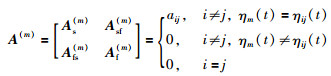
|
引理1[14] 若n阶有向图G具有全局可达节点,则其拉普拉斯矩阵L满足rank(L)=n-1,等价于L有且仅有一个零特征值,其余n-1个特征值均具有正实部.
引理2[15] 对于任意实可微向量函数x(t)∈Rn,常数矩阵W=WT>0∈Rn×n及0≤τk(t)≤hk,以下不等式成立:
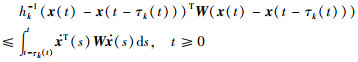
|
假设系统不存在任何时延,则算法(5)简化为
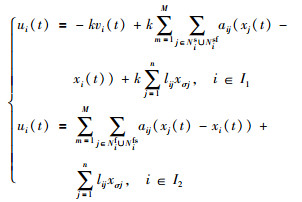
|
(8) |
闭环式(7)化为
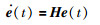
|
(9) |
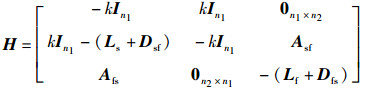
|
其中,Ls和Lf分别为n1个二阶智能体构成的连接拓扑的拉普拉斯矩阵与n2个一阶自主体智能体构成的连接拓扑的拉普拉斯矩阵,Asf∈Rn1×n2和Afs∈Rn2×n1为一阶智能体与二阶智能体之间的邻接矩阵,G的拉普拉斯矩阵L=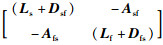
定理1 若控制增益k≥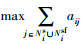
证明 根据Gershgorin圆盘定理,矩阵H的特征值λl满足λ∈∪Gl,l=1,2,…,n.
1)当l=1,…,n1时:
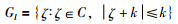
|
2)当l=n1+1,…,2n1,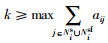
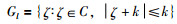
|
3)当l=2n1+1,…,n1+n时:
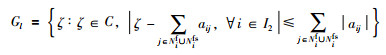
|
其中,C是复平面,容易得到矩阵H的特征值λ分布在复平面的原点以及负半平面上,因此矩阵H是半负定矩阵.
对H进行初等行列变换,其秩不变,即rank(H)=rank(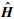
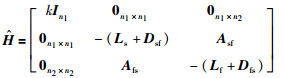
|
得到rank(H)=rank(L)+n1,由系统拓扑图G具有全局可达节点知,rank(H)=rank(L)+n1=n-1+n1.因此矩阵H有且只有一个零特征值.同时,定义系统的李亚普诺夫函数为
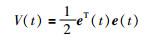
|
(10) |
结合式(9),得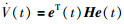
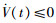
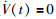
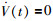
推论1 当满足定理1且系统拓扑图G是具有全局可达节点的平衡图,算法(8)能够实现异质多智能体系统式(1)和(2)的静态组平均一致.
证明 因为矩阵-H有单一零特征值且其它特征值均具有正实部,根据引理1,等价于矩阵-H对应的n阶有向图具有全局可达节点.系统拓扑图G是平衡图,易验证矩阵-H的列和为0,加之矩阵-H对应的n+n1阶有向图具有全局可达节点,因此误差系统(9)可以实现平均一致.根据定理1,误差系统(9)的稳态解是0n+n1,系统式(1)和式(2)的稳态平衡点一般形式[xs*T,vs*T,xf*T]=[(α12n1)T,(β1n2)T],于是得到2n1α+n2β=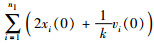
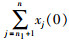
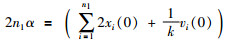
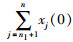
本节针对固定拓扑下的时变多时延异质多智能体系统,利用李亚普诺夫方法得到使系统实现渐近组一致的充分条件,并给出通信时延上界dm和输入时延T的线性矩阵不等式表示.这里假设t≥0,通信时延ηm(t)满足条件:
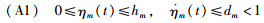
|
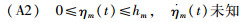
|
定理2 考虑固定拓扑有向图G,图G全局可达且满足时延条件(A1).如果存在对称正定矩阵P,Q1, Q2,R1,R2∈Rn×n,使得线性矩阵不等式(11)成立,那么对于ηm(t)≤hm的系统,所有智能体能实现渐近分组一致.
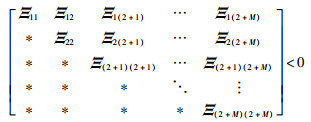
|
(11) |
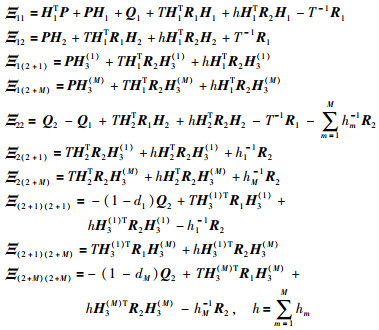
|
证明 定义式(7)所描述系统的Lyapunov-Krasovskii函数如下:
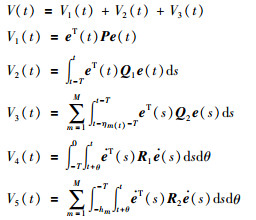
|
沿着系统的解轨迹求导:
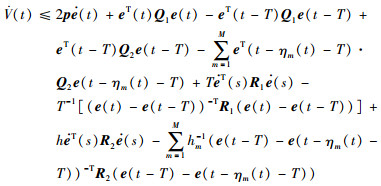
|
由式(7)和引理2,得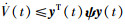
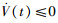
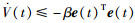
推论1 考虑固定拓扑有向图G,图G全局可达且满足时延条件(A2).如果存在对称正定矩阵P,R1,R2∈Rn×n,使得线性矩阵不等式(12)成立,那么对于ηm(t)≤hm,所有智能体渐近地实现渐近分组一致.

|
(12) |
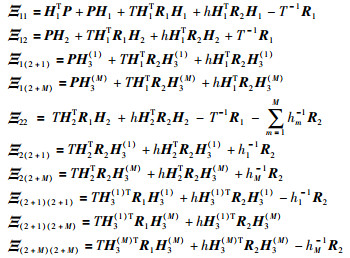
|
证明 定义式(7)所描述系统的Lyapunov-Krasovskii函数:
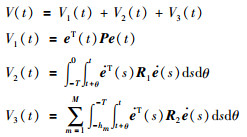
|
余下证明过程与定理2类似.
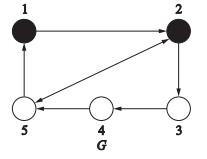
4 仿真实例考虑5个智能体组成的多智能体系统,如图 1所示,其中1、2是二阶智能体,3、4、5是一阶智能体. 5个智能体互连构成连通拓扑图G,相应的邻接矩阵限于0-1矩阵.
|
| 图 1 系统拓扑结构 Figure 1 System topology structure |
假定各智能体的初始状态ζT(0)=[xsT(0),vT(0),xfT(0)]=[1, 2, 2, 4, 0, 2, 1],图G是具有全局可达点的平衡图,预计稳态平衡点xσ1=xσ2=2.25,xσ3=xσ4=xσ5=1.
(1)假定各智能体间不存在时延,根据推论1,得到当控制增益k≥2时,异质多智能体系统实现静态组平均一致.
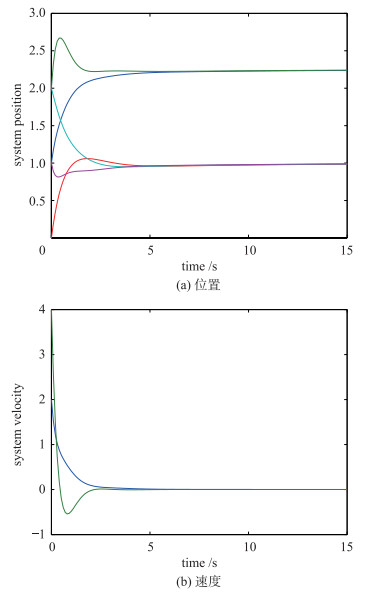
取k=2,异质多智能体系统中智能体的状态轨迹如图 2所示,可以看出二阶智能体组的位置收敛至2.25,速度收敛至0,一阶智能体组的位置收敛至1,符合推论1的结论.
|
| 图 2 无时延系统状态轨迹 Figure 2 The state trajectory of system without delay |
(2)假定固定拓扑图G中,边(1,2),(2,3),(3,4),(4,5)具有通信时延η1(t),边(2,5),(5,2)具有通信时延η2(t),同时智能体存在输入时延T.取控制增益k=2,d1=d2=0.根据定理2,调用LMI(linear matrix inequation)工具箱求解式(11),得到当输入时延T≤0.44时,通信时延上界h1、h2在0.1~10 000之间取值都不会影响线性矩阵不等式的可行性.一定程度上可以认为通信时延与系统的一致性渐近稳定无关,这与文[17-18]中相关结论一致.
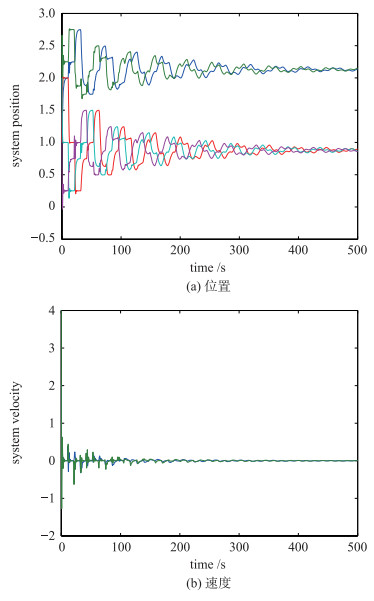
取通信时延h1=10,h2=20,输入时延T=0.44.异质多智能体系统中智能体的状态轨迹如图 3所示,可以看出二阶智能体组的位置收敛至2.14,速度收敛至0,一阶智能体组的位置收敛至0.87,相对于设定平衡点,产生了稳态误差,系统的收敛时间增大,从而说明时延的存在会影响系统的性能.
|
| 图 3 d=0,系统状态轨迹 Figure 3 The state trajectory of system with d=0 |
当d=0时即通信时延定常,可以运用类似文[18]处理一阶系统的频域方法,通过圆盘定理估计本例中的输入时延,得到T≤0.39,与之比较,本文定理2得出的结果保守性更小.当T=0.47 s时,系统等幅振荡,即系统的真实输入时延上界是T=0.47 s,与真实时延上界比较,定理2给出的输入时延上界保守了0.03.
(3)假定(2)中通信时延导数变为d1=d2=2,其它不变.根据推论2,调用LMI工具箱求解式(12),得到输入时延T≤0.17.
取通信时延η1(t)=10|sin(2t)|,η2(t)=20|sin(2t)|,输入时延T=0.17.异质多智能体系统中智能体的状态轨迹如图 4所示,系统收敛,但同样具有稳态误差.
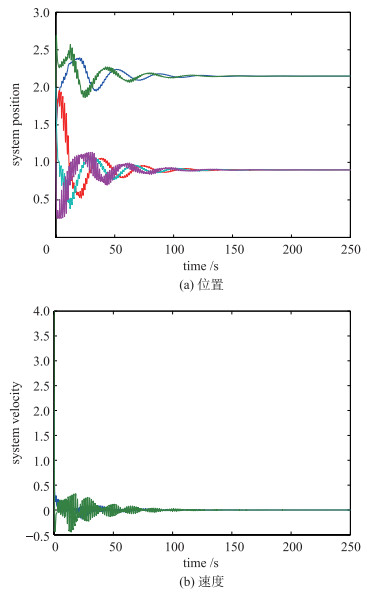
|
| 图 4 d1=d2=2,系统状态轨迹 Figure 4 The state trajectory of system with d1=d2=2 |
本文研究了同时具有时变通信时延和定常输入时延的异质多智能体系统的组一致性问题,提出了不依赖任何假设条件的一阶、二阶异质系统的组一致性算法,运用稳定性理论,给出了无时延系统实现静态组一致的k值范围.同时,以线性矩阵不等式的形式给出了时延系统实现静态组一致的充分条件,得出了输入时延的上界.通过计算机仿真发现,通信时延与系统的组一致性无关且时延的存在会影响系统的性能.本文仅以一阶、二阶异质系统为例,研究了二分组一致性问题,对于多个不同阶构成的异质系统多分组一致性问题是今后值得进一步研究的方向.
| [1] | Zheng Y S, Zhu Y, Wang L. Consensus of heterogeneous multi-agent systems[J]. IET Control Theory and Applications , 2011, 5 (16) : 1881–1888. DOI:10.1049/iet-cta.2011.0033 |
| [2] | Zheng Y S, Wang L. Consensus of heterogeneous multi-agent systems without velocity measurements[J]. International Journal of Control , 2012, 85 (7) : 906–914. DOI:10.1080/00207179.2012.669048 |
| [3] | 冯元珍, 屠小明, 李建祯. 一类异质多智能体系统的一致性控制[J]. 计算机应用 , 2013, 36 (6) : 1750–1752, 1758. Feng Y Z, Tu X M, Li J Z. Consensus control for a class of heterogeneous multi-agent systems[J]. Journal of Computer Applications , 2013, 36 (6) : 1750–1752, 1758. |
| [4] | 宋运忠, 谷明琴. 混合阶多智能体无向网络的拟平均一致性[J]. 控制工程 , 2009, 16 (2) : 220–222, 226. Song Y Z, Gu M Q. Quasi-average consensus in undirected networks of multi-agents with mixed order integrator[J]. Control Engineering of China , 2009, 16 (2) : 220–222, 226. |
| [5] | Liu C L, Liu F. Stationary consensus of heterogeneous multi-agent system with bounded communication delays[J]. Automatica , 2011, 47 (9) : 2130–2133. DOI:10.1016/j.automatica.2011.06.005 |
| [6] | 梁有明, 刘成林, 刘飞. 异质多自主体系统的一致性[J]. 系统工程学报 , 2012, 27 (5) : 583–592. Liang Y M, Liu C L, Liu F. Consensus of heterogeneous multi-agent systems[J]. Journal of Systems Engineering , 2012, 27 (5) : 583–592. |
| [7] | Dai P P, Liu C L, Liu F. Consensus problem of heterogeneous multi-agent systems with time delay under fixed and switching topologies[J]. International Journal of Automation & Computing , 2014, 11 (3) : 340–346. |
| [8] | Yu J Y, Wang L. Group consensus of multi-agent systems with undirected communication graphs[C]//Proceedings of the Asian Control Conference. Piscataway, NJ, USA:IEEE, 2009:105-110. |
| [9] | Feng Y Z, Xu S Y, Zhang B Y. Group consensus control for double-integrator dynamic multi-agent systems with fixed communication topology[J]. International Journal of Robust and Nonlinear Control , 2014, 24 (3) : 532–547. DOI:10.1002/rnc.v24.3 |
| [10] | Tan C, Liu G, Duan G. Group consensus of networked multi-agent systems with directed topology[C]//The 18th IFAC World Congress. Kington, UK:IFAC, 2011:8878-8883. |
| [11] | Godsil C, Royle G. Algebraic graph theory[M]. Berlin, Germany: Springer-Verlag , 2001 . |
| [12] | Shang Y L. Average consensus in multi-agent systems with uncertain topologies and multiple time-varying delays[J]. Linear Algebra and its Applications , 2014, 459 (15) : 411–429. |
| [13] | 宋莉, 伍清河. 具有时延和不确定拓扑的二阶多智能体系统的平均一致性[J]. 控制理论与应用 , 2013, 30 (8) : 1047–1052. Song L, Wu H Q. Average consensus of second-order multi-agent systems with time-delays and uncertain topologies[J]. Control Theory & Applications , 2013, 30 (8) : 1047–1052. |
| [14] | Olfati S R, Murray R M. Consensus problems in networks of agents with switching topology and time delays[J]. IEEE Transactions on Automatic Control , 2004, 49 (9) : 1520–1533. DOI:10.1109/TAC.2004.834113 |
| [15] | Sun Y G. Average consensus in networks of dynamic agents with uncertain topologies and time-varying delays[J]. Journal of the Franklin Institute , 2012, 349 (3) : 1061–1073. DOI:10.1016/j.jfranklin.2011.12.007 |
| [16] | Hale J K, Verduyn S M, Lune L. Introduction to functional differential equations[M]. Berlin, Germany: Springer , 1993 . |
| [17] | 梁有明, 刘成林, 刘飞. 具有通信时延和输入时延的1阶多自主体系统的一致性问题[J]. 信息与控制 , 2012, 41 (1) : 14–21. Liang Y M, Liu C L, Liu F. Consensus problem of first-order multi-agent systems with communication delay and input delay[J]. Information and Control , 2012, 41 (1) : 14–21. |
| [18] | Ji L H, Liao X F. Consensus problems of first-order dynamic multi-agent systems with multiple time delays[J]. Chinese Physics B , 2013, 61 (15) : 50–55. |



