1 引言
挠性欠驱动航天器是指独立控制的输入个数少于航天器自由度个数的挠性航天器.由于恶劣复杂的太空环境,航天器在长期运行后难免会产生故障,其中执行器的故障较为常见,执行器故障主要包括:部分失效、卡死、完全失效、饱和及驱动符号不确定等,而欠驱动航天器即是航天器的执行器发生完全失效故障.而对于一些小型的航天器而言,由于其体积、质量和成本的限制,往往不可能像大型航天器一样为提高其可靠性而增加冗余的执行器,在保证其姿态任务能够顺利完成的前提下,减少执行器的数量显得很有价值.而且现代的航天器根据不同的任务而附着了许多特定的挠性结构,如太阳能帆板、机械臂等,当航天器遇到外界干扰时,挠性结构会产生弹性形变,使得航天器的姿态发生变化,导致其姿态控制系统的不稳定.综合上述的因素,对于挠性欠驱动航天器的姿态控制问题变得越来越重要,且对该方向的研究也越有特殊的实际意义.
早在1983年,Crouch[1]对刚体欠驱动航天器姿态系统的可控性进行了研究,得到了以推力器为执行机构的航天器在不同的控制输入下,系统全局可控的充要条件. Byrnes[2]研究了欠驱动系统的可镇定性,研究表明,由于欠驱动系统不满足Brockett必要条件[3],仅有两个控制输入的刚体航天器不能够由连续定常的状态反馈控制律来实现渐近稳定. Casagrande等[4]针对欠驱动刚性航天器的角速度和姿态的渐近稳定问题,提出了一种时变切换控制律,但是这种方法在误差存在时可能会不满足切换条件,容易发散;Tsiotras和Corless等[5-6]都引入了周期项,从而设计了局部稳定的时变控制律;Morin和Samson利用平均原理和李亚普诺夫方法,研究出一个连续时变的控制器[7],可以局部指数稳定刚性航天器的姿态;戈新生和张彦琴等[8]利用齐次控制方法,针对刚性欠驱动航天器的姿态问题设计了稳定的反馈控制律.此外,Xiao和Hu等[9-10]利用滑模变结构的容错控制方法研究了挠性航天器在全驱动条件下的姿态稳定问题;Yang[11-12]和Aguiar[13]分别研究了挠性航天器在间歇性故障条件下和刚性欠驱动航天器的姿态稳定问题,提出了切换控制的思想,但是切换信号的选择与设计具有一定的难度;Wang和Jia针对单推力器航天器的姿态控制系统的可控性问题进行了研究[14],得出如果3个惯性主轴的转动惯量满足一定的条件可以实现航天器的姿态稳定;Ma和Jiang等[15]利用自适应补偿技术针对存在失控故障的挠性航天器姿态控制系统,设计了自适应容错控制律,实现航天器姿态和角速度的跟踪控制;Kim[16-17]和Huang[18]针对欠驱动航天器的姿态控制系统,采用分段解耦的控制思想,经过多次机动实现航天器三轴姿态稳定;张爱华等[19]将存在参数不确定的航天器姿态控制系统转换成一个级联系统,提出了一种有限时间渐近稳定策略,实现了航天器姿态的镇定控制.
齐次系统[20-23]是指系统的向量场具有齐次性,这种向量场的齐次性可以保证解空间和解空间上的单位闭球存在的一种映射关系,因此整个解空间就可以看做是该单位闭球的一种扩张.利用齐次系统的理论和齐次反馈概念构造的非光滑控制律在原点外光滑并且具有某种齐次性质,使得闭环系统指数收敛到平衡点.容错控制是指系统对故障的容忍能力,Jiang等[24]针对一类非线性系统提出了一种故障诊断与容错控制方法,使得系统在发生可接受的故障时仍能正常工作.
在文[8]和文[13]中,Ge和Aguiar均针对刚性欠驱动航天器的姿态控制系统,设计不连续的控制律实现姿态的渐近收敛性能,但并未考虑航天器上所附着的挠性模态,没有考虑二者之间的耦合;而在文[15]中,Ma针对挠性航天器的姿态控制系统,采用自适应的方法对未知的挠性模态进行参数化并进行有界估计,但是所考虑的故障模式为失控故障,并没有考虑完全失效故障.
因此,本文研究了挠性欠驱动航天器的姿态稳定问题,即在刚性欠驱动航天器的基础上加入挠性模态,使得此控制方法更接近于实际情况,便于理论的应用.因此本文具有以下3点创新和贡献:
(1)利用齐次系统的理论方法进行模型简化,降低系统的耦合程度.
(2)设计自适应观测器实现对剩余挠性非线性项的有界估计.
(3)针对简化系统,设计反馈容错控制律,实现航天器姿态和角速度的有界镇定控制.
在模型简化过程中,利用齐次性质忽略部分角速度与挠性模态和角速度与姿态之间的强耦合模态,降低了系统的复杂程度,便于观测器和控制律的设计;针对模型中不可忽略的非线性模态,设计自适应观测器实现对其结构的有界估计,便于控制律设计时对其进行补偿;针对简化后的模型,设计反馈容错控制律,并利用李亚普诺夫稳定性分析方法证明了该容错控制器能够实现对航天器姿态的有界稳定控制,仿真结果表明了该方法的有效性.
2 问题描述本节包括两部分:齐次系统的定义及其性质和挠性欠驱动航天器的角速度系统的问题提出.
2.1 齐次系统首先给出扩张算子的定义:
定义1[21] 对于任意的正常数ri>0,存在λ>0使得扩张算子δλ满足:
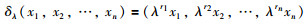
|
(1) |
那么ri称为扩张的权重.
齐次性可以利用上述的扩张算子进行定义:
定义2[21] 函数h:Rn→R称为关于扩张算子δλ的齐次函数且齐次的度为k,如果存在常数k∈R满足:
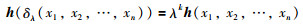
|
(2) |
向量f:Rn→Rn关于给定扩张算子δλ是齐次的且齐次的度为k,如果第i个分量是齐次函数且度为ri+k∈R,即满足:
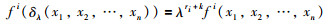
|
(3) |
其中fi是向量f的第i个分量.
根据上述的定义给出一些齐次函数的性质:
引理1[22] 向量f是关于扩张算子δλ的齐次向量且度为k,如果向量g满足:
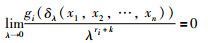
|
(4) |
如果系统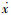
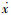
问题的提出包括挠性航天器的动力学模型、姿态运动学模型和控制目标.
2.2.1 动力学模型如果不考虑外界的干扰和系统的不确定性,则挠性欠驱动航天器的动力学方程可以表示为[9]:
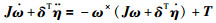
|
(5) |
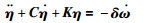
|
(6) |
其中,ω∈Ω⊂R3=[ω1,ω2,ω3]T是航天器主体的惯性角速度矢量;J=diag(J1,J2,J3)表示航天器总的惯性;T代表航天器的推力器所产生的控制力矩;η∈RN是弹性振动模态的坐标向量;δ∈RN×3是航天器刚性部分与挠性部分的耦合矩阵且满足列向量相互正交;矩阵C=diag(2ξiΛi)和K=diag(Λi2),i=1,…,N,分别代表航天器的阻尼矩阵和刚度矩阵,Λi和ξi分别为自然频率和阻尼系数;ω×是反对称矩阵,形式为:
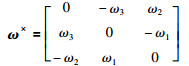
|
将方程(6)代入方程(5),方程(5)变为
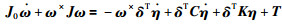
|
(7) |
其中J0=J-δTδ代表航天器刚性主体的惯性矩阵.不失一般性,令T3=0,其中T3是航天器推力器所产生的力矩在Z轴上的分量,则上述的动力学模型可以表述为
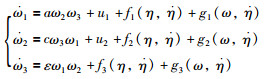
|
(8) |
式(8)中,
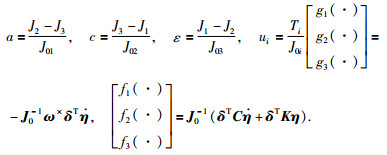
|
注1 航天器第j个推力器的执行器故障模型可以描述为[18]
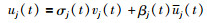
|
其中,σj∈[0, 1]是执行器的未知失效因子,表示乘性故障的时间分布;βj是未知函数,表示加性故障的时间分布;vj是执行器的控制信号;uj表示加性故障.
当σj(t)=1且βj(t)=0时,执行机构未发生任何故障;当σj∈(0,1)时,执行机构发生部分失效故障;当σj(t)=0时,执行机构发生完全失效故障;而卡死故障可以表述为σj(t)=0且uj=uj0.
针对航天器执行器故障的动力学模型(8),在全局范围内做如下假设:
假设1 航天器刚性部分和挠性部件耦合矩阵δ,挠性附件振动模态η及其导数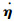
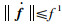
注2 由于现代航天器的挠性附件主要由先进材料构成,具有一定的阻尼特性.因此挠性附件的振动不会太大,而且其振动速率也是很小的,故上述假设是合理的.
2.2.2 运动学模型(w,z)参数描述是一种描述姿态的新方法,它通过2次垂直旋转,引入复变量,将球面上的点向复平面投影,来描述卫星的姿态,补充了3次旋转的欧拉角描述和一次旋转的四元数描述的完整性.用(w,z)参数其描述的姿态运动学方程w和z相互解耦可以分别控制,常被用在研究欠驱动航天器姿态控制的问题中.
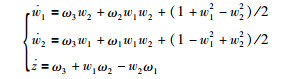
|
(9) |
其中w1、w2和z代表航天器的姿态参数.
2.2.3 控制目标通过分析挠性欠驱动航天器的动力学模型和运动学模型可以看出,欠驱动轴的角加速度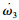
本文的控制目标可以表述为:针对存在执行器故障的挠性航天器姿态控制系统(8)、(9),设计控制律u1和u2实现对姿态的稳定控制,即当t→∞时,航天器的姿态(w,z)和角速度ω收敛于包含平衡点的任意小的邻域内.
注3 由于控制律u1和u2可以实现对角速度分量ω1和ω2任意跟踪控制,因此在后续的控制律设计过程中,令ω1和ω2为航天器姿态和欠驱动轴角速度ω3的控制输入,即设计期望角速度ω1和ω2使得航天器的姿态和角速度达到稳定状态.
3 控制器设计本节包括以下3部分内容:首先利用齐次系统的性质简化姿态系统模型;然后设计观测器实现对非线性耦合项的估计;最后设计反馈控制器,并给出系统的稳定性分析.
3.1 系统模型简化考虑航天器角速度子系统(如式(8)所示),还可以表示为下面的形式:
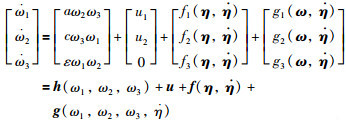
|
(10) |
引入如下的扩张算子:
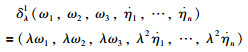
|
根据定义2可以得知,向量h是齐次的且度为1.再根据引理1,向量g满足如下性质:
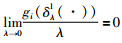
|
因此可以将向量g忽略,则角速度子系统(8)变为
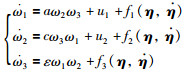
|
(11) |
本文将重点放在下面的子系统上,此系统忽略了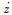
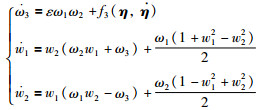
|
(15) |
还可以写为如下的紧凑形式:
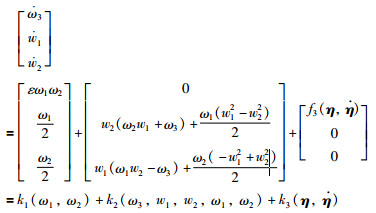
|
类似的,引入如下扩张算子:
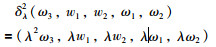
|
根据定义2很容易看出k1是齐次的且度为0.根据引理1,k2满足如下性质:
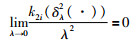
|
因此k2可以忽略.那么系统(12)可以简化为
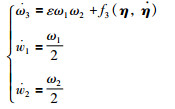
|
(13) |
在系统模型(13)中,忽略了姿态与角速度的耦合项,使得系统的复杂程度得到简化.可以说明k2对k1和k3的影响较小,可以忽略.该方法首次针对挠性欠驱动航天器的姿态控制系统进行简化,不仅可以降低控制器的设计难度,还可以提高航天器推力器的使用寿命.
3.2 自适应观测器设计针对角速度子系统(11),式中存在未知非线性项,设计自适应观测器估计系统中的未知信息,观测器的形式如下所示:
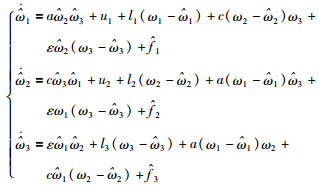
|
(14) |
其中, l1、l2和l3是正常数.
定义角速度和未知非线性项的误差为
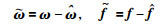
|
则误差系统可以写为
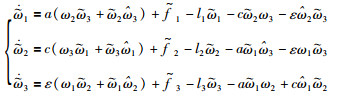
|
(15) |
设计对未知信息的自适应更新算法为
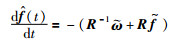
|
(16) |
其中, R=RT是正定对称矩阵.
定义变量及常数矩阵为
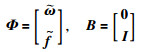
|
则误差系统(15)和更新算法(16)可以改写为
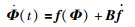
|
(17) |
引理2 针对系统(11),在假设1成立的情况下,设计观测器的形式为式(14)及自适应更新算法式(16),则系统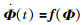
证明 选择如下的正定李亚普诺夫函数:
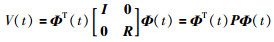
|
(18) |
其中, 矩阵R在更新算法(16)中给出.那么:
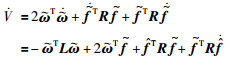
|
代入式(16)的更新算法,可以得到:
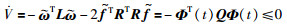
|
其中正定矩阵Q为
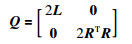
|
因此,系统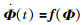
定理1 针对式(11)的系统,满足假设1的条件,设计式(14)形式的观测器及式(16)形式的更新算法,则观测误差Φ范数有界,且满足:
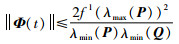
|
其中λmax和λmin分别表示矩阵最大和最小的特征值.
证明 根据引理2,系统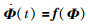
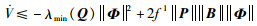
|
其中||B||=1,由于满足:
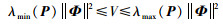
|
可以得到:
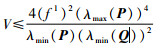
|
因此定理1成立.证毕.
注4 定理1中系统状态误差和非线性项的误差是一致范数有界的,可以通过选择合适的矩阵P和Q,使得其范数界任意小.
3.3 反馈控制器设计为了简化模型且不失一般性,假设ε>0,利用如下变换重新定义变量:
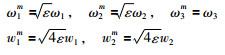
|
那么系统(13)可以改写为
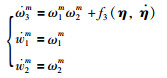
|
(19) |
简单起见,省略上角标m,除非另有说明,之后所有的操作都是针对系统(19).
定义新变量:
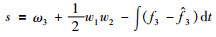
|
(20) |
提出一种新的初步控制律,形式如下:
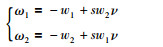
|
(21) |
其中,ν=ν(w1,w2,s)是待定的正定函数.
然后,s的导数可以写为
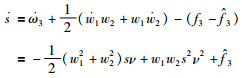
|
下面给出如下命题:
命题1 针对系统:
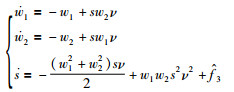
|
(22) |
设计控制律(21),满足ν>0且1-|s|ν≥0,可以保证系统(22)的状态有界.
证明 根据定理1,命题1可以转化为证明系统:
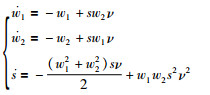
|
(23) |
的稳定性,即系统(23)渐近稳定,则系统(22)有界稳定.
选择正定李亚普诺夫函数如下:
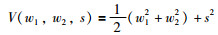
|
那么,其导数为
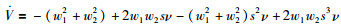
|
显而易见,以下不等式成立:
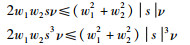
|
进而可以得到:
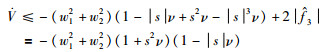
|
由定义ν>0可知1+s2ν>0.由于不等式1-|s|ν≥0成立,则系统(23)是渐近稳定的,根据定理1可以得到,系统(22)是有界稳定的.
上述结论表明,若控制律(21)是合理的,需要找到正函数ν使得满足1-|s| ν≥0,下面对未知函数ν进行设计.
命题2 选择正函数ν形式为
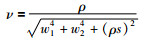
|
(24) |
其中ρ是常数且满足ρ>0.
证明 显而易见,由ρ>0可以得到ν>0成立.为了说明1-|s |ν≥0也是成立的,给出下面一组不等式:
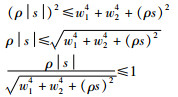
|
上述不等式表明1-|s|ν≥0成立.注意,上述不等式是严格成立的,除非w1和w2同时为0.要利用特定的函数ν完成命题2中的稳定性证明,还需要给出变量s的收敛特性,即当s趋于0时,系统(22)是稳定的.为了证明其成立,首先引入如下的比率:
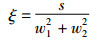
|
将上式对时间进行求导可得:
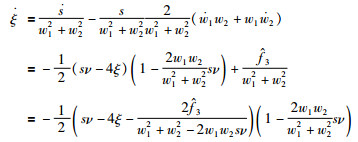
|
由于1-|s|ν≥0且|2w1w2|≤|w12+w22|,可以得出不等式:
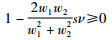
|
恒成立.那么注意:
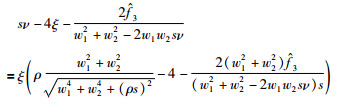
|
由于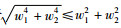
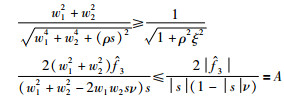
|
则上述过程证明如果:
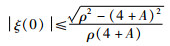
|
(25) |
成立,那么变量s是收敛的.证毕.
注5 不等式(25)说明比率ξ的初值不能太大,尽量接近于零点.因为参数A在航天器系统运行过程中可能会较大,当s趋于0时,A可能会趋于无穷,故ξ的初值选取尽量靠近零点.
注6 比率ξ的初值条件是容易满足的.即在初始时刻变量s的值足够小或者为0.那么只需要选择合适的ω和(w,z)初值,满足2ω3+w1w2=0,且w12(0)+w22(0)≠0即可,故比率ξ的初值条件(25)是容易满足的.
基于上述的分析,可以得到如下结论:
定理2 在假设1成立的条件下,式(19)描述的系统可以通过式(21)的反馈控制律实现有界稳定,控制律中变量s和函数ν分别如式(20)和式(24)所示且比率ξ的初值满足不等式(25),即当t→∞时,航天器的姿态和角速度收敛于平衡点附近的一个小的邻域内.
注7 根据引理2和定理1可以得出,在控制律(21)的作用下,航天器的角速度和姿态可以收敛到平衡点附近的一个小邻域内,且该邻域的大小可以通过对所设计的控制参数P、Q及ρ的调节实现其任意小.
注8 定理2中反馈控制律是针对系统(19)和系统(22),其控制量是航天器驱动轴的角速度分量,由于驱动轴的角速度可以由推力器直接控制,即针对系统(8)和系统(9),可以设计控制量u1和u2,使得航天器的角速度跟踪式(21)的角速度分量,从而实现航天器的姿态和角速度稳定.
注9 上述的控制方法可以应用到其它轴为欠驱动轴的情况.本文所针对的对象并非完全轴对称的航天器,即欠驱动轴的角速度不需要是恒值或为零,若其它轴为欠驱动轴,那么只需采用驱动轴所对应的角速度分量为控制输入,设计反馈控制律实现航天器的姿态和角速度的有界稳定.
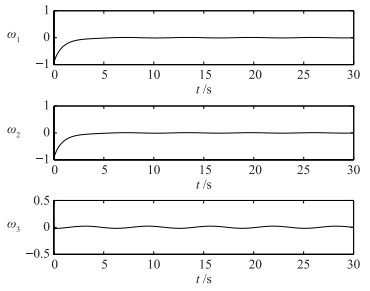
4 仿真分析本节针对某型挠性航天器的姿态控制进行了数值仿真.其中仿真参数ε=0.2,ρ=100.角速度的初值选取为ω1(0)=ω2(0)=0,ω3(0)=-0.125 rad/s;姿态的初值设置为w1(0)=w2(0)=0.5, z(0)=0.容易看出,航天器角速度和姿态的初值选取满足条件(25). 图 1~图 4分别为航天器姿态控制系统在控制律(21)作用下的角速度和姿态的轨迹变化曲线,图 1和图 2分别是简化系统模型(19)和(22)在控制律(21)的作用下的角速度和姿态变化轨迹;而图 3和图 4分别是原始系统模型(8)、(9)在控制律(21)的作用下的角速度和姿态变化轨迹.
|
| 图 1 简化模型的角速度变化轨迹 Figure 1 The trajectory of angular velocity of reduced model |
|
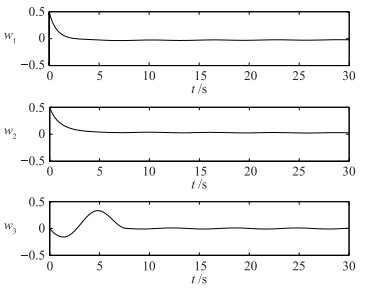
| 图 2 简化模型的姿态变化轨迹 Figure 2 The trajectory of attitude of reduced model |
|
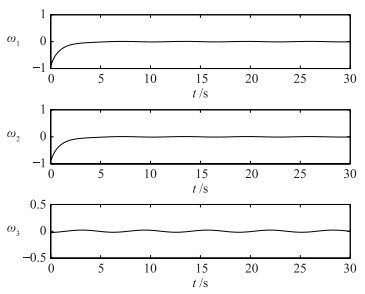
| 图 3 原始模型的角速度变化轨迹 Figure 3 The trajectory of angular velocity of original model |
|
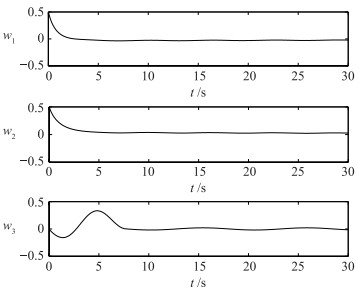
| 图 4 原始模型的姿态变化轨迹 Figure 4 The trajectory of attitude of original model |
图 1表明,针对航天器简化模型(19)、(22),在控制信号式(21)的作用下,驱动轴的角速度可以较快渐近收敛到平衡点,而欠驱动轴的角速度则收敛到平衡点附近的一个邻域内,从而实现航天器角速度的有界稳定控制;图 2为航天器的姿态变化情况,从图 2可以看出,航天器的姿态的收敛情况与角速度系统类似,即驱动轴的姿态可以实现渐近收敛到平衡点而欠驱动的姿态则收敛到平衡点附近的邻域内,从而实现航天器姿态的镇定控制;而控制信号(21)的变化曲线即为图 1中角速度ω1和ω2的变化轨迹曲线.
图 3表明,针对航天器原始模型(8)、(9),在控制信号(21)的作用下,航天器驱动轴的角速度仍可以较快收敛到平衡点附近,而欠驱动轴的角速度则收敛到平衡点附近的一个邻域内,从而实现航天器角速度的有界稳定控制;图 4为航天器的姿态变化情况,从图中可以看出,航天器的姿态的收敛情况与角速度系统类似,即驱动轴的姿态先收敛到平衡点附近而欠驱动的姿态则收敛到平衡点附近的邻域内,从而实现航天器姿态的镇定控制;而控制信号(21)的变化曲线即为图 3中角速度ω1和ω2的变化轨迹曲线.
经过比较,针对简化模型(19)、(22)所设计的反馈容错控制律(21)仍可以原始系统(8)、(9)有界稳定,从而说明利用齐次系统的理论和性质简化复杂的挠性航天器的姿态控制系统模型的方法是合理的,针对简化模型所设计的控制律也是有效的.
5 结论本文提出了一种新的方法实现对航天器复杂的姿态模型进行简化,即利用齐次系统的思想将系统中部分复杂的耦合项忽略掉,从而降低了控制器的设计难度.并设计了反馈容错控制器,此控制策略可以实现航天器角速度和姿态的镇定且收敛速度较快,控制信号的瞬态值不是很大,结果较为简单.将所提控制方法应用于某型挠性航天器的姿态控制系统,仿真结果验证了该方法的有效性.
| [1] | Crouch P E. Spacecraft attitude control and stabilization:Applications of geometric control theory to rigid body models[J]. IEEE Transactions on Automatic Control , 1984, 29 (4) : 321–331. DOI:10.1109/TAC.1984.1103519 |
| [2] | Byrnes C I, Isidori A. On the attitude stabilization of a rigid spacecraft[J]. Automatica , 1991, 27 (1) : 87–95. DOI:10.1016/0005-1098(91)90008-P |
| [3] | Brockett R W. Asymptotic stability and feedback stabilization[J]. Differential Geometric Control Theory , 1983, 27 : 181–191. |
| [4] | Casagrande D, Astolfi A, Parisini T. Global asymptotic stabilization of the attitude and the angular rates of an under-actuated non-symmetric rigid body[J]. Automatica , 2008, 44 (7) : 1781–1789. DOI:10.1016/j.automatica.2007.11.022 |
| [5] | Tsiotras P, Doumtchenko V. Control of spacecraft subject to actuator failures:State-of-the-art and open problems[J]. Journal of Astronautical Sciences , 2000, 48 (2) : 337–358. |
| [6] | Tsiotras P, Corless M, Longuski J. A novel approach for the attitude control of an axisymmetric spacecraft subject to two control torques[J]. Automatica , 1995, 31 (8) : 1009–1112. |
| [7] | Morin P, Samson C. Time-varying exponential stabilization of a rigid spacecraft with two control torques[J]. IEEE Transactions on Automatic Control , 1997, 42 (4) : 528–534. DOI:10.1109/9.566663 |
| [8] | 戈新生, 张彦琴. 欠驱动航天器姿态稳定性的齐次控制方法[J]. 北京信息科技大学学报 , 2014, 29 (1) : 1–5. Ge X S, Zhang Y Q. Homogeneous control of attitude stabilization for underactuated spacecraft[J]. Journal of Beijing Information Science and Technology University , 2014, 29 (1) : 1–5. |
| [9] | Xiao B, Hu Q L, Zhang Y M. Adaptive sliding mode fault tolerance attitude tracking control for flexible spacecraft under actuator saturation[J]. IEEE Transactions on Control Systems Technology , 2012, 20 (6) : 1605–1612. DOI:10.1109/TCST.2011.2169796 |
| [10] | Xiao B, Hu Q L, Zhang Y M. Fault-tolerant attitude control for flexible spacecraft without angular velocity magnitude measurement[J]. Journal of Guidance, Control, and Dynamics , 2011, 34 (5) : 1556–1561. DOI:10.2514/1.51148 |
| [11] | Yang H, Jiang B, Zhang Y M. Tolerance of intermittent faults in spacecraft attitude control:Switched system approach[J]. IET Control Theory and Applications , 2012, 6 (13) : 2049–2056. DOI:10.1049/iet-cta.2011.0453 |
| [12] | Yang H, Jiang B, Cocquempot V, et al. Spacecraft formation stabilization and fault tolerance:A state-varying switched system approach[J]. Systems and Control Letters , 2013, 62 (9) : 715–722. DOI:10.1016/j.sysconle.2013.05.007 |
| [13] | Aguiar A P, Hespanha J P, Pascoal A M. Switched seesaw control for the stabilization of underactuated vehicles[J]. Automatica , 2007, 43 (12) : 1997–2008. DOI:10.1016/j.automatica.2007.03.023 |
| [14] | Wang D X, Jia Y H, Jin L, et al. Controllability of an underactuated spacecraft with one thruster under disturbance[J]. Acta Mechanica Sinica , 2012, 28 (3) : 838–847. DOI:10.1007/s10409-012-0078-7 |
| [15] | Ma Y J, Jiang B, Tao G, et al. Uncertainty decomposition-based fault-tolerant adaptive control of flexible spacecraft[J]. IEEE Transactions on Aerospace and Electronic Systems , 2015, 51 (2) : 1053–1068. DOI:10.1109/TAES.2014.130032 |
| [16] | Kim D, Turner J D. Suboptimal continuous torque attitude maneuvers using two controls[J]. Journal of Guidance, Control, and Dynamics , 2013, 36 (6) : 1855–1859. DOI:10.2514/1.59903 |
| [17] | Kim D, Turner J D. Suboptimal continuous torque attitude maneuvers for underactuated spacecraft[J]. Aerospace Science and Technology , 2015, 40 : 104–108. DOI:10.1016/j.ast.2014.09.012 |
| [18] | Huang X H, Xu S J. Attitude control of an underactuated spacecraft based on piecewise decoupling method[J]. Journal of Astronautics , 2007, 28 (3) : 531–535. |
| [19] | 张爱华, 张志强, 霍星. 具有参数不确定性的航天器姿态有限时间稳定控制[J]. 信息与控制 , 2015, 44 (3) : 303–308. Zhang A H, Zhang Z Q, Huo X. Finite-time spacecraft attitude stabilization control subject to parameter uncertainties[J]. Information and Control , 2015, 44 (3) : 303–308. |
| [20] | Nakamura N, Nakamura H, Yamashita Y, et al. Homogeneous stabilization for input affine homogeneous systems[J]. IEEE Transactions on Automatic Control , 2009, 54 (9) : 2271–2275. DOI:10.1109/TAC.2009.2026865 |
| [21] | Moulay E. Stability and stabilization of homogeneous systems depending on parameter[J]. IEEE Transactions on Automatic Control , 2009, 54 (6) : 1382–1385. DOI:10.1109/TAC.2009.2015560 |
| [22] | Aleksandrov A Y, Kosov A A, Platonov A V. On the asymptotic stability of switched homogeneous systems[J]. Systems and Control Letters , 2012, 61 (1) : 127–133. DOI:10.1016/j.sysconle.2011.10.008 |
| [23] | Du H, Li S. Finite-time attitude stabilization for a spacecraft using homogeneous method[J]. Journal of Guidance, Control, and Dynamics , 2012, 35 (3) : 740–748. DOI:10.2514/1.56262 |
| [24] | Jiang B, Staroswiecki M, Cocquempot V. Fault accommodation for nonlinear dynamic systems[J]. IEEE Transactions on Automatic Control , 2006, 51 (9) : 1578–1583. DOI:10.1109/TAC.2006.878732 |



