2. 江南大学物联网工程学院, 江苏 无锡 214122
2. School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China
1 引言
无线传感器网络(wireless sensor network,WSN)[1]已经在军事、民用等领域有很多应用,包括环境监测[2]、网站安全[3]、医疗诊断[4]、战场监视[5]、灾害救助[6]和辅助生活[7]等.生活中很多应用与位置有关,无线传感器网络易于部署、可扩展性高、成本低等特点使其在室内定位中具有很大的优势.
无线传感器网络定位算法[8]通常可以分为基于测距[9-11]和无需测距[12-13]两类.前者需要获取目标与参考节点之间的距离或者角度信息,一般需要额外的硬件支持;后者仅需要获取目标与参考节点之间的网络连通度等信息实现节点之间的定位,计算简单且易于实现,但是定位精度较低[14].
基于接收信号强度指示(received signal strength indication,RSSI)的定位方法成本低,定位精度较高,但是在实际环境中容易受到反射、多径传播、天线增益和障碍物阻隔等因素的影响,质心算法简单、容易实现,但是定位精度较基于RSSI的方法偏低.在采用RSSI进行测距的方法中,大都是利用相关的模型建立RSSI和距离之间的关系曲线,得到RSSI和距离之间的函数关系式[15],或者是采用一定的方法建立RSSI和距离之间的映射关系数据库[16].然而,无线电波在实际的传播过程中,RSSI和距离间的点对点的对应关系存在较大误差,去掉RSSI中的极大极小值,利用最大似然估计降低RSSI和距离关系之间的误差.
质心算法使用包含定位信息的锚节点的质心作为估计节点的位置,完全基于网络连通性,算法简单且易于实现.但定位精度与锚节点的密度以及分布有很大关系.当前有许多关于质心算法改进方法的文章,尤其在基于RSSI技术和质心算法方面对定位改进研究比较多:文[17]将RSSI测距技术得到的距离的倒数作为改进后质心算法的权系数.该算法在传统质心定位算法基础上,加入距离因子作为权重因子,较传统质心算法对定位精度有很大的提高,但是测距造成定位结果随机性很大,造成定位结果估算误差大和误差累积严重的现象.文[18]在距离加权的质心算法基础上提出一种利用节点之间的RSSI代替距离来加权的方法,定位精度有很大提高.文[19]通过节点之间相对位置关系对锚节点进行编组,权值以组的形式出现,然而现实环境中RSSI波动较大,如果不对信号进行处理,容易造成定位不稳定的现象.
上述的质心算法都是在锚节点分布均匀的情况下进行改进,在一定程度上提高了定位的精度,但增加了定位的成本,对于一些特殊环境不能有效地应用.本文的锚节点都是随机分布在定位区域.为了降低测距误差和定位成本,本文利用测量距离的最大似然估计,并通过引进参数,提出了基于最大似然估计的加权质心算法.通过距离之间的估计关系和信号极大极小值的处理,来减少信号反射和多径效应等因素对定位造成的干扰.引进参数模型优化锚节点分布.结果表明,在10 m×10 m、50 m×50 m和100 m×100 m区域,提出的算法与现有的质心算法相比,定位精度有明显地提高.
2 质心定位算法 2.1 传统的质心定位南加州大学的Bulusu等[20]提出一种基于网络连通性无需测距的质心定位算法,其主要思想是:未知节点以所有在其通信范围内锚节点的几何质心作为自己的估计位置.其未知节点的位置为
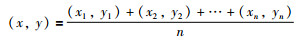
|
其中,(x1,y1),(x2,y2),…,(xn,yn)是锚节点的坐标.传统的质心定位算法具有成本低、计算量小、原理简单易于实现的优点,但是定位精度对于节点的密度依赖大,精度较低.
2.2 加权的质心定位在很多情况下,目标位置并不是严格意义上周围锚节点的实际质心,为了提高质心算法的定位精度,对算法进行加权
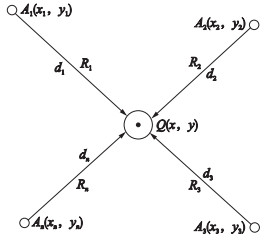
如图 1所示,把RSSI转化为距离,距离由小到大3个为一组权值[17] 

|
| 图 1 质心算法的示意图 Figure 1 Schematic diagram of centroid algorithm |
对于无线传感器网络来说,在室内情况下RSSI受环境的影响程度非常大,同一个RSSI值,在同一网络拓扑分布中的不同节点对应的距离不同,相应的权值也不同.距离越近对定位影响越大,反之越远影响越小,这就需要对权值进行合理分配.质心定位是由多个锚节点对一个目标联合区域定位,如果不能把定位范围内的锚节点整体考虑,而只是针对个体加权,很难提高算法的定位精度.
3 改进后的质心定位算法 3.1 基于RSSI的测距模型在室内情况下,信号的反射、散射或者遮蔽现象通常会对接收者采集到的信号强度产生干扰,通常采用对数正态阴影模型(log-normal shadowing)[21]:

|
(1) |
其中,P0(d0)为参考节点d0处的信号强度,Pr(d)为在距离d处的未知节点的信号强度,η为路径损耗系数,通常取值在2~6之间. Xσ是标准差为σ、均值为0的高斯分布随机变量.当路径的损耗参数已知时,接收者可以通过接收到的信号强度来衡量自己与信号源之间的距离.假设信号数已知或可估计,在该模型下,接收者与信号源之间距离d的最大似然估计为

|
(2) |
通过以上计算得到接收者与信号源之间的距离与实际距离之间的关系为

|
(3) |
其中,


|
(4) |
由此可见,上述的最大似然估计是偏离真实距离的.无偏差的估计结果可以通过如下公式得到:
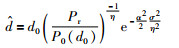
|
(5) |
在室内环境下,由于信号传播会给测距带来很大的干扰,当d0=1 m时,根据式(5)得出未知节点到锚节点之间的距离:

|
(6) |
其中,Ri,x是未知节点x到第i个锚节点的信号强度,P0(d0)表示未知节点1 m处的信号强度.把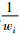
针对似然函数可能会出现多个局部最大值,为了获得全局收敛性进行适当的初始化.例如有N个信号源,当N=2时,先求出起始值d0(0),令只有一个源d0,则:

|
(7) |
而后求出d1(1).设第1个源位于d0(0),则:

|
(8) |
接着依次可求



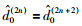


如果把RSSI作为质心定位的权值,信号会因为干扰出现很大的波动,无法很好地抑制这种随机性变化.为了解决RSSI的干扰和锚节点难以优化的问题,本文提出了一种新的加权模型.在这个加权模型中,既能够表现出锚节点对未知节点的接近程度,又能够在锚节点数少的情况下提高定位精度.本文引进一个参数k到加权模型中,合理的参数k能够有效地提高定位精度.
把


|
(9) |
本文所用的权值中参数k是一个引进变量,需要调整参数k提高定位精度.在实验中,以50 m×50 m作为实验区域,锚节点和未知节点都采用TI公司的CC2530通信模块且所有节点都是随机分布,参数选择k∈[2, 5]. 图 2、图 3为不同参数对应的定位误差变化曲线.在图 2中,当锚节点数为4时,可以看出在k=3和k=4的定位误差出现了一个突变,由于k=3.5时的误差小于k=3时的误差,得出参数k是一个靠近4但不等于4的值.从图 3中可以看出,当锚节点数为5时,k=4.6时的误差小于k=4.8时的误差.

|
| 图 2 参数k∈[2,4]的定位误差曲线 Figure 2 Position error curves when parameter k∈[2, 4] |

|
| 图 3 参数k∈[4.2,5.0]的定位误差曲线 Figure 3 Position error curves when parameter k∈[4.2, 5.0] |
设置一个未知节点和7个锚节点随机分布在50 m×50 m的区域,且未知节点分布在500个不同的位置,路径损耗因素η=4,4.5,5,5.5,6[21],Xσ是标准差为σ、均值为0的高斯分布随机变量.仿真结果如表 1所示,基于此,本文在定位过程中得出的最优参数值为k=n-0.4.
因此,质心定位的权值可以改写为

|
(10) |
改进的质心算法定位步骤如下:
(1)在无线传感器网络定位区域,确定锚节点和未知节点随机分布在该定位区域;
(2)锚节点周期性向周围发送自身节点ID和位置信息;
(3)对于同一个未知节点收到信息后,只记录同一个锚节点的RSSI值,当接收到一定数量的RSSI值后,去掉其中的极大极小值,即min{Ri1,Ri2,…,Rin} < Rij < max{Ri1,Ri2,…, Rin}, 然后取均值作为接收到的RSSI值:

|
(11) |
其中,Rin表示第i个锚节点的n次信号强度,Ri表示第i个锚节点的信号强度均值.然后依次求出其它锚节点到未知节点的信号强度.
(4)利用信号的衰减模型,得到距离的最大似然估计,建立未知节点到锚节点之间的关系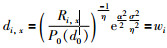
(5)引进参数k,构建一个周围锚节点数和锚节点到未知节点距离相关质心算法的权值
(6)通过实验,得到最优参数k=n-0.4;
(7)代入最优参数k,利用式(7)计算出目标的位置,为了得到更精确的位置,选取距离目标最近的3个锚节点通过上述方法分别进行定位,把得到的位置与已知位置作差求平均,即为修正值(Δx,Δy).最终的未知节点位置为(x0,y0)=(|x-Δx|,|y-Δy|).
4 实验结果与分析利用Matlab(R2010b)仿真软件对上述算法性能进行仿真验证.分别以10 m×10 m、50 m×50 m和100 m×100 m作为实验仿真的区域,仿真区域内所有节点都随机分布处于静止状态(如图 4所示)且节点之间通信正常,通信半径为30 m;路径损耗因素η=4.所有仿真实验环境中都加入均值为0、标准差为σ=4的满足高斯分布的随机噪声,仿真实验均进行300次,最后未知节点定位结果取平均值.

|
| 图 4 节点分布图 Figure 4 Distribution map of the nodes |
误差分析:

|
(12) |
其中,(x,y)表示未知节点的实际位置,(x0,y0)表示未知节点的估计位置.
本文通过与文[13]和文[17]的质心加权算法的定位精度的比较,来分析基于最大似然估计的加权质心算法的定位性能.仿真结果用WCL-d和WCL-RSSI分别表示基于距离和信号强度的加权定位,proposed WCL表示提出的质心加权算法.
4.1 未知节点定位误差图 5所示为未知节点的定位误差,选取100个未知节点随机分布在10 m×10 m的区域内,锚节点也是随机分布在该区域.从图中可以看出改进后的质心算法不但定位精度高而且稳定,不会因为周围环境复杂而造成较大误差,平均定位误差为0.2 m.

|
| 图 5 未知节点的定位误差 Figure 5 Location errors of the unknown nodes |
图 6可以看出在50 m×50 m的区域中,本文改进的质心算法优于其它2种质心算法,最大似然估计增加了锚节点到未知节点的权重,优化了锚节点的分布.在锚节点不多的情况下,仍保持较高的定位精度.当锚节点数量为7时,该算法的平均定位误差为0.24 m.

|
| 图 6 不同锚节点数量对应的定位误差曲线 Figure 6 Location error curves of different number of anchor nodes |
图 7描述了不同路径损耗参数对定位误差的影响. 100个未知节点随机放置在100 m×100 m区域,可以明显看出,合理的路径损耗参数对未知节点定位有很大的影响,当η=4时,定位误差最小.

|
| 图 7 不同路径损耗对应的定位误差曲线 Figure 7 Localization error curves vs. the path loss exponent |
由表 2可知,随着定位区域的增大,与其它2种算法相比定位精度都有明显的提高,而且该算法的定位误差没有显著的增大,具有较好的定位性能.
| 定位算法 | 10 m×10 m 平均定位误差 |
50 m×50 m 平均定位误差 |
100 m×100 m 平均定位误差 |
| 距离加权算法 | 1.61 m | 16.79 m | 37.13 m |
| 信号加权算法 | 0.43 m | 3.83 m | 6.63 m |
| 本文提出的算法 | 0.20 m | 0.23 m | 0.54 m |
在节点能耗承受的范围内,考虑到最大似然法的计算量很大,但是在样本数较少以及信号相关的情况下也能保持良好的性能[24].
综上所述,本文改进的定位算法在定位精度方面优于其它2种加权质心算法.提出的算法对锚节点的数量要求不是很高,在节点相对较少的情况下,仍具有较高的定位精度.
5 结论本文在研究大量的质心定位算法和基于RSSI定位算法的基础上,提出了一种基于最大似然估计的加权质心定位算法.新的加权模型有效地抑制了信号的干扰和优化了锚节点分布.对比不同规模的网络定位分析该算法的性能,仿真结果表明,该算法在定位精度方面优于其它两种质心算法,具有较好的网络拓展性,减少了对锚节点的需求,降低了定位的成本.
| [1] | 许驰, 郑萌, 梁炜, 等. 认知无线传感器网络的协作频谱感知[J]. 信息与控制 , 2015, 44 (4) : 430–435. Xu C, Zheng M, Liang W, et al. Cooperative spectrum sensing of the cognitive wireless sensor network[J]. Information and Control , 2015, 44 (4) : 430–435. |
| [2] | Paek J, Hicks J, Coe S, et al. Image-based environmental monitoring sensor application using an embedded wireless sensor network[J]. Sensors , 2014, 14 (9) : 15981–16002. DOI:10.3390/s140915981 |
| [3] | Debashis D. An integrated method for location registration of mobile terminals based on time, distance and zone[J]. Journal of Computational Intelligence and Electronic Systems , 2013, 2 (1) : 20–28. DOI:10.1166/jcies.2013.1045 |
| [4] | Anindita R, Debashis D. Intelligent body sensor network for pervasive health monitoring:A survey[J]. Journal of Computational Intelligence and Electronic Systems , 2012, 1 (1) : 67–81. DOI:10.1166/jcies.2012.1006 |
| [5] | Bokareva T, Hu W, Kanhere S, et al. Wireless sensor networks for battlefield surveillance[C]//Proceedings of the Land Warfare Conference, Brisbane, AUS:Biblio Quest International Pty Ltd, 2006:1-8. |
| [6] | Tuna G, Gungor V C, Gulez K. An autonomous wireless sensor network deployment system using mobile robots for human existence detection in case of disasters[J]. Ad Hoc Networks , 2014, 13 (SI) : 54–68. |
| [7] | 汪涛, 谢志军. 基于WSN的智能家居控制系统设计与实现[J]. 无线电通信技术 , 2015, 41 (2) : 71–75. Wang T, Xie Z J. Design and implementation of smart home control system based on wireless sensor network[J]. Radio Communication Technology , 2015, 41 (2) : 71–75. |
| [8] | 肖金超, 曾鹏, 何杰, 等. 基于传感器网络的多信道定位技术[J]. 信息与控制 , 2015, 44 (3) : 346–352. Xiao J C H, Zeng P, He J, et al. Multi-channel localization technology based on sensor networks[J]. Information and Control , 2015, 44 (3) : 346–352. |
| [9] | Ahn H, Rhee S B. Simulation of a RSSI-based indoor localization system using wireless sensor network[C]//2010 Proceedings of the 5th International Conference on Ubiquitous Information Technologies and Applications(CUTE). Piscataway, NJ, USA:IEEE, 2010:1-4. |
| [10] | Xu B, Sun G D, Yu R, et al. High-accuracy TDOA-based localization without time synchronization[J]. IEEE Transactions on Parallel and Distributed Systems , 2013, 24 (8) : 1567–1576. DOI:10.1109/TPDS.2012.248 |
| [11] | Wang Q H, Lu T T, Liu M L, et al. Research on the WSN node localization based on TOA[J]. Journal of Applied Mathematics, 2013, 2013, ID:706064:1-6. |
| [12] | He T, Huang C D, Blum B M, et al. Range free localization schemes for large scale sensor networks[C]//Proceedings of ACM International Conference on Mobile Computing and Networking. New York, NJ, USA:the ACM, 2003:81-95. |
| [13] | Fang W, Yang G. Improvement based on DV-Hop localization algorithm of wireless sensor network[C]//2011 International Conference on Mechatronic Science, Electric Engineering and Computer(MEC). Piscataway, NJ, USA:IEEE, 2011:2421-2424. |
| [14] | 衣晓, 刘瑜, 黄越平. 无线传感器网络Range-free自身定位算法仿真分析[J]. 海军航空工程学院学报 , 2009, 24 (4) : 369–375. Yi X, Liu Y, Huang Y P. Simulation and analysis of range-free self-localization algorithm in wireless sensor networks[J]. Journal of Naval Aeronautical and Engineering Institute , 2009, 24 (4) : 369–375. |
| [15] | Fang Z, Zhao Z, Geng D Q, et al. RSSI variability characterization and calibration method in wireless sensor network[C]//2010 IEEE International Conference on Information and Automation. Piscataway, NJ, USA:IEEE, 2010:1532-1537. |
| [16] | Huang W, Zhang Z H, Wang R B, et al. An adaptive distance correction localization algorithm based on RSSI for WSNs[M]//Lecture Notes in Electrical Engineering. Berlin, Germany:Springer, 2012:369-378. |
| [17] | 于慧霞. WSN中基于RSSI的加权质心定位算法的改进[J]. 电子测试 , 2012, 32 (7) : 28–32. Yu H X. Weighted centroid localization algorithm with weight corrected based on RSSI for wireless sensor network[J]. Electronic Test , 2012, 32 (7) : 28–32. |
| [18] | Zhang Z H, Chen D. An improved RSSI-based centroid localization algorithm in wireless sensor networks[C]//2011 International Conference on Computer Science and Service System(CSSS). Piscataway, NJ, USA:IEEE, 2011:3008-3011. |
| [19] | 李文辰, 张雷. 无线传感器网络加权质心定位算法研究[J]. 计算机仿真 , 2013, 30 (2) : 191–194. Li W C, Zhang L. Research on weighted centroid location algorithm for wireless sensor network[J]. Computer Simulation , 2013, 30 (2) : 191–194. |
| [20] | Bulusu N, Heidemann J, Estrin D. Adaptive beacon placement[C]//21st International Conference on Distributed Computing Systems. Piscataway, NJ, USA:IEEE, 2001:489-498. |
| [21] | Seidel S Y, Rappaport T S. 914 MHz path loss prediction models for indoor wireless communications in multi-floored buildings[J]. IEEE Transactions on Antennas & Propagation , 1992, 40 (2) : 207–217. |
| [22] | 杨峥, 吴陈沭, 刘云浩著. 位置计算:无线网络定位与可定位性[M]. 1版. 北京: 清华大学出版社 ,2014 : 6 -8. Yang Z, Wu C S, Liu Y H. Location-based computing:localization and localizability of wireless networks[M]. 1st ed. Beijing: Tsinghua University Press , 2014 : 6 -8. |
| [23] | Heurtefeux K, Valois F. Is RSSI a good choice for localization in wireless sensor network[C]//26th IEEE International Conference on Advanced Information Networking and Applications. Piscataway, NJ, USA:IEEE, 2012:732-739. |
| [24] | 田孝华, 周义建. 无线电定位理论与技术[M]. 1版. 北京: 国防工业出版社 ,2011 : 128 -130. Tian X H, Zhou Y J. Theory and technology of wireless location[M]. 1st ed. Beijing: National Defense Industry , 2011 : 128 -130. |



