文章快速检索  
  高级检索
引用本文
刘春平, 王昕, 王振雷. 基于多模型混合的广义最小方差控制性能评估[J]. 信息与控制, 2016, 45(5): 588-592, 599.
LIU Chunping, WANG Xin, WANG Zhenlei. Performance Assessment of Control Systems Based on a Multiple-model Mixing Method with Generalization Minimum Variance[J]. Information and Control, 2016, 45(5): 588-592, 599.
基于多模型混合的广义最小方差控制性能评估
刘春平1, 王昕2, 王振雷1     
1. 华东理工大学化工过程先进控制和优化技术教育部重点实验室, 上海 200237 ;
2. 上海交通大学电工与电子技术中心, 上海 200240
收稿/录用/修回: 2015-09-24/2015-01-29/2016-03-17
基金项目: 国家973资助项目（2012CB720500）；国家自然科学基金资助项目（61333010，61134007）；上海市科委资助项目（13111103800）；上海市自然科学基金资助项目（14ZR1421800）；流程工业综合自动化国家重点实验室开放课题基金（PAL-N201404）
作者简介: 刘春平（1991-），男，硕士生．研究领域为控制系统性能评估.
王昕（1972-），男，博士，副教授．研究领域为多模型自适应控制，智能解耦，复杂工业过程建模、控制与优化.
通讯作者: 王振雷（1975-），男，博士，教授．研究领域为智能控制，复杂系统的建模及特征分析，故障诊断，智能优化算法．wangzhen_l@ecust.edu.cn
摘要: 针对实际工业过程中控制系统经常会受到时变扰动的影响，致使针对单一扰动模型设计的性能评估方法不再适用于时变扰动控制系统的问题，提出了基于多模型混合的广义最小方差控制性能评估方法．该方法综合考虑被控对象输出方差与控制器输出方差的两个指标，同时提出了一种“判断—加权”的控制器设计策略．首先，在任一时间段选取使广义输出方差最小的控制器，并判断其与上一时间段采用的控制器是否一致；然后，在此基础上采用多模型混合思想进行控制器设计，并将其作用下的广义输出方差作为性能评估的基准．通过乙烯裂解炉仿真，验证了本文所述方法在时变系统性能评估中的有效性．
关键词: 广义最小方差     多模型     判断-加权     性能评估    
Performance Assessment of Control Systems Based on a Multiple-model Mixing Method with Generalization Minimum Variance
LIU Chunping1, WANG Xin2, WANG Zhenlei1     
1. Key Laboratory of Advanced Control and Optimization for Chemical Processes, East China University of Science and Technology, Shanghai 200237, China ;
2. Center of Electrical & Electronic Technology, Shanghai Jiao Tong University, Shanghai 200240, China
Abstract: Almost all control loops in industry are under the influence of time-variant disturbances. Performance assessment based on a single model of disturbance is not sufficient for such systems. To solve this, we propose performance assessment of control systems based on a multiple model mixing method with generalized minimum variance. A trade-off is made between the manipulated variable variance and the controller output variance, and the strategy of judgement-weighting is proposed. First, the controller with the minimum generalized variance is chosen and the judgment made as to whether it is different from the previous chosen controller in each period. Then, based on the chosen controllers, a benchmark controller is obtained with the multiple models mixing method. Finally, the generalized variance of the control system under the effect of the benchmark controller serves as the standardwith which to assess a system with time-variant disturbances. Simulation of an ethylene-cracking furnace demonstrates that the proposed method can be applied to control systems with time-variant disturbances.
Key words: generalized minimum variance     multiple model     judgement-weighted     performance assessment    

1 引言

随着实际工业过程自动化程度的不断提高，控制系统的控制回路不断增多.工业过程普遍存在大量控制回路.在控制器运行的初期，控制系统往往运行状态良好，但由于操作点变化、执行机构老化等各种因素的影响，控制系统的性能会逐渐下降，不能维持在理想的运行状态.因此，根据过程数据对控制系统进行性能评估并在此基础上进行控制策略改进，对企业经济效益的提升至关重要.

控制系统性能评估最早由Harris在1989年提出来[1]，得到了广泛的关注与发展. Huang等针对反馈控制系统、前馈控制系统等提出了完整的基于最小方差的控制系统性能评估方法[2].基于最小方差的控制系统性能评估方法是以控制系统输出方差为基准并在此基础上对过程控制系统进行性能评估的.然而，在工业过程中，控制器输出的波动对整个控制系统的稳定性与能耗有着至关重要的影响.为此，Rubens等采用控制器输出惩罚策略，提出了广义最小方差控制器的设计方法[3].在此基础上，文[4]首先提出将广义最小方差作为控制系统性能评估的基准，以对时不变扰动系统的控制性能进行评估.此后，文[5]将基于广义最小方差的基准推广到非线性前馈—反馈控制系统中.文[6]将广义最小方差基准推广到并行串级控制系统中.文[7-8]基于广义最小方差的控制性能评估方法提出了控制器自整定方法.文[9]将基于广义最小方差的控制性能评估方法从单变量系统推广到了多变量系统.

在时变扰动系统中，通常在不同时间段采用不同的扰动模型表征时变扰动的特性，这为基于模型的时变扰动控制系统性能评估提供了基础.文[10]研究了单变量时变扰动系统的瞬态扰动问题，提出了一种针对最具代表性扰动的时变扰动控制性能评估方法.文[11]又在文[10]的基础上提出了改进的时变扰动控制系统性能评估方法.文[12]对具有时变扰动的PID(proportional-integral-derivative)控制系统进行了性能评估研究.然而，对于如何评估具有多个扰动时的系统控制性能的相关研究较少.文[13-14]指出多模型方法能有效解决具有多个扰动的控制系统的控制问题.为解决具有多个时变扰动的控制系统性能评估问题，Yoshihiro等将多模型切换的思想引入到控制系统性能评估中，提出在每一时间段根据扰动模型直接设计控制器、不同时间段控制器进行切换的控制策略[15-16].然而，在实际工业过程中，当控制器参数在不同数值之间切换时，控制器输出会产生跳变，导致控制系统输出产生暂态误差.暂态误差无法根据过程数据预测得到，因而严重影响基于多模型切换策略的控制系统性能评估结果的准确性[17-18].为此，张巍等提出基于多模型混合策略，以控制系统输出最小方差为基准，对具有多个时变扰动的控制系统进行了控制性能评估，有效地解决了多模型切换策略存在的暂态误差问题[19-20].但文[19-20]方法并未考虑控制器输出波动对控制系统性能评估的影响.如何综合考虑控制系统输出方差与控制器输出方差对时变扰动控制系统性能评估的影响，并在此基础上设计新的性能评估基准尚需进一步研究.

为此，本文将多模型混合策略与广义最小方差控制器设计准则结合，提出了基于多模型混合的广义最小方差控制性能评估方法.首先根据每个扰动模型设计广义最小方差控制器；然后在每一时间段选择使广义方差达到最小的控制器，并判断该控制器与上一时间段的控制器是否相同：若相同，则控制器不变；如果不同，则基于扰动的作用时间获取权重以对前后两个控制器进行加权，实现控制器缓慢变化并最终切换到该时间段选取的最优控制器上.通过乙烯裂解炉仿真，验证了本文所述方法在时变扰动控制系统性能评估中的有效性.

2 被控对象描述

被控对象输入扰动均可通过乘以被控对象传递函数变换为被控对象输出扰动.故本文具有多个扰动的单变量闭环回路控制系统框图可用图 1表示.

图 1 多个扰动的闭环控制系统框图 Figure 1 Block diagram of closed loop control system with multiple disturbances
图选项

在图 1中，被控对象存在n个时变扰动.若第i个扰动的作用时间区间为Mi，则t时刻被控对象的所有扰动表示为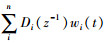，其中，当t∉Mi时，Di(z-1)=0.根据每个扰动的作用时间将过程划分为T1，T2，…，Tm时间段且Ttotal=∪Tj(j=1，2，…，m). A(z-1)、B(z-1)、Di(z-1)分别为z-1的多项式，r(t)为闭环回路的设定值，Q(z-1)为控制器离散传递函数，km为被控对象时滞，u(t)、y(t)分别为闭环回路在离散时间t的控制器输出与被控对象输出，wi(t)为均值为0、方差为1的白噪声序列.

3 基于多模型混合的广义最小方差控制性能评估

本文提出的多模型混合的思想是：首先根据每一扰动模型设计单个扰动的广义最小方差控制器；然后，闭环回路的理想控制器在此基础上通过“判断-加权”的方式得到，并将其作用下的广义输出方差作为性能评估的基准.

3.1 单个扰动的广义最小方差控制器设计

当单个扰动Di(z-1)作用于回路时，根据广义最小方差控制准则设计控制器.广义最小方差控制使如下形式的函数取值最小：

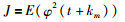
(1)

其中E为方差期望算子. ϕ(t+km)取如下形式：

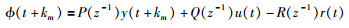
(2)
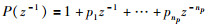
(3)
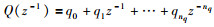
(4)
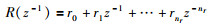
(5)

在通常情况下取r(t)=0，则：

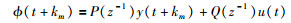
(6)

现有如下丟番图方程：

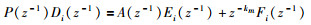
(7)
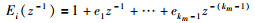
(8)
(9)

当单个扰动Di(z-1)作用于回路时，其满足的离散方程为

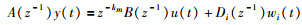
(10)

将式(7)代入式(10)，可得

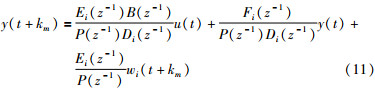
(11)

将式(11)代入式(6)，则式(6)在单个扰动下变换为

(12)

由于Ei(z-1)的阶次为km-1，则Ei(z-1)wi(t+km)总与其它部分相互独立，则：

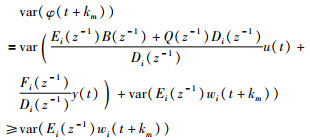
(13)

因此，根据式(13)可得到广义最小方差控制律：

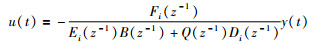
(14)

此时var(φ(t+km))=var(Ei(z-1)wi(t+km)).故根据单个扰动Di(z-1)设计的广义最小方差器为

(15)

此外，将Qi(z-1)作用下闭环回路的广义输出方差作为基于Di(z-1)的单模型性能评估方法的基准.

3.2 多模型混合的广义最小方差控制器设计

当多个时变扰动D1，D2，…，Dn作用于控制系统时，根据扰动作用时间可将过程依次划分为T1，T2，…，Tm时间段且Ttotal=∪Tj，j=1，2，…，m.根据每一扰动设计广义最小方差控制器Q1，Q2，…，Qn组成广义最小方差控制器集QI=｛Q1，Q2，…，Qn｝.在Tj时间段，从QI中选取使广义输出方差最小的控制器为该时间段的闭环控制器QTj(z-1).在输出与输入具有时间延迟的对象中，当上一时间段选取的控制器QTj-1(z-1)与当前时间段选取的控制器QTj(z-1)不同时，闭环回路控制器切换易导致控制器输出产生跳变，相当于给被控过程加入了一个额外的干扰，而这一类对象暂态性能都较差，从而导致整个回路振荡.振荡产生的暂态误差难以通过计算预测得到，从而影响控制系统性能评估的准确性.

为避免控制器快速切换带来的暂态误差对控制性能评估的影响，本文提出以“判断-加权”的方式获取多模型混合广义最小方差控制器Qmixing，并将其作用下闭环回路的广义输出方差作为性能评估的基准.多模型混合广义最小方差控制器Qmixing的设计路线如图 2所示.

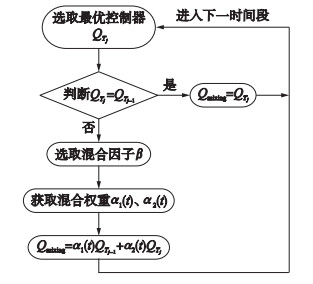
图 2 多模型混合广义最小方差控制器设计路线 Figure 2 Design framework of generalized minimum variance controller based on multiple model mixing method
图选项

控制器的选取   在Tj时间段，从QI中选取使定义的广义方差最小的控制器作为该时间段最优控制器QTj(z-1).

判断   判断选取的控制器QTj(z-1)与上一时间段选取的控制器QTj-1(z-1)是否相同.若相同，则：

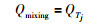
(16)

多模型混合策略   若QTj(z-1)与QTj-1(z-1)不同，则Qmixing通过如下方式得到：

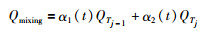
(17)

式中，α1(t)、α2(t)分别为QTj-1(z-1)与QTj(z-1)的混合权重且满足：

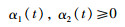
(18)
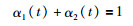
(19)
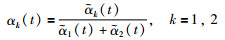
(20)

(t)为未规范化权重因子，必须满足连续可微条件.当时，本文取：

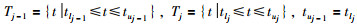
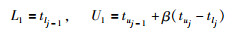
(21)
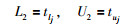
(22)
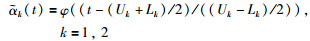
(23)
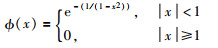
(24)

其中，β为混合因子，可根据Tj的范围进行调整.

多模型混合广义最小方差控制器Qmixing确定后，本文采取性能指标：

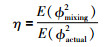
(25)

其中，E(ϕmixing2)为多模型混合广义最小方差控制器Qmixing作用下的广义方差，E(ϕactual2)为实际控制器Qactual作用下回路的广义方差.通过比值η即可对闭环回路控制性能具有的提升潜能进行评估.

4 乙烯裂解炉仿真研究

乙烯裂解炉是化工领域内最重要的装置之一，其控制性能的好坏，对整个乙烯工业过程的平稳运行、能耗物耗及最后总的经济效益有着极为重要的影响.乙烯裂解炉的双烯收率(乙烯、丙烯收率之和)与汽烃比、裂解炉平均出口温度、进料量、油品属性等因素有关.在本次仿真中，取乙烯裂解炉在多个扰动下的CARMA(controlled auto-regressive moving average)模型为

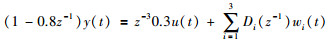
(26)
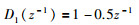
(27)
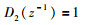
(28)
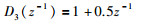
(29)

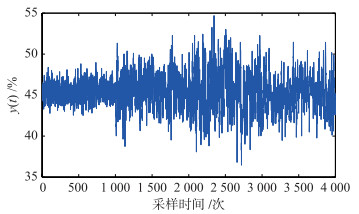
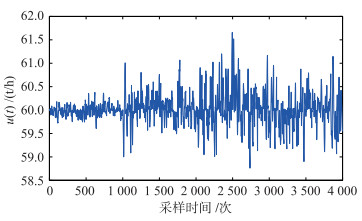
其中，y(t)为乙烯裂解炉出口处的双烯收率，u(t)为乙烯裂解炉入口处的进料量，D1(z-1)、D2(z-1)、D3(z-1)分别为乙烯裂解炉平均出口温度、汽烃比、油品属性的扰动传递函数.此外，D1(z-1)、D2(z-1)、D3(z-1)的扰动作用时间分别为0~3 000采样时间、1 000~3 000采样时间、2 000~4 000采样时间.因此，整个过程划分为4个时间段，分别为T1：0~1 000采样时间段、T2：1 001~2 000采样时间段、T3：2 001~3 000采样时间段与T4：3 001~4 000采样时间段.当闭环回路在式(30)所示的实际控制器作用下时，乙烯裂解炉的输出与实际控制器的输出如图 3、4所示：

图 3 多个扰动下的乙烯裂解炉输出 Figure 3 Output of ethylene cracking furnace with multiple disturbances
图选项
图 4 多个扰动下的实际控制器输出 Figure 4 Output of actual controller with multiple disturbances
图选项
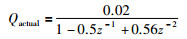
(30)

现采用本文提出的基于多模型混合的广义最小方差控制性能评估方法，对式(30)所示控制器作用下的乙烯裂解炉控制系统进行性能评估，取：

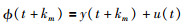
(31)

并基于D1(z-1)、D2(z-1)、D3(z-1)设计广义最小方差控制器Q1(z-1)、Q2(z-1)、Q3(z-1)以获得控制器集QI 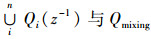与Qmixing.分别取β=0.2与β=0.6，在多模型混合广义最小方差控制器Qmixing(β=0.2)与Qmixing(β=0.6)作用下的广义输出方差与以广义输出方差为基准的性能指标分别如表 1、2所示.

表 1 不同控制器作用下的广义输出方差 Table 1 Generalized variance based on different benchmark controller
采样时间/次 0~1 000 1 001~2 000 2 001~3 000 3 001~4 000 0~4 000
Q1(z-1) 1.072 7 3.448 7 6.878 8 3.719 8 3.806 2
Q2(z-1) 1.229 8 3.434 0 6.580 8 3.368 0 3.668 8
Q3(z-1) 1.749 9 4.003 9 7.067 5 3.331 2 4.050 8
Qswitch(z-1) 1.072 7 3.434 0 6.580 8 3.331 2 3.619 4
Qmixing(z-1)(β=0.2) 1.072 7 3.458 1 6.673 4 3.331 2 3.648 3
Qmixing(z-1)(β=0.6) 1.072 7 3.446 1 6.701 3 3.331 2 3.652 9
Qactual(z-1) 1.094 1 3.849 9 8.009 5 4.379 6 4.356 2
表选项
表 2 基于不同控制器的性能指标 Table 2 Performance index based on different benchmark controller
采样时间/次 0~1 000 1 001~2 000 2 001~3 000 3 001~4 000 0~4 000
Q1(z-1) 0.980 4 0.895 8 0.858 8 0.849 3 0.873 7
Q2(z-1) 1.124 0 0.892 0 0.821 6 0.769 0 0.842 2
Q3(z-1) 1.599 4 1.040 0 0.882 4 0.760 6 0.929 9
Qswitch(z-1) 0.980 4 0.892 0 0.821 6 0.760 6 0.830 9
Qmixing(z-1)(β=0.2) 0.980 4 0.898 2 0.833 2 0.760 6 0.837 5
Qmixing(z-1)(β=0.6) 0.980 4 0.895 1 0.836 7 0.760 6 0.838 6
表选项

表 1中的行表示每一时间段在相应控制器作用下按式(31)定义的广义输出方差. 表 2中的行表示以相应广义输出方差为基准，按式(25)计算得到的性能指标.

从表 1中看到，Qmixing(z-1)(β=0.2/0.6)不仅在0~4 000整个过程的广义输出方差比Q1(z-1)、Q2(z-1)、Q3(z-1)作用下的广义输出方差小，而且在表 2中，基于Qmixing(z-1)(β=0.2/0.6)的广义输出方差性能指标在各个时间段都不会大于1，而基于Q2(z-1)、Q3(z-1)的广义输出方差性能指标分别在0~1 000采样时间、0~1 000采样时间与1 001~2 000采样时间大于1.若性能指标大于1，则表明作为基准的广义输出方差比实际控制器作用下的广义输出方差更大，无法评估当前实际控制器具有的提升潜能而失去作为基准的意义.因此，本文提出的控制器Qmixing(z-1)比Q1(z-1)、Q2(z-1)、Q3(z-1)单独作用下更能作为基准评估乙烯裂解炉控制系统的性能.

在每一时间段，从Q1(z-1)、Q2(z-1)、 Q3(z-1)中选取最小的广义输出方差作为Qswitch(z-1)控制器作用下闭环回路的理想广义输出方差，并计算相应的性能指标.从表 1与表 2中看到，在各个时间段，Qmixing(z-1)(β=0.2/0.6)与Qswitch(z-1)的广义输出方差、性能指标都基本一致.然而，在实际应用中，如PID系统中，控制器切换会导致系统振荡，甚至系统不稳定，而系统振荡产生的误差在Qswitch(z-1)性能指标计算中难以加以考虑，因此，实际过程中的Qswitch(z-1)并不能达到表 2中的性能指标. 表 2分别给出了β=0.2与β=0.6时的Qmixing(z-1)性能指标.当β=0.2时，Qmixing(z-1)在0~4 000整个过程的性能指标更接近Qswitch(z-1)的性能指标.当设计Qmixing(z-1)控制器时，β越趋于0，Qmixing(z-1)的混合时间越短而使Qmixing(z-1)越趋于Qswitch(z-1).当β取值过小时，Qmixing(z-1)也会导致系统振荡，致使根据扰动数据计算得到的基准与实际过程不符而失去意义.因此，β应根据实际过程进行取值.本文提出的Qmixing(z-1)以“判断—加权”的方式解决了控制器快速切换存在的暂态误差问题，根据其计算出来的基准更符合实际乙烯裂解炉生产而更有效.

5 结论

本文提出的基于多模型混合的广义最小方差性能评估方法综合考虑了控制器输出方差与被控对象输出方差对控制器的设计的影响，提出了一种“判断—加权”的控制策略，能有效地对多个扰动的控制系统进行性能评估；与常规的基于单个扰动的性能评估方法相比，能有效考虑所有扰动特性对性能评估的影响；与常规的基于切换的性能评估方法相比，两者评估有效性基本一致，却能有效解决控制器切换带来的暂态误差问题，而更具有实际应用价值.

参考文献
[1] Harris T. Assessment of closed loop performance[J]. Canadian Journal of Chemical Engineering , 1989, 67 (5) : 856–861. DOI:10.1002/cjce.v67:5
[2] Huang B, Shah S L. Perfomanceassessment ofcontrol loops:Theory and application[M]. Berlin, Germany: Springer , 1999 : 9 -106.
[3] Rubens H. Design of digital controllers for randomly disturbed systems[J]. Proceedings of the Institution ofElectrical Engineers , 1971, 118 (10) : 1503–1506. DOI:10.1049/piee.1971.0275
[4] Grimble M J. Controller performance benchmarking and tuning using generalised minimum variance control[J]. Automatica , 2002, 38 (12) : 2111–2119. DOI:10.1016/S0005-1098(02)00141-3
[5] Grimble M J. Non-linear generalized minimum variance feedback, feedforward andtracking control[J]. Automatica , 2005, 41 (6) : 957–969. DOI:10.1016/j.automatica.2004.12.009
[6] Guo J, Du W, Qian F. Performance bound of parallel cascade control system based on minimum variance and generalized minimum variance benchmarking[C]//10th World Congress on Intelligent Control and Automation. Piscataway, NJ, USA:IEEE, 2012:1334-1339.
[7] Patete A, Furuta K, Tomizuka M. Self-tuning control based on generalized minimum variance criterion forauto-regressive models[J]. Automatica , 2008, 44 (8) : 1970–1975. DOI:10.1016/j.automatica.2007.11.008
[8] Ando K, Masuda S. A direct control parameter tuning method using generalized minimum variance evaluation[C]//2014 International Conference on Advanced Mechatronic Systems. Piscataway, NJ, USA:IEEE, 2014:99-104.
[9] Zhao Y, Su H, Chu J, et al. Multivariable control performance assessment based on generalized minimum variance benchmark[C]//Proceedings of the IEEE Conference on Decision and Control. Piscataway, NJ, USA:IEEE, 2009:1902-1907.
[10] Olaleye F, Huang B, Tamayo E. Performance assessment of control loops with time-variant disturbance dynamics[J]. Journal of Process Control , 2004, 14 (8) : 867–877. DOI:10.1016/j.jprocont.2004.02.003
[11] Xu F, Lee K H, Huang B. Monitoring control performance via structured closed loop response subject to output variance/covariance upper bound[J]. Journal of Process Control , 2006, 16 (9) : 971–984. DOI:10.1016/j.jprocont.2006.05.003
[12] Zhou M, Xie L, Pan H, et al. Performance assessment of PID controller with time-variant disturbance dynamics[C]//Proceedings of International Symposium on Advanced Control of Industrial Processes. Piscataway, NJ, USA:IEEE, 2011:650-655.
[13] Aufderheide B, Prasad V, Bequette B W. A comparison of fundamental model-based and multiple modelpredictive control[C]//Proceedings of the 40th IEEE Conference on Decision and Control. Piscataway, NJ, USA:IEEE, 2001:4863-4868.
[14] Mazinan A H, Sadati N. Fuzzy predictive control based multiple models strategy for a tubular heat exchanger system[J]. Applied Intelligence , 2010, 33 (3) : 247–263. DOI:10.1007/s10489-009-0163-1
[15] Ohnishi Y. A switching method of PID controllers based on performance assessment[C]//ICROS-SICE International Joint Conference. Piscataway, NJ, USA:IEEE, 2009:1907-1910.
[16] Ohnishi Y.Design of a switching nonlinear PID control system based on performance assessment[C]//Proceedings of SICE Annual Conference (SICE).Piscataway, NJ, USA:IEEE, 2011:2619-2623.
[17] Joao P H, Paolo S, Gregory S.Optimal controller initialization for switching between stabilizing controllers[C]//Proceedings of the 46th IEEE Conference on Decision and Control.Piscataway, NJ, USA:IEEE, 2007:5634-5639.
[18] Yame J J, Qiao H.Conditioned switching between two-degree-of-freedom controllers for plants with changing dynamics[C]//201011th International Conference on Control Automation Robotics &Vision.Piscataway, NJ, USA:IEEE, 2010:945-951.
[19] 张巍, 王昕, 王振雷. 基于多模型混合最小方差控制的时变扰动控制系统性能评估[J]. 自动化学报 , 2014, 40 (9) : 2037–2044. Zhang W, Wang X, Wang Z L. Performance assessment of control loop withtime-variant disturbance dynamics based on multi-model mixing minimum variance control[J]. ActaAutomaticaSinica , 2014, 40 (9) : 2037–2044.
[20] 刘春平, 王昕, 王振雷. 基于MMTMV方法的多变量时变扰动系统性能评估[J]. 自动化学报 , 2015, 41 (5) : 928–935. Liu CP, Wang X, Wang ZL. Performance assessment of MIMO system with time-variant disturbances based on MMTMV method[J]. Acta Automatica Sinica , 2015, 41 (5) : 928–935.
http://dx.doi.org/10.13976/j.cnki.xk.2016.0588
中国科学院主管，中国科学院沈阳自动化研究所、中国自动化学会共同主办。
0

文章信息

刘春平, 王昕, 王振雷
LIU Chunping, WANG Xin, WANG Zhenlei
基于多模型混合的广义最小方差控制性能评估
Performance Assessment of Control Systems Based on a Multiple-model Mixing Method with Generalization Minimum Variance
信息与控制, 2016, 45(5): 588-592, 599.
Information and Control, 2016, 45(5): 588-592, 599.
http://dx.doi.org/10.13976/j.cnki.xk.2016.0588

文章历史

收稿/录用/修回: 2015-09-24/2015-01-29/2016-03-17

工作空间