2. 长安大学电子与控制工程学院, 陕西 西安 710064
2. School of Electronic & Control Engineering, Chang'an University, Xi'an 710064, China
1 引言
目标跟踪是无线传感器网络的一个重要任务,但是由于能量、频率和带宽等物理资源的限制,并不是所有的传感器节点都能参与目标跟踪.传感器管理就是选择一组最优的传感器节点,在获得较好的跟踪性能的同时,又能降低网络能量、带宽等资源消耗[1-4].
后验克拉美—罗下界(PCRLB)是目标状态估计的Fisher信息矩阵(FIM)的逆矩阵,它给出了目标状态估计误差理论上的下界,文[5]提出基于PCRLB的传感器部署方法,实现传感器资源的有效利用,文[6]对这一方法进一步扩展,考虑了传感器部署和运动的不确定性.但是当前的传感器管理方法都是针对的集中式传感器网络,在这些网络中,只有一个中央融合中心对传感器节点进行管理,是一种集中式管理方法.
文[7]提出了条件PCRLB(CPCRLB),给出了目标状态估计的一步预测误差下界,适合于作为无线传感器网络资源管理的准则. Tharmarasa等[8]针对无线传感器网络目标跟踪问题,给出了PCRLB的一种近似的分布式算法. Mohammadi等[9]提出了一种最优的PCRLB的分布式算法且应用于传感器选择.文[10]针对分布式传感器网络,提出了一种分布式CPCRLB(DCPCRLB)算法.在分布式方法中,每个传感器节点只与自己的邻居传感器节点通讯,因而具有较低的带宽消耗和灵活的网络拓扑结构,对网络链接具有较强的鲁棒性.
2 预备知识和问题描述 2.1 分布式粒子滤波器考虑一个层次型无线传感器网络,该网络具有两种类型的传感器节点,局部融合节点和观测节点,观测节点只进行观测,局部融合节点负责对自己监视邻域内的观测节点进行管理,进行信息收集和融合处理,并且通过与其相连接的其它局部融合节点的通讯和协作,获得目标状态的全局估计.设传感器网络由Nf个局部融合节点和Ns个观测节点组成.目标状态变量x(k)是不可观的一阶马尔可夫过程,其离散时间动态方程为
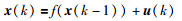
|
(1) |
其中,u(k)是独立同分布的(i.i.d)过程噪声.在分散式无线传感器网络中,设局部融合节点l在自己邻域内选择激活的观测节点集合为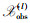
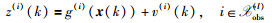
|
(2) |
其中,v(i)(k)是i.i.d的量测噪声.
文[11-12]对分布式无线传感器网络,基于一致性算法提出一种分布式粒子滤波器,其中每个局部融合节点l运行两个粒子滤波器,获得两组加权粒子集,第1个滤波器称为局部粒子滤波器,它只利用融合节点l获得的局部观测集合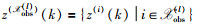
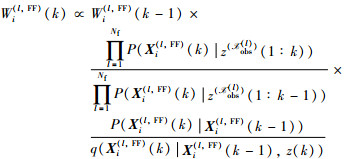
|
(3) |
在式(3)中,只有第1个分式要求所有的局部融合节点参与,为了计算式(3)中的乘积项,利用高斯分布逼近:
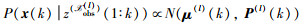
|
(4) |
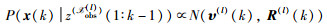
|
(5) |
其中,μ(l)(k)和P(l)(k)是k时刻局部融合节点l的局部滤波密度的均值和协方差,υ(l)(k)和R(l)(k)是k时刻局部预测密度的均值和协方差.利用来自局部粒子滤波器的局部粒子{Xi(l,LF)(k),Wi(l,LF)}得到:
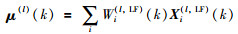
|
(6) |
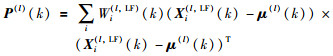
|
(7) |
利用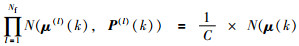
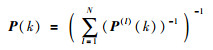
|
(8) |
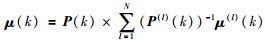
|
(9) |
同样地,式(3)中的局部预测分布的乘积项也可以逼近为高斯分布N
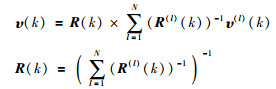
|
(10) |
对于上述乘积分布中的参数μ(k)、p(k)和υ(k),R(k)可以用平均一致性算法来实现[10]:
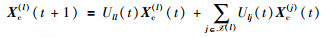
|
(11) |
其中,Xc(l)(t)是在融合节点l处的一致性变量,t是一致性迭代变量,
CPCRLB给出了在已知过去所有量测值z(1:k)的条件下,当获得新的量测z(k+1)时,估计目标状态x(k+1)的均方误差(MSE)下界,即:
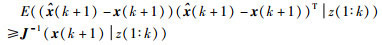
|
(12) |
其中,E代表数学期望,J(x(k+1)z(1:k))表示目标状态估计值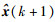
文[14]给出了一个直接的条件FIM近似迭代公式:
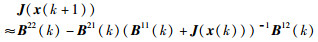
|
(13) |
其中,
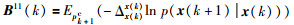
|
(14) |
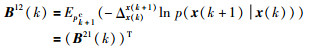
|
(15) |
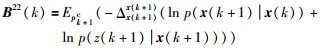
|
(16) |
其中,pk+1c=p(x(0:k+1),z(k+1)z(1:k)).式(13)给出了在已知网络所有量测下的全局条件Fisher信息矩阵,适用于带有中央融合中心的集中式网络结构.文[9-10]中给出了一种PCRLB的分布式算法,本文把该方法推广到条件FIM,基于平均一致性策略给出一种融合节点的全局条件FIM的分布式迭代算法:
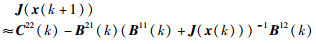
|
(17) |
其中,J(x(k+1))是融合节点对应于全局估计的全局条件FIM,C22(k)由式(18)给出:
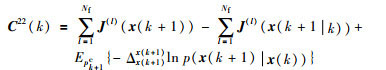
|
(18) |
其中,J(l)(x(k+1))是融合节点l基于局部观测信息z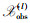
针对实际中的非线性目标跟踪问题,局部条件FIM和全局条件FIM通常没有解析解,本文将借助于局部粒子滤波器和融合粒子滤波器得到的加权粒子对全局条件FIM和局部条件FIM中的数学期望进行逼近[7, 15].
对式(18)中的求和项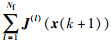
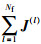
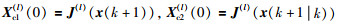
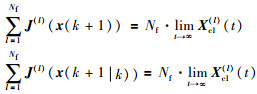
|
无线传感器网络下,设目标状态向量为x(k)=[ξ,η,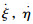
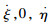
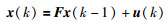
|
(19) |
其中,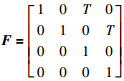
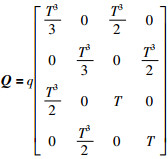
传感器节点测量模型为一个信号强度衰减模型,传感器节点n接受到的目标信号强度(RSS)量测为
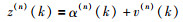
|
(20) |
其中,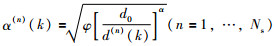
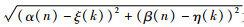
对目标运动模型(19)和量测模型(20),计算DCPCRLB的全局条件FIM和局部条件FIM所需的数学期望为
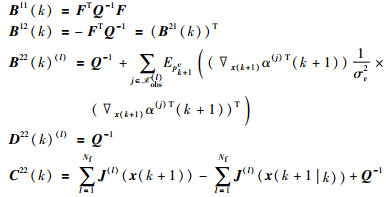
|
对于局部FIM J(l)(x(k+1))中的数学期望项B22(k)(l),类似于文[15],借助于局部融合节点获得的局部粒子{Xi(l,LF)(k),Wi(l,LF)}对其进行蒙特卡洛逼近.
3.2 分散式传感器管理层次型网络由若干个局部融合节点和大量的观测节点构成,层次型网络结构与传统的集中式网络结构不同,不存在一个唯一的中央融合中心,而是包含许多个局部融合节点.每个局部融合节点负责一小块监视区域,并对该区域内的观测节点进行管理.观测节点具有有限的能量,只负责对感知区域内的目标信息进行观测,并将观测信息传递给相应的局部融合节点.每个局部融合节点在自己的监视区域内选择并激活观测节点,收集自己邻域内观测节点的信息.每个局部融合节点只与自己相邻的局部融合节点之间进行数据交换,并执行分布式估计.
在本文中,在各融合节点之间,采用分布式粒子滤波器和DCPCRLB,是一种完全的分布式处理.对融合节点管理的小区域内部的观测节点,采用集中式处理方法.相对于集中式传感器管理,该方法称为分散式或者集散式管理.
由于网络物理资源的限制,每个局部融合节点在每个时刻只能选择有限个观测节点,设融合节点l能够利用的最大观测节点个数为Ml,并且网络中激活的观测节点的总数也是受到限制的.将目标状态估计的CPCRLB作为传感器节点选择的准则,在k+1时刻,局部融合节点选择观测节点的全局代价函数为
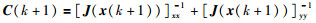
|
(21) |
其中[J(x(k+1))]xx和[J(x(k+1))]yy是全局条件FIM对应于目标x坐标和y坐标的分量,即代价函数为目标位置坐标分量的全局CPCRLB边界之和,每个局部融合节点选择观测节点子集应当使得全局代价函数(21)最小.
全局条件FIM与网络中所有局部融合节点的局部条件FIM有关,但是每个局部融合节点不具有网络全局知识,为了获得最优的全局性能,每个局部融合节点在选择自己的观测节点时,也要考虑其他局部融合节点的观测节点的选择,最优观测节点的选择需要局部融合节点之间的协作.
式(21)的最优解是一个NP难组合优化问题,其计算复杂度随观测节点个数是指数增加的,对大规模无线传感器网络,完整的穷举是不可行的.直观地,观测节点的性能越好,被选中的机会越大,采用下面的融合节点—观测节点对(l,ml)的局部代价函数度量局部观测节点的性能:
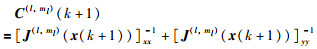
|
(22) |
其中,J(l,ml)(x(k+1))是k+1时刻局部融合节点l选择观测节点ml时的局部条件FIM.
为了找到问题的次优解,本文基于一致性策略提出一种迭代的局部搜索算法,具体的算法步骤如下:
算法1迭代局部搜索算法.
Step 1选择一组初始可行解:
(1)对第1个局部融合节点,选择第1个观测节点,使得当只有一个观测节点时的全局代价函数最优.
(2)对第2个局部融合节点,选择一个观测节点,使得当前选择的传感器节点对应的全局代价函数最优.
(3)继续为后续每一个局部融合节点选择第1个观测节点.
(4)重复以上过程,为每个局部融合节点选择第2个观测节点,直到每个局部融合节点最大个数的观测节点被选中.
在上述每一步中,使用了穷举搜索方法来决定哪个观测节点应该被选择,当计算全局代价函数时,采用了前面提到的基于平均一致性的分布式CPCRLB算法,利用了局部融合节点之间的信息交换.由于局部融合节点管理的观测节点个数是有限的,所以穷举法在计算上是可行的.
Step 2在初始解的邻域内搜索更好的解.
(1)对每个融合节点l,每次去掉一个选中的节点,用另一个节点替换,然后利用基于平均一致性的分布式算法计算全局条件FIM,如果新的节点组合获得更好的全局代价函数性能,则接受该组节点,直到所有的观测节点被穷举.
(2)每次交换两个观测节点,用同样的方法寻找更好的解.
(3)继续增加交换的观测节点个数,直到所有的观测节点被穷举或者到达指定的迭代次数限制.
在局部搜索过程中,对每个局部融合节点,按照观测节点的局部代价函数式(22)的次序依次交换观测节点,能够很快找到每种交换结构邻域内的局部最优解[8].以上局部搜索算法的计算复杂度为O(NfNlMl),其中Nf为融合节点的个数,Nl为融合节点l的所有观测节点的个数,Ml为选中的节点个数.
设局部融合节点l选择的观测节点集合为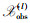
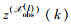
算法2分散式传感器观测节点选择.
Step 1对每对融合节点l和其邻域内的观测节点ml,计算局部代价函数C(l,ml)(k+1).
Step 2利用算法1给出的迭代局部搜索算法,首先为每个局部融合节点选择一组初始观测节点,然后利用交换方法,通过局部搜索,最终每个局部融合节点l在自己的监视邻域内选择一组次优的观测节点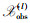
Step 3每个融合节点l激活观测节点子集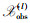
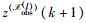
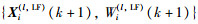
Step 4局部融合节点l执行一致性融合粒子滤波器:将计算融合粒子滤波器权值所需的乘积项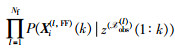
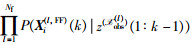
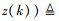
Step 5基于平均一致性算法用分布式方法计算全局条件FIM J(x(k+1)),并且从融合粒子滤波器得到目标状态的全局估计.
4 仿真结果设无线传感器网络由153个节点构成,包含Nf=9个局部融合节点和Ns=144个观测节点,部署在一个240 m×240 m的正方形区域内.为简单起见,假定每个局部融合节点的监视邻域为一个80 m×80 m的矩形区域,观测节点均匀分布在该区域内,融合节点位于该矩形的中心.融合节点可以与自己监视邻域内的观测节点之间通讯,并且可以与通信半径是100 m的其他局部融合节点通信.假设每个融合节点的监视邻域之间没有重叠,并且每个局部融合节点至少与网络内的另一个局部融合节点相连.由于带宽的限制,设每个观测时刻,每个局部融合节点最多选择Ml=2个观测节点,网络激活的最大观测传感器节点个数为Nmax=18.
在RSS观测模型(25)中,目标信号衰减指数α=2,目标辐射的信号能量在d0=1 m处φ=1 000.假定所有传感器节点的量测噪声具有相同的方差σv2=0.1.目标运动过程噪声参数q=1,采样周期T=1 s,仿真时间为20 s.目标状态先验分布为高斯分布,均值为x(0)=[30, 30, 10, 10]T,协方差矩阵为diag{20,20,5,5}.采用一致性分布式粒子滤波器,每个融合节点的局部粒子滤波器和全局融合粒子滤波器的粒子个数都取为1 000.
将本文提出的基于DCPCRLB的分散式传感器选择方法与另外两种分散式传感器选择方法进行比较:
(1)随机传感器选择方法(random):每个融合节点在它的矩形监视邻域内随机选择传感器观测节点.
(2)最近邻传感器选择方法(closest):如果目标的预测位置在某个融合节点的矩形邻域内,该融合节点选择距离目标预测位置最近的观测节点,其它局部融合节点的观测节点随机选取.
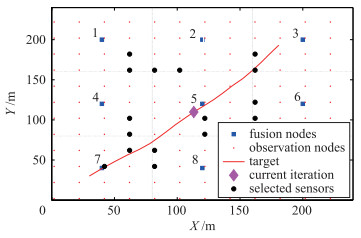
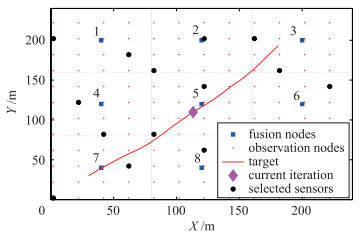
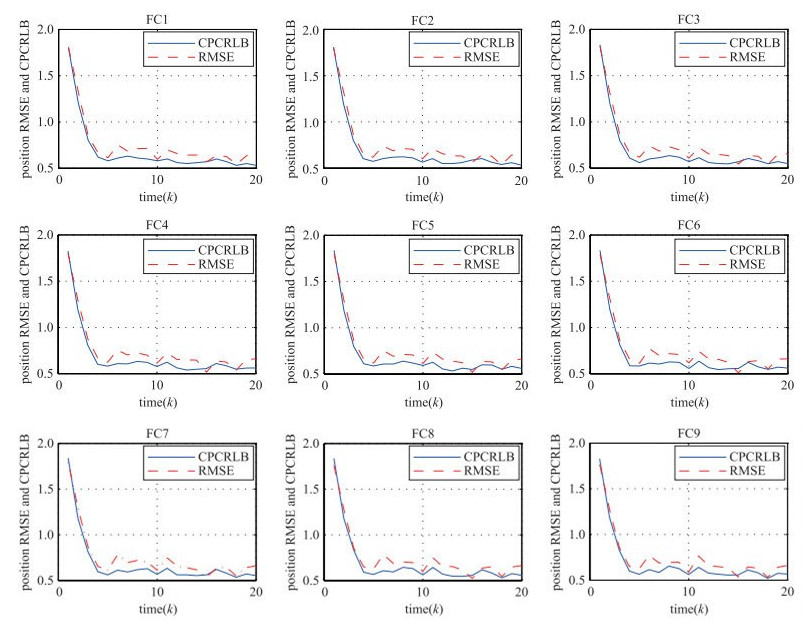
图 1~图 3分别给出了当仿真时刻k=11时基于本文的DCPCRLB传感器选择方法及最近邻方法和随机方法选择的观测节点集合,其中矩形表示局部融合节点,小圆圈代表观测节点,大圆圈表示选中的观测节点,菱形表示当前时刻的目标位置.采用DCPCRLB传感器选择方法,利用一致性分布式粒子滤波器对目标进行跟踪,基于100次蒙特卡洛仿真的平均结果,图 4给出了每个局部融合节点的融合粒子滤波器对目标位置估计的全局均方根误差(RMSE)及目标位置估计的全局CPCRLB的平方根.从图中可以看到每个局部融合中心得到的目标位置估计的RMSE与其相应的CPCRLB非常接近.而且每个局部融合中心的RMSE曲线几乎相同,CPCRLB曲线也几乎相同,说明经过分布式一致性融合后,所有局部融合节点目标状态全局估计值达到了近似平均一致,CPCRLB的全局估计值也达到了近似平均一致,其中轻微的差异是由于一致性算法的有限次迭代带来的不充分收敛导致的. 图 4中部分RMSE曲线低于CPCRLB是由于粒子滤波器采样算法的随机性引起的.
|
| 图 1 k=11时刻基于DCPCRLB方法选择的传感器 Figure 1 Selected sensors based on DCPCRLB when k=11 |

|
| 图 2 k=11时刻基于最近邻方法选择的传感器 Figure 2 Selected sensors based on closest neighbor when k=11 |
|
| 图 3 k=11时刻基于随机方法选择的传感器 Figure 3 Selected sensors based on random method when k=11 |
|
| 图 4 局部融合节点目标位置估计的全局RMSE和CPCRLB Figure 4 Global EMSE and CPCRLB of target position when local fusion nodes |
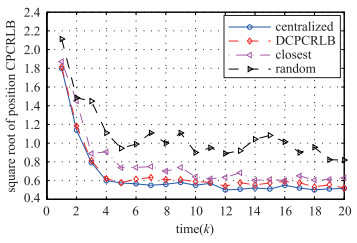
局部融合节点利用以上3种分散式传感器选择算法所选择的传感器节点获得目标位置估计的全局CPCRLB,通过对所有融合节点的全局CPCRLB取平均值,图 5分别给出了3种传感器选择算法得到的目标位置估计的全局CPCRLB的均方根.从中可以看到基于DCPCRLB的传感器选择算法所得到的传感器节点集合给出了最低的误差边界,图 5中也给出了所有传感器节点都参与时的集中式最优CPCRLB(centralized).仿真结果表明尽管DCPCRLB方法只选择了有限个传感器节点,但基于DCPCRLB方法得到的CPCRLB与基于所有传感器节点参与的集中式方法所得到的CPCRLB非常接近.
|
| 图 5 3种分散式传感器选择方法的全局CPCRLB和集中式CPCRLB Figure 5 CPCRLB of the three proposed decentralized sensor selection methods and centralized CPCRLB |
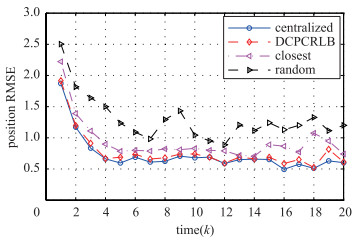
基于3种分散式传感器选择方法,采用一致性分布式粒子滤波器,通过对所有局部融合节点融合粒子滤波器的滤波结果取平均值,图 6给出了全局目标位置估计的RMSE,图中也给出了所有传感器节点都参与时集中式粒子滤波器对目标位置估计的RMSE(centralized).从图 6中可以看出DCPCRLB方法误差最小,最近邻方法次之,并且DCPCRLB方法跟踪精度非常接近于当所有的传感器节点都参与时的集中式粒子滤波器的跟踪精度.尽管最近邻和随机传感器选择方法的计算复杂性远低于DCPCRLB方法,但是DCPCRLB方法对目标位置估计的RMSE性能比最近邻方法好34%,比随机方法好41%.而且仿真结果也表明基于DCPCRLB的传感器选择方法尽管只选择了有限个传感器节点,但是实现了与集中式滤波器非常接近的目标跟踪精度.
|
| 图 6 3种分散式传感器选择方法的RMSE和集中式RMSE Figure 6 RMSE of the three proposed decentralized sensor selection methods and RMSE of centralized method |
本文对无线传感器网络下目标跟踪的传感器节点管理问题,基于分布式CPCRLB提出一种分散式传感器选择策略.基于一致性算法给出了一种CPCRLB的分布式迭代算法,同时基于一致性分布式粒子滤波对CPCRLB进行数值逼近计算,最后基于平均一致性算法给出了一种分散式传感器管理的局部搜索算法.在后续的研究中,将把该方法推广到传感器网络下多目标跟踪的分散式传感器节点管理.
| [1] | Kumar S, Zhao F, Shepherd D, et al. Special issue on collaborative signal and information processing in microsensor networks[J]. IEEE Signal Processing Magazine , 2002, 19 (2) : 1–14. |
| [2] | 刘欣怡, 赵诚, 单甘霖, 等. 面向目标跟踪的基于Rényi信息增量多的传感器管理[J]. 信息与控制 , 2015, 44 (2) : 184–189. Liu X Y, Zhao C, Shan G L, et al. Multi-sensor management based on Rényi information gain for maneuvering target-tracking[J]. Information and Control , 2015, 44 (2) : 184–189. |
| [3] | 肖金超, 曾鹏, 何杰, 等. 基于传感器网络的多信道定位技术[J]. 信息与控制 , 2015, 44 (3) : 346–352. Xiao J C, Zeng P, He J, et al. Multi-channel localization technology based on sensor networks[J]. Information and Control , 2015, 44 (3) : 346–352. |
| [4] | 罗开平, 姜维, 李一军. 传感器管理述评[J]. 电子学报 , 2010, 38 (8) : 1900–1907. Luo K P, Jiang W, Li Y J. Review of sensor management[J]. Acta Electronica Sinica , 2010, 38 (8) : 1900–1907. |
| [5] | Hernandez M L, Kirubarajan T, Bar-Shalom Y. Multisensor resource deployment in the presence of clutter using Cramer-Rao lower bounds[J]. IEEE Transaction on Aerospace and Electronic Systems , 2004, 40 (2) : 399–416. DOI:10.1109/TAES.2004.1309993 |
| [6] | Punithakumar K, Kirubarajan T, Hernandez M L. Multisensor deployment using PCRLBs, incorporating sensor deployment and motion uncertainties[J]. IEEE Transaction on Aerospace and Electronic Systems , 2006, 42 (4) : 1474–1485. DOI:10.1109/TAES.2006.314587 |
| [7] | Zuo L, Niu R, Varshney P K. Conditional posterior Cramer-Rao lower bounds for nonlinear sequential Bayesian estimation[J]. IEEE Transaction on Signal Processing , 2011, 59 (1) : 1–14. DOI:10.1109/TSP.2010.2080268 |
| [8] | Tharmarasa R, Kirubarajan T, Sinha A, et al. Decentralized sensor selection for large-scale multisensor-multitarget tracking[J]. IEEE Transaction on Aerospace and Electronic Systems , 2011, 47 (2) : 1307–1324. DOI:10.1109/TAES.2011.5751260 |
| [9] | Mohammadi A, Asif A. Distributed posterior Cramer-Rao lower bound for nonlinear sequential bayesian estimation[C]//IEEE 7th Sensor Array and Multichannel Signal Processing Workshop(SAM). Piscataway, NJ, USA:IEEE, 2012:509-512. |
| [10] | Mohammadi A, Asif A. Decentralized conditional posterior Cramér-Rao lower bound for nonlinear distributed estimation[J]. IEEE Signal Processing Letters , 2013, 20 (2) : 165–168. DOI:10.1109/LSP.2012.2235430 |
| [11] | Mohammadi A, Asif A. A consensus/fusion based distributed implementation of the particle filter[C]//Proceedings of the 4th IEEE International Workshop on Computational Advances in Multi-sensor Adaptive Processing. Piscataway, NJ, USA:IEEE, 2011:285-288. |
| [12] | Mohammadi A, Asif A. Distributed particle filter implementation with intermittent/irregular consensus convergence[J]. IEEE Transactions on Signal Processing , 2013, 61 (10) : 2572–2587. DOI:10.1109/TSP.2013.2245123 |
| [13] | Xiao L, Boyd S, Lall S. A scheme for robust distributed sensor fusion based on average consensus[C]//Proceedings of the ACM/IEEE International Conference on Information Processing in Sensor Networks. Piscataway, NJ, USA:IEEE, 2005:63-70. |
| [14] | Zheng Y, Ozdemir O, Niu R, et al. New conditional posterior Cramér-Rao lower bounds for nonlinear sequential Bayesian estimation[J]. IEEE Transactions on Signal Processing , 2012, 60 (10) : 5549–5556. DOI:10.1109/TSP.2012.2205686 |
| [15] | 杨小军. 基于性能边界和量化数据的WSN目标跟踪传感器选择算法[J]. 电子学报 , 2014, 42 (6) : 1081–1085. Yang X J. Sensor selection for target tracking in wireless sensor networks based on performance bounds and quantized data[J]. Chinese Journal of Electronics , 2014, 42 (6) : 1081–1085. |



