2. 浙江中控系统工程有限公司, 浙江 杭州 310052
2. Zhejiang Supcon Limited Company, Hangzhou 310052, China
1 引言
塔式太阳能热发电技术是利用多个跟踪太阳的定日镜,将太阳光聚集到接收器上,使光能转换为热能,加热管道中的介质,产生高温蒸汽从而使汽轮机发电[1].由于太阳能具有间歇性和不稳定性[2],会使聚集到接收器上的能量变动幅度较大,从而影响接收器的压力等性能及发电的稳定性,因此镜场调度,即通过调整定日镜聚焦情况使聚光能量满足系统需求,具有十分重要的意义.
目前,镜场调度问题已经有许多学者做了相关研究.在镜场调度目标上,文[3-5]都是将投射到接收器上的光能量最大化作为目标函数;文[6]的调度目标是最大限度地减少镜场的总能量消耗;文[7]的调度目标为接收器表面能流峰值最小;文[8-9]的调度目标为接收器表面能量分布均匀.但是,这些研究都没有考虑系统的实际能量需求.在调度实现策略上,文[10]创新性地对接收器建立了过热评价模型并根据接收器是否过热来对接收器的聚焦点进行调整,减小局部过热,但在调度策略上仅按照经验排序调度,不适用于大规模镜场调度.文[5]优化每面定日镜的聚焦点,这样虽然能够很精确地达到优化目标,但镜场运转操作成本会很大.文[11]以控制镜场能量输出稳定为目标,提出了基于误差修正的镜场调度问题,采用了区间调度的策略,减少了操作成本,但给了镜场输出能量一个裕度,使之不能精确满足需求值.
针对上述问题,本文提出一种新的基于整数规划的调度模型,以满足系统的能量需求为调度目标,使镜场可以在DNI(太阳直接辐照度)变化下输出系统所需的能量;优化策略上采取镜场分区策略,并采用贪婪—粒子群优化算法对其进行求解,保证计算的实时性,适合大规模镜场调度.通过模拟镜场实时调度及水—蒸汽接收器的压力控制这两个应用场景对方法的有效性进行了验证.本文以平板式接收器为例说明,也可以推广到其它形式的接收器,如柱状接收器等.
2 基于整数规划的镜场能量调度方法 2.1 调度模型由于一个镜场的镜子数往往有上万面,所以求解优化调度问题往往速度缓慢.为了解决这个问题,本文将全镜场分成两个区域,区域1中的定日镜数量占整个镜场的大部分,此区域镜子的聚焦状态在调度时不做调整,仅对其中区域2的镜场进行调度,从而减少决策变量数目,提高求解速度.本文称镜场1区为固定区,镜场2区为调度区.这也符合实际电站的操作成本要求.固定区提供基本的能量值为Qb,其值比每次调度需要满足的太阳能辐射值低(由此可以大致估算固定区中定日镜数量),同时由于太阳位置移动或天气改变,Qb会随着时间而变.如果系统所需的能量值为Qn,那么调度区镜场调度所需的能量值Qp为

|
(1) |
镜场调度需要围绕2个准则设计,分别为:
(1)满足能量需求;
(2)变动的镜子数少,节约操作成本.
调度模型目标函数如式(2)所示,约束函数如式(3)所示:
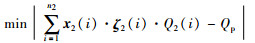
|
(2) |
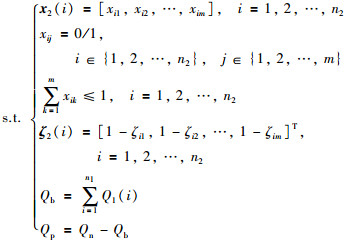
|
(3) |
其中,i表示镜子的序号;j表示聚焦点的序号;m表示聚焦点的个数;n1、n2分别为固定区和调度区的定日镜数量;决策变量x2(i)表示调度区第i面定日镜的状态,为m维0-1向量;分量xij表示第i面镜子是否照射到聚焦点j.由于一面镜子同时只能有一个聚焦点,因此向量x2(i)的和不大于1,全零向量表示不照射在接收器上,当某个分量xij为1时表示第i面镜子照射到聚焦点j,即决策变量要满足聚焦点选择约束;ζ2(i)为调度区第i面定日镜的溢出效率,为m维变量,分量ζij表示第i面镜子照射到聚焦点j时的溢出效率;Q1(i)和Q2(i)分别表示固定区和调度区第i面定日镜无溢出的能量值.调度的目标为使镜场调度区照射到接收器上的定日镜携带总能量尽可能接近所需能量Qp.
每面镜子的能量通过在镜面上随机撒点,根据蒙特卡洛光线追踪法计算每根光线投射到接收器中心上的能量得到:

|
(4) |
其中,Sh为每面镜子的面积,t为当前时刻,DNI为太阳光垂直入射强度,ηop为不考虑溢出的光学效率,具体计算公式为
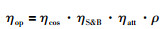
|
(5) |
其中,ηcos、ηS & B、ηatt、ρ分别为余弦效率、阴影遮挡效率、大气透射率和镜面反射率.
当定日镜照射到接收器上时,由于接收器上的聚焦点不同会导致每面定日镜的溢出效率不同,因此在调度模型中考虑了镜子的聚焦点选择.假设接收器面板上有m个聚焦点,如图 1所示.当定日镜i聚焦到聚焦点j,如果溢出率为ζij,那么每面镜子聚焦到接收器上的能量为(1-ζij)Q(i).溢出效率的计算参考文[12].具体聚焦点的选择在优化算法中说明.

|
| 图 1 接收器多聚焦点示意图 Figure 1 Schematic diagram of multiple focus on the receiver |
上述调度模型为非线性整数规划问题,为了兼顾求解精度和速度,本文将贪婪算法和粒子群优化算法相结合进行求解.贪婪算法的基本思想是将问题的求解过程看作是一系列的选择,每次选择都是当前状态下的最好选择(局部最优解)[13].贪婪算法的优点是求解快速,但求解不精.粒子群优化算法简单来说就是一群粒子在解空间中不停迭代更新自己的速度和位置以达到最优解的过程[14].粒子群优化算法能够在这类基于模型仿真的优化问题上快速优化得到近似全局最优解;同时相比于基于空间划分算法的搜索算法,粒子群优化算法能够更好地解决多决策变量的优化问题;而相比于遗传算法,粒子群优化算法对高维问题的收敛速度更快且优化结果很精确[16].
具体算法步骤为:
(1)将调度区的n2面镜子的能量从大到小排列为Qs[n2];
(2)从Qs[n2]中从前到后选择na面镜子满足需求能量Qp的ξ%(ξ可取70~80);
(3)利用粒子群优化算法在其余的n2-na面镜子中选择适当的镜子数,使其满足(1-ξ%)Qp.
其中,步骤(1)和步骤(2)体现了贪婪算法的思想,快速地缩小求解的范围,步骤(2)计算前na面镜子的流程图如图 2所示,其中Qs(i)表示调度区第i面镜子携带的能量值.步骤(3)粒子群中每个粒子的位置表示为向量:

|

|
| 图 2 计算na及na面镜子输出能量算法流程图 Figure 2 Algorithm flow chart of calculation of na and the output energy of na mirrors |
即所有x2(i)的集合.粒子速度为相同维数的向量:

|
采用针对0-1规划问题的二进制粒子群优化算法[16],同时考虑到聚焦点约束,算法实现步骤如下:
(1)初始化.随机初始化种群中各粒子的位置和速度.
(2)评价种群.将种群中各粒子的当前位置和适应值存储在各粒子的最好位置(pbest)中,将所有pbest中适应值最优个体的位置和适应值储存于全局最优位置(gbest).
(3)更新粒子速度和位置.首先按照式(6)更新粒子的速度,对于第i面定日镜,按照[xi1,xi2,…,xim]的顺序,首先判断前面的粒子位置是否全为0,若全为0,则按照式(7)计算一个随机数S,按照式(8)判断粒子位置是否为1;否则,转入下一面镜子的速度位置更新:

|
(6) |

|
(7) |

|
(8) |
其中,w为惯性权因子,w较大,全局收敛能力强,局部收敛能力弱,一般取值0.8~1.2;c1和c2为取值为正的学习因子(加速因子);r1、r2和r3为0到1之间均匀分布的随机数;pij为当前各粒子的最好位置(pbest),gij为当前全局最优位置(gbest).
(4)更新pbest.将每个粒子当前适应值与其经历过的最好位置的适应值做比较.如果较好,则用当前适应值和位置更新pbest.
(5)更新gbest.比较当前所有的pbest和gbest的适应值,若pbest中适应值最优的粒子较gbest更优,更新gbest.
(6)判断算法是否结束.若满足停止条件(通常为预先设定的运算精度或最大迭代次数),搜索停止并输出结果;否则,返回至步骤(3).
在更新粒子速度与位置时保证了聚焦点选择的约束能够满足.
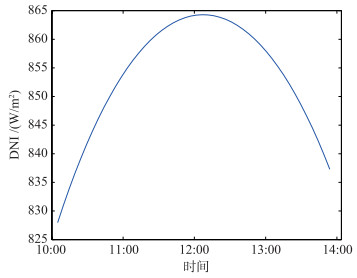
3 仿真研究 3.1 DNI变化时的镜场调度仿真本文利用上述方法针对一个模拟镜场进行了调度仿真,图 3为2013年7月23日杭州某地10:00-14:00的DNI曲线图,假设系统在此时间段的能量需求为305 kW.模拟镜场定日镜镜面面积为2 m2,镜面反射率取0.8,设镜场调度区镜子数量为100,聚焦点个数为5,ξ取70,调度周期为5 min.
|
| 图 3 DNI变化曲线 Figure 3 DNI change curve |
采用上述方法进行调度后镜场输出的能量值如图 4所示,其中虚线表示设定值,实线表示调度能量输出值.粒子群优化算法的参数通过多组参数实验然后凭经验选择效果较好的一组设置如下,粒子数目为200,c1和c2都取2,w为0.9,最大迭代次数为100.可以看出,经过能量优化调度,镜场能够较为精确地满足系统需求的能量值,但在某些时刻能量输出值与期望值之间仍存在偏差,这是由于虽然聚焦点不同可以提供不同的能量值,但定日镜数量有限,无法提供连续的能量值,不能保证输出的能量恰好等于期望值.考虑到实际中存在的不确定性,可以认为这个偏差在系统承受范围之内.

|
| 图 4 镜场调度输出能量值 Figure 4 Output energy of heliostat field scheduling |
图 5是对应的调度变动的镜子数,可以看出,在DNI不太充足的时刻,由于需要更多的镜子来提供能量,需要调动的镜子数偏多,而DNI充足的时刻,每面镜子携带的平均能量增多,需要调动的镜子数减少,这也符合镜场的调度规律.
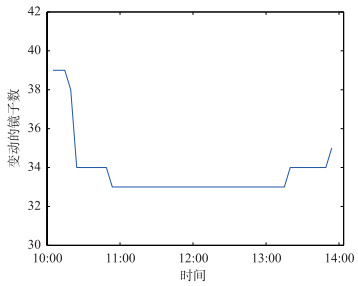
|
| 图 5 变动的镜子数目 Figure 5 The number of the changed mirrors |
水—蒸汽接收器的输入输出结构框图如图 6所示,系统输入变量为蒸汽流量、给水流量、接收器接收到的太阳辐射能;主要的输出变量是汽包液位值、系统压力.
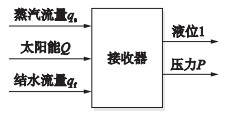
|
| 图 6 接收器输入输出示意图 Figure 6 Schematic diagram of the receiver inputs/outputs |
对于接收器控制系统来说蒸汽流量就相当于一个扰动,由于给水是直接影响液位的,所以给水流量控制液位,能量来控制系统压力.传统的水—蒸汽接收器控制通常采用PI控制[17-18],但没有考虑由于镜场能量离散性带来的执行结果与期望结果的偏差,为了使投射到接收器上的能量尽可能接近所需能量值,达到更好的控制效果,在控制过程中加入上文描述的镜场调度方法.
基于镜场调度的压力控制框图如图 7所示,其中,控制算法采用传统的PID控制算法,当压力值与设定值有偏差时,PID控制器计算出一个使压力回归到设定值的能量值,这个期望能量值就是镜场调度模块的目标值,通过上述方法进行镜场调度使镜场能量输出尽可能接近这个目标值,接收器产生压力反馈与设定值相比较,如此反复作用,使压力稳定在设定值附近.镜场调度模块相当于控制系统的执行机构,而这个执行机构的执行结果与期望结果可能会存在图 4所示的偏差.
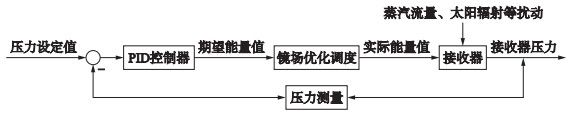
|
| 图 7 基于镜场调度的压力控制框图 Figure 7 Block diagram of the pressure control based on the heliostat field scheduling |
本节仿真对象是根据如下方程建立的水—蒸汽接收器模型:

|
(9) |

|
(10) |
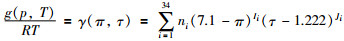
|
(11) |
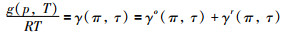
|
(12) |
式中,qf为给水流量,qs为蒸汽流量,Q为照射到接收器上的太阳辐射能,ρ为密度,V为体积,u为内能,m为质量,Cp为金属热容,h为焓值,T为温度;R为水物质的气体常数,π=p/p*,τ=T*/T,p*=16.53 MPa,T*=1 386 K,系数ni、Ii、Ji见文[19]中的表 3.1;下标s、w、m、t分别表示蒸汽、水、金属和整个系统,仿真对象的参数设置参照文[20].
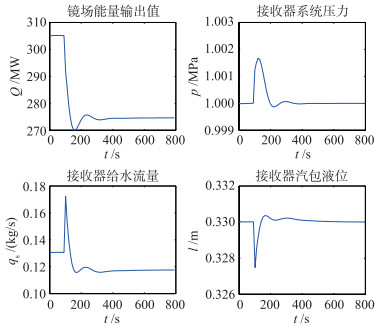
根据系统的参数与特性,系统压力的设定值为1 MPa,液位的设定值为0.33 m,仿真时假设DNI不变,在100 s处加入蒸汽流量阶跃,仿真结果如图 8、9所示.可以看出,当蒸汽流量向上阶跃变化10%时,压力迅速减小,引起汽包内的水沸腾加剧,导致液位迅速升高,但这是假性升高,导致控制液位的给水流量迅速减小.此时为了增加压力,镜场输出的能量要增大,这需要镜场调度来实现,压力恢复的过程中,液位也回到正常水平,给水流量做出相应的调整,最终通过给水流量和镜场输出能量的控制将压力和液位稳定在设定值;当蒸汽流量向下阶跃变化10%时,压力随之上升,液位下降,镜场输出的能量和给水流量通过相应的调整将压力和液位稳定在设定值.从图 8、9的控制曲线可以看出,在镜场调度的配合下,控制器具有良好的跟踪能力,说明利用镜场调度的方法可以对接收器参数进行良好的控制.

|
| 图 8 蒸汽流量向上阶跃10%各变量动态变化 Figure 8 Dynamic changes when steam flow step up to 110% |
|
| 图 9 蒸汽流量向下阶跃10%各变量动态变化 Figure 9 Dynamic changes when steam flow step down to 90% |
上述问题分别采用贪婪—粒子群优化算法、粒子群优化算法和贪婪算法进行求解,结果对比见表 1和表 2. 表 1中,误差Ep和EQ分别表示压力和能量输出值的误差绝对值积分,计算公式如式(13)、式(14)所示. i表示第i次调度,下标s代表设定值,Δt表示优化时间间隔,此处取10 s.
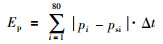
|
(13) |
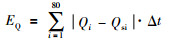
|
(14) |
| 算法 | 误差 | |
| Ep | EQ | |
| 贪婪算法 | 0.036 1 | 539.4 |
| 粒子群算法 | 0.031 9 | 417.8 |
| 贪婪—粒子群优化算法 | 0.031 7 | 417.8 |
| 算法 | 求解时间/s (蒸汽流量阶跃 增大10%) |
求解时间/s (蒸汽流量阶跃 减小10%) |
| 贪婪算法 | 0.089 4 | 0.095 1 |
| 粒子群优化算法 | 1 109 | 1 076 |
| 贪婪—粒子群优化算法 | 11.180 7 | 37.846 |
由表 1可以看出,采用粒子群算法和贪婪—粒子群优化算法得到的压力控制结果精度接近且由采用贪婪算法得到的结果.由表 2可以看出,贪婪—粒子群优化算法求解速度虽比贪婪算法慢,但较粒子群优化算法有明显的提高,能够满足电站对镜场优化调度的求解速度要求,其中蒸汽流量阶跃减小10%的求解时间比蒸汽流量阶跃增大10%的求解时间大,这是因为蒸汽流量阶跃减小时镜场所需能量减小,这使得固定区的镜子数减少,调度区的镜子数增大,也就是决策变量增大,求解时间变长.
由此可见,本文调度方法不仅能够有效地满足系统固定的能量需求,还能够在速度和精度上有效满足动态的能量需求.
4 结论塔式太阳能发电站是通过镜场聚集能量的,由于日照的不稳定性,使得镜场反射到接收器上的能量随之多变,所以镜场的能量调度对电站的稳定性及安全运行有着重要的意义.
本文提出了一种基于整数规划的镜场能量调度模型,并采用贪婪—粒子群优化算法求解调度模型.在仿真研究中,分为系统需求能量固定和能量需求实时变化两种情况,在能量需求固定的情况下,DNI随时间变化,利用镜场调度优化算法得出镜场输出的能量能够较精确地满足设定值,证明了调度方法的正确性;在能量需求随时间变化的情况下,利用镜场输出的能量值实时控制接收器内的压力,能量为控制变量,压力为被控变量,蒸汽流量为扰动变量,表明了基于整数规划的调度方法能够实时满足不同的能量需求.在后续的研究中,可以考虑上一时刻的定日镜的状态,进一步降低定日镜的操作成本;还可以考虑接收器表面能量分布,避免局部过热现象;另外,实际环境的不确定性也是重要的考虑因素,如天气变化、定日镜实际反射的能量与计算能量的差别等,从而为实际的电站运营维护提供依据.
| [1] | 赵军, 李新国, 陈雁. 太阳能热发电技术及其在我国的应用前景[J]. 太阳能 , 2005 (4) : 36–37. Zhao J, Li X G, Chen Y. Solar thermal power technology and its application prospects in China[J]. Solar Energy , 2005 (4) : 36–37. |
| [2] | Behar O, Khellaf A, Mohammedi K. A review of studies on central receiver solar thermal power plants[J]. Renewable and Sustainable Energy Reviews , 2013, 23 (4) : 12–39. |
| [3] | 丁婷婷, 祝雪妹. 智能算法在聚光镜场调度中的应用研究[J]. 太阳能学报 , 2014, 35 (11) : 2139–2144. Ding T T, Zhu X M. Application research of heliostats field scheduling with intelligent algorithm[J]. Acta Energiae Solaris Sinica , 2014, 35 (11) : 2139–2144. |
| [4] | 辛秋霞, 卞新高, 杨缝缝. 塔式太阳能热发电系统镜场调度方法的研究[J]. 太阳能学报 , 2010, 31 (3) : 317–322. Xin Q X, Bian X G, Yang F F. Research on dispatching heliostats in solar power tower plant[J]. Acta Energiae Solaris Sinica , 2010, 31 (3) : 317–322. |
| [5] | Gallego A J, Fele F, Camacho E F. On the optimization of irradiance distribution in solar tower plants with flat receivers[C]//Control Conference(ECC). Piscataway, NJ, USA:IEEE, 2014:2496-2501. |
| [6] | Fernandez N, Street A, Montenon A, et al. A scheduling optimization model for sun tracking of an autonomous heliostat[C]//PowerTech(POWERTECH). Piscataway, NJ, USA:IEEE, 2013:1-6. |
| [7] | Hamza K, Gandhi U, Saitou K. Optimal scheduling of parabolic heliostats aim targets in a mini-tower solar concentrator system[C]//ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Washington, DC, USA:American Society of Mechanical Engineers, 2011:351-358. |
| [8] | Besarati S M, Goswami D Y, Stefanakos E K. Optimal heliostat aiming strategy for uniform distribution of heat flux on the receiver of a solar power tower plant[J]. Energy Conversion and Management , 2014, 84 : 234–243. DOI:10.1016/j.enconman.2014.04.030 |
| [9] | Salomé A, Chhel F, Flamant G, et al. Control of the flux distribution on a solar tower receiver using an optimized aiming point strategy:application to themis solar tower[J]. Solar Energy , 2013, 94 (4) : 352–366. |
| [10] | 郭铁铮, 刘国耀, 刘德有, 等. 塔式太阳能吸热器过热评价模型及镜场调度方法研究[J]. 太阳能学报 , 2014, 35 (1) : 166–170. Guo T Z, Liu G Y, Liu D Y, et al. Research on superheated evaluation model of receiver on solar power tower plant and dispatching methods of heliostats field[J]. Acta Energiae Solaris Sinica , 2014, 35 (1) : 166–170. |
| [11] | 谢飞.塔式太阳能热电系统定日镜场光学仿真与应用研究[D].杭州:浙江大学, 2013. Xie F, Optical simulation of heliostat feild in solar tower power system and its application[D]. Hangzhou:Zhejiang University, 2013. http://cdmd.cnki.com.cn/article/cdmd-10335-1013185658.htm |
| [12] | 陈将.塔式太阳能热电系统的聚光仿真与聚焦策略优化[D].杭州:浙江大学, 2015. Chen J. Concentrating simulation and aiming strategy optimization of solar tower power system[D]. Hangzhou:Zhejiang University, 2015. |
| [13] | Edmonds J. Matroids and the greedy algorithm[J]. Mathematical Programming , 1971, 1 (1) : 127–136. DOI:10.1007/BF01584082 |
| [14] | Eberhart R C, Shi Y. Particle swarm optimization:developments, applications and resources[C]//Proceedings of the 2001 Congress on Evolutionary Computation. Piscataway, NJ, USA:IEEE, 1988(1):81-86. |
| [15] | 沈艳, 郭兵, 古天祥. 粒子群优化算法及其与遗传算法的比较[J]. 电子科技大学学报 , 2006, 34 (5) : 696–699. Shen Y, Guo B, Gu T X. Particle swarm optimization algorithm and comparison with genetic algorithm[J]. Journal of Electronic Science and Technology , 2006, 34 (5) : 696–699. |
| [16] | Kennedy J, Eberhart R C. A discrete binary version of the particle swarm algorithm[C]//Systems, Man, and Cybernetics, 1997. Computational Cybernetics and Simulation. Piscataway, NJ, USA:IEEE, 1997:4104-4108. |
| [17] | Valenzuela L, Zarza E, Berenguel M, et al. Control scheme for direct steam generation in parabolic troughs under recirculation operation mode[J]. Solar energy , 2006, 80 (1) : 1–17. DOI:10.1016/j.solener.2005.09.009 |
| [18] | Zarza E, Valenzuela L, Leon J, et al. Direct steam generation in parabolic troughs:Final results and conclusions of the DISS project[J]. Energy , 2004, 29 (5) : 635–644. |
| [19] | 瓦格纳W, 克鲁泽A. 水和蒸汽的性质[M]. 北京: 科学出版社 ,2003 . Wagner W, Kruse A. Properties of water and steam[M]. Beijing: Science Press , 2003 . |
| [20] | 嵇婷.自然循环锅炉汽水系统模拟与参数估计[D].杭州:浙江大学, 2013. Ji T. Simulation and parameter estimation of natural circulation drum boiler steam-water system[D]. Hangzhou:Zhejiang University, 2013. http://cdmd.cnki.com.cn/article/cdmd-10335-1013185685.htm |



