2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
1 引言
随着企业信息化的深入发展,许多企业实施了制造执行系统(manufacturing execution system,MES),MES的核心部分作业计划与调度功能是根据有限的资源对生产作业进行排序,以满足一定的优化目标.因为作业排产在不增加任何生产资源的情况下通过合理分配生产资源就能提高设备的利用率、缩短生产周期、降低在制品库存等,备受研究者的关注.而实际的企业信息化系统在支持详细的作业排产方面有所欠缺,也使作业排产成为一个亟待解决的关键问题.
求解作业排产问题的方法包括经典的运筹学方法、基于规则的启发式算法及最近兴起仿生智能优化方法.其中运筹学方法计算量大,适于小规模问题;基于规则的启发式算法能通过规则快速地构造出调度解,针对置换流水车间调度问题(permutation flow-shop scheduling problems,PFSP),经典的方法包括Nawaz Enscore Ham(NEH)方法[1]、Gupta方法[2]、Campbell Dudek Smith(CDS)方法[3]、Palmer方法[4]等,其中NEH方法效果很好.值得指出的是,求解PFSP的方法并不适合求解基于流水线制造单元的允许工序跳跃的问题[5].
由于大多数实际工程问题具有大规模性、不确定性、非线性等特点,用传统的解析方法不能在有限时间内给出一个好的解;近来兴起的仿生智能优化算法由于不受实际工程问题特点的约束且能给出一个近似最优的解得到广泛的研究与应用,如蚁群算法[6-7]、遗传算法[8-10]、粒子群算法[11-14]、仿杂草生长算法[15]、人工蜜蜂群算法(artificial bee colony,ABC)[16]等.与其它基于种群的智能算法相比,人工蜜蜂群算法[17-18]因其设置的控制参数少、优化效果突出等优点常被作为算法的主框架. Karaboga与Basturk将ABC算法的性能与遗传算法(genetic algorithm,GA)、粒子群算法(particle swarm algorithm,PSO)、粒子群进化算法(particle swarm inspired evolutionary algorithm,PS-EA)和差分算法(differential evolution,DE)[19-21]在一系列测试问题上进行了比较,结果显示,ABC性能明显好于其它算法,在收敛速度与收敛精度方面具有很大的优势.在参数设置方面,除了评估次数与种群大小两个参数外,遗传算法还要设置交叉因子与变异因子,粒子群算法需要设置两个学习因子与惯性权重,人工蜜蜂群算法只需要设置食物源的适应度未改进的次数上限一个参数.特别当解决实际的工程问题时,多个控制参数造成很难找到适当的值满足求解质量.另外,当应用智能优化算法求解作业排产问题时还必须明确排产与业务目标之间的关系.文[22-23]综述了柔性流水线调度问题,其中多以求解最小最大完工时间为目标.而资金流转率是一项衡量企业决策的关键绩效指标,它反映企业资金流转的速度,在一定的资金规模下,资金周转率越高,企业的营业收入就越多.本文的研究以铝挤压加工为背景的,而在铝挤压车间层面上,车间的生产管理是提高生产效率、降低生产成本、加快资金流转的重要一环,合理的作业排产可以减少产品加工总流经时间降低在制品库存,减少能耗从而提高企业收益.
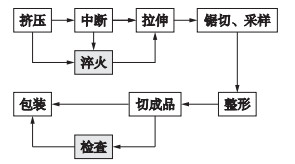
典型的铝挤压涉及工序包括挤压、中断、淬火、拉伸、锯切采样、整形、切成品、检查、包装等;其中挤压与中断一般连续加工,可以看作一个加工中心.在实际生产中,由于订单产品对合金与型号等要求不同,产品加工可能走不同的工艺路线,如图 1所示,有的产品工艺路线依次经过挤压、中断、拉伸、锯切采样、整形、切成品、包装;有的产品工艺路线依次经过挤压、淬火、拉伸、锯切采样、整形、切成品、检查、包装.
|
| 图 1 铝挤压加工流程 Figure 1 Aluminum extrusion processing flow |
在密切结合铝挤压生产特点的基础上,将铝挤压排产问题抽象为两类基于批量组织生产的流水车间调度问题.然后对原始的人工蜜蜂群算法的解产生策略进行改进以适合求解作业排产问题,形成离散版的人工蜜蜂群算法.为验证该算法的优化能力,将其在40个Taillard实例上进行了测试,并与NEH、PSO算法进行了比较,测试结果表明文中提出算法能够有效的解决PFSP问题.最后采用该算法以减少产品加工总流经时间为目标对两类挤压作业计划排产问题求解,求解结果要好于经典的构造型方法NEH.
2 作业排产建模为了减少设备的准备时间,铝挤压车间在接到生产计划部下发的计划后,通常会按照订货产品对应的模具型号、交货期等组织成批次进行生产.同一型号的工件安排在一个批次中;每个批次中的工件都是连续加工,在一个批次中的某个工件完成即可送到该批次工艺流程中下一个工序加工;同一个批次的工件在某个工序的紧后工序最早开工时间等于当前工序的开工时间加上该批次中一个工件的加工时间;由于单个工件的加工时间相对于一个批次的总加工时间来说比较短,可以认为一个批次在某工序的紧后工序的最早开工时间与当前工序的开工时间一致.
假设π={π1,π2,…,πn}为所求解作业排产问题一个调度序列;P(πi,j),i=1,…,n,j=1,…,m为批次i在机器j上的加工时间;C(πi,j)为批次πi在机器j上的完工时间;begin(πi,j)为批次πi在机器j上的开工时间;TFT为总流经时间.
在实际生产中的一个计划周期内,生产车间接到订单的产品所走工艺路线可能一致,也可能不同.针对工艺路线一致的情况(本文中称为一类问题),铝作业排产可以用一个基于批次加工的置换流水车间调度问题描述:

|
(1) |
针对工艺路线不一致的情况(本文中称为二类问题),由于每台设备加工的工件不同,如果还采用置换流水车间调度求解策略可能引起某设备强制空闲.由于铝挤压第1个设备挤压机是必走工序,所以第1个设备仍然采用求解置换流水车间调度的方法,后续设备根据实际情况采用先来先服务的策略进行排产.两种情况下的目标都是寻找一个调度序列使总流经时间(TFT)最小.
3 基于人工蜜蜂群算法的作业排产原始的人工蜜蜂群算法在连续的搜索空间有很好的优化效果,对于离散的搜索空间不能直接使用,需要对其进行改进.根据需要解决的作业排产问题修改解的表达与新解的产生方式.在改进版的人工蜜蜂群算法中,每个食物源表示一个调度序列.
3.1 编码对于基于种群的算法,必须对个体编码进行设计以表达调度问题的解.对于批次数目为n的排产问题,个体编码用一个n维向量表示,每个维度上的值就代表了批次序号.比如,对于10个批次的排产问题,个体[9, 10, 6, 5, 3, 2, 4, 1, 8, 7]表示加工顺序为9,10,6,5,3,2,4,1,8,7.
3.2 算法实现与流程人工蜜蜂向邻居学习采用PBX方式进行学习[24],如图 2所示;从当前个体中随机选择批次,每个批次选中的概率是50%;被选中的批次直接继承到新个体中;对于没有选中的批次,按照邻居个体中的位置从左到右插入新个体的空白位置.

|
| 图 2 PBX方式 Figure 2 PBX way |
算法步骤如表 1所示.
算法中的评估食物源就是求解群体中每个个体的目标函数.初始化食物源位置就是按照3.1节的编码方式将要排产的作业任务转换为加工顺序.
算法中的目标函数是最小化最大完工时间(f=min C(πn,m))或者最小化加工总流经时间(f=min TFT).目标函数越小,适应度越大.取适应度为fitnessi=fmax-fi.算法中的概率选择公式如式(2)所示,其中fitnessi是第i个食物源的适应度:

|
(2) |
为了验证文中的ABC算法求解PFSP的性能,进行3项实验.实验1在一些著名的基准测试问题上以最小加工总流经时间为目标进行验证.实验2与实验3分别用实际生产任务数据进行验证.在所有实验中,人工蜜蜂群算法种群大小设置为设备数量的10倍,食物源的适应度未改进的次数达到预设的参数100,雇佣蜂变成侦查蜂.算法停止条件采用评估次数达到预设的参数.算法在每个实例上运行10次.所有算法采用Java编码,计算机配置为Intel Core双核2.20 GHz CPU,1 G内存.
4.1 实验1本实验中采用40个Taillard实例[25],包括20×5、20×10、20×20和50×5四组,每组10个实例.实验结果用最佳相对偏差BRE(best relative error)和平均相对偏差ARE(average relative error)表示.
最佳相对偏差BRE:

|
平均相对偏差ARE:

|
其中,C*为各实例目前已知的最优结果,Cbest为各算法所求得的最好结果.在实验中将ABC、PSO及NEH方法进行了比较. PSO算法的参数采用文[11]的原始设置.
表 2给出各个算法在40个Taillard测试实例上的最佳相对偏差.其中,C*为文[26]中实例目前已知的最优结果,PSO_BRE、ABC_BRE及NEH_BRE为各算法的相对百分偏差.从表 2中可以看出,ABC在所有测试实例上取得了最好的效果.
| instance | n | m | C* | PSO_BRE | ABC_BRE | NEH_BRE |
| ta001 | 20 | 5 | 14 226 | 0.267 | -1.300 | 3.845 |
| ta002 | 20 | 5 | 15 446 | 0.369 | -1.625 | 2.324 |
| ta003 | 20 | 5 | 13 676 | 0.080 | -2.742 | 1.280 |
| ta004 | 20 | 5 | 15 750 | -0.559 | -1.848 | 1.321 |
| ta005 | 20 | 5 | 13 633 | 0.844 | -0.763 | 2.391 |
| ta006 | 20 | 5 | 13 265 | 2.473 | -1.070 | 2.111 |
| ta007 | 20 | 5 | 13 774 | -1.118 | -1.561 | 7.238 |
| ta008 | 20 | 5 | 13 968 | 1.933 | -0.143 | 6.007 |
| ta009 | 20 | 5 | 14 456 | 2.124 | -1.114 | 2.553 |
| ta010 | 20 | 5 | 13 036 | 0.921 | -0.713 | 5.654 |
| ta011 | 20 | 10 | 21 207 | 2.447 | -1.188 | 2.787 |
| ta012 | 20 | 10 | 22 927 | -0.750 | -2.124 | 3.315 |
| ta013 | 20 | 10 | 20 072 | 0.593 | -1.191 | 0.488 |
| ta014 | 20 | 10 | 18 857 | 1.432 | -0.583 | 0.817 |
| ta015 | 20 | 10 | 18 939 | -0.459 | -1.515 | 2.666 |
| ta016 | 20 | 10 | 19 608 | 0.602 | -1.831 | 2.173 |
| ta017 | 20 | 10 | 18 723 | 1.143 | -1.923 | 3.653 |
| ta018 | 20 | 10 | 20 504 | 0.195 | -1.010 | 7.238 |
| ta019 | 20 | 10 | 20 561 | 1.663 | -1.123 | 5.374 |
| ta020 | 20 | 10 | 21 506 | -0.623 | -0.795 | 3.041 |
| ta021 | 20 | 20 | 34 119 | 0.516 | -1.454 | 3.702 |
| ta022 | 20 | 20 | 31 918 | 0.482 | -1.037 | 1.908 |
| ta023 | 20 | 20 | 34 552 | -0.654 | -1.829 | 0.463 |
| ta024 | 20 | 20 | 32 159 | -0.227 | -1.406 | 2.198 |
| ta025 | 20 | 20 | 34 990 | -0.009 | -1.237 | 1.906 |
| ta026 | 20 | 20 | 32 734 | 0.330 | -0.519 | 3.397 |
| ta027 | 20 | 20 | 33 449 | 0.093 | -1.193 | 2.559 |
| ta028 | 20 | 20 | 32 611 | 0.386 | -0.475 | 4.670 |
| ta029 | 20 | 20 | 34 084 | -0.229 | -1.420 | 3.004 |
| ta030 | 20 | 20 | 32 537 | 0.596 | -0.845 | 4.444 |
| ta031 | 50 | 5 | 65 663 | 4.395 | -2.201 | 10.677 |
| ta032 | 50 | 5 | 68 664 | 7.333 | -0.048 | 10.864 |
| ta033 | 50 | 5 | 64 378 | 7.694 | -0.800 | 9.601 |
| ta034 | 50 | 5 | 69 795 | 7.114 | -1.229 | 7.407 |
| ta035 | 50 | 5 | 70 841 | 6.437 | -1.208 | 5.044 |
| ta036 | 50 | 5 | 68 084 | 6.032 | -1.016 | 4.368 |
| ta037 | 50 | 5 | 67 186 | 3.572 | -0.246 | 6.902 |
| ta038 | 50 | 5 | 65 582 | 7.220 | -1.195 | 6.058 |
| ta039 | 50 | 5 | 63 968 | 7.447 | -0.975 | 6.442 |
| ta040 | 50 | 5 | 70 273 | 3.478 | -0.847 | 9.123 |
表 3给出了各个算法在Taillard测试实例上的平均相对偏差. 图 3给出各个算法在Taillard实例上的平均相对偏差的折线图.从表 3可以看出,在20×5、20×10、20×20和50×5四组实例上,ABC都取得了最好的效果. 图 3以折线图的形式给出了直观的展示.
| 问题 | 20×5 | 20×10 | 20×20 | 50×5 |
| PSO_ARE | 0.733 | 0.624 | 0.129 | 6.072 |
| ABC_ARE | -1.288 | -1.328 | -1.142 | -0.977 |
| NEH_ARE | 3.472 | 3.155 | 2.825 | 7.649 |

|
| 图 3 各算法在Taillard实例上的平均相对偏差折线图 Figure 3 Line chart of ARE with different algorithms on Taillard instances |
一类问题的生产任务数据如表 4所示,有10个批次的作业任务,这10个批次所走工艺路线一致,表中给出了每个批次的加工时间,每个批次的工艺路线取自某挤压厂的实际工艺流程;采用本文提出的人工蜜蜂群算法与经典的NEH算法对数据进行求解.
| 批次号 | 标识 | 挤压机 | 拉伸机 | 锯切机 | 整形机 | 成品锯 | 包装机 |
| PC15061902-1 | 1 | 174 | 121 | 183 | 102 | 190 | 150 |
| PC15061903-1 | 2 | 120 | 176 | 174 | 199 | 160 | 115 |
| PC15061904-1 | 3 | 167 | 148 | 160 | 166 | 138 | 130 |
| PC15061905-1 | 4 | 97 | 76 | 64 | 110 | 181 | 173 |
| PC15061906-1 | 5 | 87 | 86 | 80 | 90 | 83 | 75 |
| PC15061907-1 | 6 | 80 | 42 | 99 | 70 | 90 | 93 |
| PC15061908-1 | 7 | 69 | 72 | 54 | 80 | 90 | 160 |
| PC15061909-1 | 8 | 69 | 120 | 24 | 96 | 89 | 62 |
| PC15061910-1 | 9 | 50 | 88 | 46 | 63 | 76 | 150 |
| PC15061911-1 | 10 | 97 | 74 | 82 | 53 | 61 | 95 |
采用NEH对表 4所列问题求解,10次求解后最优的排产顺序为5,7,6,10,8,9,4,2,3,1;总流经时间是6 537. 图 4为NEH算法的排产的甘特图.

|
| 图 4 NEH算法求解一类问题的甘特图 Figure 4 Gantt chart for the first problem using NEH |
采用人工蜜蜂群算法,种群大小为60,10次求解后最优的排产顺序为:5,7,6,8,10,9,1,2,3,4;总流经时间是6 478. 10次运行时间大约2 min. 图 5为人工蜜蜂群算法排产的甘特图.

|
| 图 5 人工蜜蜂群算法求解一类问题的甘特图 Figure 5 Gantt chart for the first problem using ABC |
两种算法求解结果表明,人工蜜蜂群算法比NEH算法的总流经时间少59个单位时间.
4.3 实验3二类问题的生产任务数据如表 5所示,有12个批次的作业任务,这12个批次所走工艺路线不完全一致,表中给出了每个批次的加工时间,“-”表示不在某设备上加工.每个批次的工艺路线取自某挤压厂的实际工艺流程;采用本文提出的人工蜜蜂群算法与经典的NEH算法对数据进行求解.
| 批次号 | 标识 | 挤压机 | 淬火炉 | 拉伸机 | 锯切机 | 整形机 | 成品锯 | 仪器仪表 | 包装机 |
| PC15071902-1 | 1 | 170 | 150 | 120 | 103 | 102 | 100 | 120 | 150 |
| PC15071903-1 | 2 | 120 | - | 176 | 174 | 199 | 160 | - | 115 |
| PC15071904-1 | 3 | 170 | 160 | 158 | 120 | 160 | 140 | 120 | 130 |
| PC15071905-1 | 4 | 97 | - | 76 | 64 | 110 | 181 | - | 173 |
| PC15071906-1 | 5 | 87 | - | 86 | 80 | 90 | 83 | - | 75 |
| PC15071907-1 | 6 | 80 | - | 42 | 99 | 70 | 90 | - | 93 |
| PC15071908-1 | 7 | 169 | 120 | 87 | 65 | 80 | 92 | 125 | 130 |
| PC15071909-1 | 8 | 79 | 130 | 120 | 54 | 106 | 88 | 77 | 100 |
| PC15071910-1 | 9 | 50 | - | 88 | 46 | 63 | 76 | - | 150 |
| PC15071911-1 | 10 | 97 | - | 74 | 82 | 53 | 61 | - | 95 |
| PC15071912-1 | 11 | 99 | - | 76 | 89 | 97 | 78 | - | 100 |
| PC15071913-1 | 12 | 140 | 121 | 89 | 99 | 87 | 120 | 126 | 130 |
| 注:“-”表示不在某设备上加工. | |||||||||
采用NEH对表 5所列问题求解,10次求解后最优的排产顺序为:10,5,4,6,11,9,2,12,8,7,1,3;总流经时间是9 335. 图 6为NEH算法的排产的甘特图.

|
| 图 6 NEH算法求解二类问题的甘特图 Figure 6 Gantt chart for the second problem using NEH |
采用人工蜜蜂群算法对表 5所列问题求解,种群大小为80,10次求解后最优的排产顺序为:11,6,9,5,10,2,12,8,7,3,4,1;总流经时间是8 981. 10次运行时间大约2分钟. 图 7为人工蜜蜂群算法排产的甘特图.

|
| 图 7 人工蜜蜂群算法求解二类问题的甘特图 Figure 7 Gantt chart for the second problem using ABC |
两种算法求解结果表明,人工蜜蜂群算法比NEH算法的总流经时间少354个单位时间.
5 结论铝挤压作业排产是计划员将作业计划下达到生产车间之前的关键步骤,优化的作业排产顺序能有效地提高生产效率,减少能量消耗.而作业计划的排序问题已经被证明是NP难问题,许多算法被提出来解决此问题.本文对人工蜜蜂群算法的算子重新定义,形成离散版的人工蜜蜂群算法.为验证该算法的优化能力,将其在4组Taillard实例上进行了测试,并与NEH、PSO算法进行了比较,测试结果表明本文中提出算法能够有效地解决PFSP问题.根据铝挤压的生产与工艺特点将铝挤压排产问题抽象为两类基于批量组织生产的流水车间调度问题,并以总流经时间最小为目标采用离散的人工蜜蜂群算法求解问题.通过仿真实验与经典的构造型方法NEH对比表明了提出的算法能够给出更好的调度序列.
| [1] | Nawaz M, Enscore J E, Ham I. A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem[J]. Omega , 1983, 11 (1) : 91–95. DOI:10.1016/0305-0483(83)90088-9 |
| [2] | Gupta J. A functional heuristic algorithm for the flow shop scheduling problem[J]. Operations Research , 1971, 22 (1) : 39–47. DOI:10.1057/jors.1971.18 |
| [3] | Garey M R, Johnson S, Sethi R. The complexity of flow-shop and job shop scheduling[J]. Mathematics of Operations Research , 1976, 1 (1) : 117–29. |
| [4] | Palmer D S. Sequencing jobs through a multistage process in the minimum total time:A quick method of obtaining a near optimum[J]. Operations Research Quarterly , 1965, 16 (1) : 101–107. DOI:10.1057/jors.1965.8 |
| [5] | Pugazhendhi S, Thiagarajan S, Rajendran C, et al. Performance enhancement by using non-permutation schedules in flow line-based manufacturing systems[J]. Computers and Industrial Engineering , 2002, 44 (1) : 133–157. |
| [6] | Marimuthu S, Ponnambalam S G, Jawahar N. Threshold accepting and ant-colony optimization algorithm for scheduling m-machine flow shop with lot streaming[J]. Journal of Material Processing Technology , 2009, 209 (2) : 1026–1041. DOI:10.1016/j.jmatprotec.2008.03.013 |
| [7] | 闫振国, 李原, 张杰, 等. 一种飞机装配作业批量排产的图解蚁群算法[J]. 计算机集成制造系统 , 2010, 16 (7) : 1437–1443. Yan Z G, Li Y, Zhang J, et al. Graph-based ant colony algorithm for aircraft assembly batch scheduling[J]. Computer Integrated Manufacturing Systems , 2010, 16 (7) : 1437–1443. |
| [8] | Nagano M S, Ruiz R, Lorena L A N. A constructive genetic algorithm for permutation flow shop scheduling[J]. Computers & Industrial Engineering , 2008, 55 (1) : 195–207. |
| [9] | Reeves C, Yamada T. Genetic algorithms, path relinking and the flowshop sequencing problem[J]. Evolutionary Computation , 1998, 6 (1) : 45–60. DOI:10.1162/evco.1998.6.1.45 |
| [10] | Ribeiro Filho G, Nagano M S, Lorena L A N. Evolutionary clustering search for flow time minimization in permutation flow shop[M]//Lecture Notes in Computer Science:vol. 4771. Berlin, Germany:Springer-Verlag, 2007:333-340. |
| [11] | Tasgetiren M F, Liang Y C, Sevkli M, et al. A particle swarm optimization algorithm for makespan and total flowtime minimization in the permutation flowshop sequencing problem[J]. European Journal of Operational Research , 2007, 177 (3) : 1930–1947. DOI:10.1016/j.ejor.2005.12.024 |
| [12] | Hajinejada D, Salmasib N, Mokhtari R. A fast hybrid particle swarm optimization algorithm for flow shop sequence dependent group scheduling problem[J]. Scientia Iranica , 2011, 18 (3) : 759–764. DOI:10.1016/j.scient.2011.05.023 |
| [13] | Tseng C T, Liao C J. A discrete particle swarm optimization for lot-streaming flow shop scheduling problem[J]. European Journal of Operational Research , 2008, 191 (2) : 360–373. DOI:10.1016/j.ejor.2007.08.030 |
| [14] | 乔俊飞, 王超, 魏静. 一种具有局部搜索的自适应粒子群算法[J]. 信息与控制 , 2015, 44 (4) : 385–392. Qiao J F, Wang C, Wei J. An adaptive particle swarm optimization algorithm with local search[J]. Information and Control , 2015, 44 (4) : 385–392. |
| [15] | 石小秋, 石宇强, 袁雪娇. 离散多种群入侵杂草优化算法求解柔性作业车间调度问题[J]. 信息与控制 , 2015, 44 (2) : 238–243. Shi X Q, Shi Y Q, Yuan X J. Invasive weed optimization algorithm with discrete multi-population for the flexible job-shop scheduling problem[J]. Information and control , 2015, 44 (2) : 238–243. |
| [16] | Karaboga D. An idea based on honey bee swarm for numerical optimization[R]. Technical Report TR06, Turkey:Computer Engineering Department, Erciyes University, 2005. |
| [17] | Karaboga D. A new design method based on artificial bee colony algorithm for digital ⅡR filters[J]. Journal of the Franklin Institute , 2009, 346 (4) : 328–348. DOI:10.1016/j.jfranklin.2008.11.003 |
| [18] | Karaboga D, Akay B. A comparative study of artificial bee colony algorithm[J]. Applied Mathematics and Computation , 2009, 214 (1) : 108–132. DOI:10.1016/j.amc.2009.03.090 |
| [19] | Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization:Artificial bee colony(ABC) algorithm[J]. Journal of Global Optimization , 2007, 39 (3) : 459–471. DOI:10.1007/s10898-007-9149-x |
| [20] | Karaboga D, Basturk B. On the performance of artificial bee colony(ABC) algorithm[J]. Applied Soft Computing , 2008, 8 (1) : 687–697. DOI:10.1016/j.asoc.2007.05.007 |
| [21] | Akay B, Karaboga D. Artificial bee colony algorithm for large-scale problems and engineering design optimization[J]. Journal of Intelligent Manufacturing , 2012, 21 (21) : 1–14. |
| [22] | Ruiz R, Vázquez-Rodríguez J A. The hybrid flow shop scheduling problem[J]. European Journal of Operational Research , 2010, 205 (1) : 1–18. DOI:10.1016/j.ejor.2009.09.024 |
| [23] | Ribas I, Leisten R, Framiñan J M. Review and classification of hybrid flow shop scheduling problems from a production system and a solutions procedure perspective[J]. Computers & Operations Research , 2010, 37 (8) : 1439–1454. |
| [24] | Kellegoz T, Toklu B. Comparing efficiencies of genetic crossover operations for one machine total weighted tardiness problem[J]. Applied Mathematics and Computation , 2008, 199 (2) : 590–598. DOI:10.1016/j.amc.2007.10.013 |
| [25] | Taillard E. Benchmarks for basic scheduling problems[J]. European Journal of Operational Research , 1993, 64 (2) : 278–285. DOI:10.1016/0377-2217(93)90182-M |
| [26] | Liu J, Reeves C R. Constructive and composite heuristic solutions to the P//∑Ci scheduling problem[J]. European Journal of Operational Research , 2001, 132 (2) : 439–452. DOI:10.1016/S0377-2217(00)00137-5 |



