2. 山东科技大学信息科学与工程学院, 山东 青岛 266590 ;
3. 大庆油田采油工程研究院举升研究室, 黑龙江 大庆 163318
2. College of Information Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China ;
3. Lifting Research Office, Daqing Production Engineering Research Institute, Daqing 163318, China
1 引言
示功图是抽油机驴头不断上下往复运动,由载荷和位移构成的闭合连续曲线,轮廓特征中不仅隐含了抽油机中丰富的机、泵、杆等设备的工作状态信息,而且可以实时反映砂、蜡、气、油、水等井内因素的影响,因此通过示功图识别来判断抽油机当前所处工作状态,对于提高抽油机效率、油井产量、安全生产都具有很重要的现实意义[1].人工神经网络(artificial neural network,ANN)具有良好的非线性系统逼近能力,近年来基于ANN的示功图识别诊断方法正逐步取代传统的人工分析[2-4],取得了一定的应用效果,但这些方法的输入都是示功图某些特征信号的离散数据采样点,模型内部只能处理同步瞬时输入,无法体现连续信号的时间累积效应、易丢失细节信息,辨识精度较低.
过程神经元网络(process neural network,PNN)是由何新贵院士等提出的一种神经网络模型,模型输入、输出和连接权都可以是与时间有关的函数,在隐层的过程神经元中完成输入信号的空间聚合和时间累积,在系统逼近时放宽了输入信号的同步瞬时限制,提高了输入信号的时间累积效应,拓宽了神经网络的应用领域[5-6].从提出至今,已经出现多种模型,如小波[7]、量子[8]、分段式[9]等,目前应用于时间序列预测[10]、故障诊断[11]、非线性系统建模[12]等的实际问题中,取得了较好的效果.学习算法方面,为简化时空聚合运算,文[13]通过引入正交基函数,将训练转化为基函数系数的学习,但该算法需要计算复杂的梯度信息,存在对初值敏感、计算量大、易陷入局部最小值等缺点,使PNN在应用方面受到了很大限制. 2004年,Huang等提出了一种新的单隐层前馈神经网络学习算法,学习速度快,因此称为极限学习机(extreme learning machine,ELM)[14],并通过实验证明可极大提高神经网络的学习速度(通常10倍以上)[15-16],避免梯度下降法的众多问题,目前已经成为国内外的研究热点.由于ELM学习速度快、泛化性能好,已在故障诊断、模式识别等领域的实际应用中崭露头角[17-20].
综上所述,本文为提高抽油机示功图的诊断识别精度,提出一种极限学习离散过程神经元网络模型(ELM discrete process neural network,ELM-DPNN).不同于连续PNN,输入和权值是离散时间序列,用向量代表每一个过程输入,内部采用三次样条的数值积分来处理离散输入,避免连续PNN因输入拟合带来的解析函数不存在、基函数个数无法确定等问题.同时,为提高模型训练速度,将离散过程神经元按照离散输入和权值进行展开,在模型拓扑结构上进行分析,得出可使用ELM进行模型训练的结论.在隐层离散过程神经元的输入权值和阈值随机赋值后,将隐层输出权值的学习转化为最小二乘问题,通过Moore-Penrose广义逆和隐层输出矩阵来求解隐层输出权值,摒弃梯度下降的迭代调整策略,经矩阵计算即可完成模型训练.最后将ELM-DPNN模型应用于油田实际的示功图识别诊断中,针对常见的5种状态进行识别,模型诊断精度有一定程度的提高,并且学习速度比其它PNN模型提高了4~5倍左右,证明了方法的有效性.
2 极限学习机在单隐层前馈神经网络中,设训练样本X=(x1,x2,…,xN),对应的期望输出为T=(t1,t2,…,tN),模型输入输出映射关系为
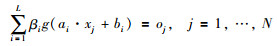
|
(1) |
式中,g(x)为激活函数,ai为输入权重,βi为输出权重,bi为隐层阈值.模型学习目标是使代价函数E最小,E为目标输出和期望输出的误差平方和,如下:
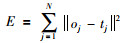
|
(2) |
即存在βi、ai和bi,式(1)可表示为
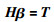
|
(3) |
式中,H是隐层输出矩阵,β为隐层输出权重向量.当前馈神经网络使用梯度下降法学习训练时,存在计算量大、训练速度慢、易陷入局部最小等问题.为解决该问题,Huang提出以下定理:
引理1[14]对任意N个不同样本(xi,ti)、M个隐层节点和一个可导激活函数g,前馈神经网络在ai∈Rn和bi∈Rn任意赋值的情况下,存在可逆的隐层矩阵H,使得方程组有精确解,即E=0.
引理2[14]给点任意N个不同样本(xi,ti)、任意小误差e>0及可导激活函数g,总存在一个包含M个隐层结点的前馈神经网络,使得ai∈Rn和bi∈Rn任意赋值的情况下,误差E≤e.
基于以上两个定理,Huang提出了ELM算法,即前馈神经网络只要在权值和阈值赋值的情况下,能够确定一个具有可逆特性的隐层输出矩阵,完成对系统的逼近,从而将前馈神经网络的训练过程转化为式(3)的最小二乘问题.根据Moore-Penrose广义逆,隐层输出权值为
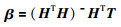
|
(4) |
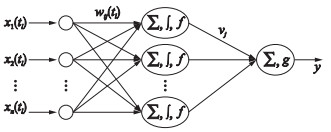
离散过程神经元包括加权、聚合和激励输出三部分,输入用向量代表每一个过程输入,不同于普通神经网络,网络的各维输入是不同时刻的采样值,即为一个离散时间序列,此时单个样本的表述形式不同于普通神经网络的向量,而是一个矩阵.设x1(tl),x2(tl),…,xn(tl)是输入,wij(tl)为权值,模型结构如图 1所示.
|
| 图 1 离散过程神经元网络 Figure 1 The discrete process neural network |
网络的输出与输入间的映射关系为
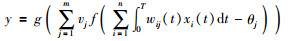
|
(5) |
对于给定K个样本(xk1(tl),xk2(tl),…,xkn(tl);dk),k=1,2,…,K,l=1,2,…,T,网络误差函数可定义为
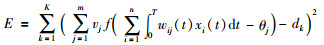
|
离散过程神经元内部使用三次样条数值积分完成离散样本输入和权值之间的时域聚合运算.设[a,b]为积分区间,记xk=a+kh,yk=f(xk),k=0,1,…,n,h=(b-a)/n.边界条件如下:
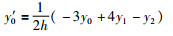
|
(6) |
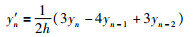
|
(7) |
则三次样条函数可写为
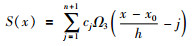
|
(8) |
其中Ω3(x)是样条函数,如下:
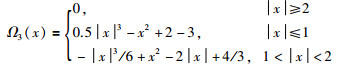
|
(9) |
参数cj的计算如下:
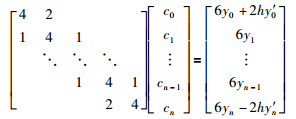
|
(10) |
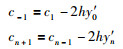
|
(11) |
则被积函数f(x)在[a,b]上的积分,可由三次样条函数S(x)的数值积分获得:
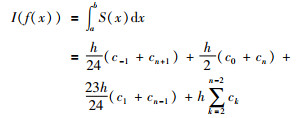
|
(12) |
根据三次样条数值积分,式(5)可写为

|
(13) |
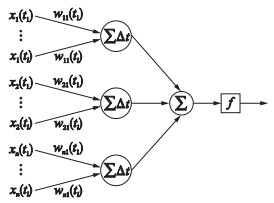
离散过程神经元的输入是时间序列的离散输入,采用三次样条数值积分处理离散样本的时域聚合,根据式(13),对离散过程神经元进行结构展开,如图 2所示.
|
| 图 2 离散过程神经元的展开结构 Figure 2 The expanded structure of discrete process neuron |
离散过程神经元的输入与普通神经元的同步瞬时输入不同,是样本采样时间序列xi(tl)组成的2维矩阵[x1(tl),x2(tl),…,xn(tl)]T.时域聚合部分经过数值积分简化后,离散过程神经元展后开的结构和普通神经元基本相同,因此可使用ELM进行训练.由于离散过程神经元规模较大,n个隐层神经元共有输入权值共有n×n×L个.若采用其它学习算法来训练,计算量大、训练速度慢、且不易收敛,因此研究ELM-DPNN训练问题具有重要意义.
4.2 ELM-DPNN隐层输出矩阵和权值(1)确定隐层节点数量,并对每个隐层神经元的阈值和输入权值向量进行随机赋值.
(2)计算隐层的输出矩阵.
对于给定K个样本(xk1(tl),xk2(tl),…,xkn(tl);dk),k=1,2,…,K,ELM-DPNN的隐层输出矩阵H为
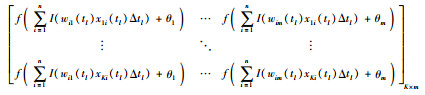
|
(14) |
在矩阵H中,第k行是训练样本中的第k个样本在每个隐层离散过程神经元的输出向量;第j列是对于输入样本中的每个样本在第j个隐层离散过程神经元的输出向量.根据式(3)、式(14),ELM-DPNN输入输出映射关系可写为
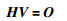
|
(15) |
其中O=[d1,d2,…,dK]K×1T为DPNN期望输出向量,V=[v1,v2,…,vm]m×1T为隐层输出权值向量.
(3)计算隐层与输出层的权值.
ELM-DPNN的隐层输入权值和阈值随机赋值后,训练问题就转会为最小二乘问题,即寻找一组合适的隐层输出权值,使得模型以最小的误差逼近非线性系统.模型的隐层输出权值计算公式为
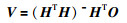
|
(16) |
当H为非奇异方阵时,可以直接求解得到H的逆矩阵.而多数情况下,矩阵H为奇异方阵,则需要求解H的Moore-Penrose广义逆矩阵H+.本文根据奇异值分解(singular value decomposition,SVD)法,将H进行分解:
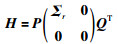
|
(17) |
其中,P是m×m的正交矩阵,Q是n×n的正交矩阵,r是矩阵H的秩,Σr由方阵H的特征值平方根通过对角排列组成. H+的计算公式为
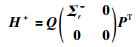
|
(18) |
根据式(16),ELM-DPNN隐层输出权值的计算公式为
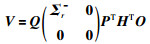
|
(19) |
从式(19)中可以看出,对输入权值和阈值随机赋值后,根据ELM学习算法,通过计算隐层输出矩阵的Moore-Penrose广义逆,可一次求解出隐层输出权值向量,完成网络训练.
5 ELM-DPNN的示功图识别常见的抽油机工作状态有5种,即正常工作、抽油杆断脱、固定凡尔漏失、双凡尔漏失和油杆偏磨.本文主要针对这5种示功图进行诊断识别,数据取自大庆某油矿的无线巡检系统,共包括5种工作状态的482个实测示功图数据.选取其中的400组作为训练样本,使模型达到稳定.剩余的82组作为测试样本,检验模型的诊断泛化能力.
由于每口油井的数据精度和量纲可能不同,在输入模型之前需进行预处理,把原始示功图数据通过归一化的方式规范为统一形式,公式如下:
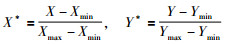
|
(20) |
其中X和Y为原始示功图的位移和载荷,X*和Y*为归一化后的数值.
5.1 模型结构和参数设置(1)为检验本文的ELM-DPNN在示功图识别时的有效性,分别从学习能力和诊断识别精度两个方面进行对比.对比模型包括:文[13]的正交基展开连续PNN(orthogonal basis-based PNN,OBPNN)、文[18]的DEPSO-ELM、文[21]的二次样条PNN(secondary spline PNN,SSPNN).其中ELM-DPNN、OBPNN和SSPNN都是PNN模型,DEPSO-ELM是普通神经网络模型.
(2)示功图数据处理.为减小网络规模,提高训练速度,去除冗余数据,在保持示功图轮廓特征基础上,按照采样点欧式距离的大小,对示功图中原始的308个采样点进行抽稀.首先给定阈值ε>0,设示功图的下死点为起始点P1(x1,y1),沿顺势针方向计算相邻点之间的欧氏距离l.若l≥ε,则该点保留;否则剔除,最后直到起始点为止,最后得到96个位移和载荷数据对.
(3)模型结构参数.对于ELM-DPNN和SSPNN,输入为位移和载荷向量,对于OBPNN则需要首先对位移和载荷按照时间拟合,正交基为勒让德基函数,展开项数L=20,拟合后的“位移—时间”和“载荷—时间”连续函数作为模型输入,因此这三种模型的输入节点为2个.目前关于PNN隐层节点数的确定还未见研究,本文经过多次实验,对不同隐层规模实验,通过训练能力、预测能力最终确定ELM-DPNN隐层节点数为16个,具体见表 2所示.此外对于DEPSO-ELM模型,输入节点为位移和载荷数据,共192个,隐层节点数60. 4种模型的输出节点都为5,即示功图状态类别,每种工况的期望输出如表 1所示.
| 工况类型 | 输出节点的期望值 | ||||
| 节点1 | 节点2 | 节点3 | 节点4 | 节点5 | |
| 正常工况 | 1 | 0 | 0 | 0 | 0 |
| 抽油杆断脱 | 0 | 1 | 0 | 0 | 0 |
| 固定漏失 | 0 | 0 | 1 | 0 | 0 |
| 双凡尔漏失 | 0 | 0 | 0 | 1 | 0 |
| 油杆偏磨 | 0 | 0 | 0 | 0 | 1 |
| 隐层 节点数 |
训练情况 | 预测情况 | |||
| 相关系数 | 均方误差 | 训练时间/s | 相关系数 | 均方误差 | |
| 10 | 0.843 5 | 0.083 8 | 10.625 1 | 0.879 5 | 0.235 57 |
| 12 | 0.924 6 | 0.033 7 | 15.496 0 | 0.908 1 | 0.183 61 |
| 14 | 0.975 2 | 0.016 9 | 19.820 5 | 0.969 2 | 0.101 33 |
| 16 | 0.992 1 | 0.005 9 | 23.692 1 | 0.994 5 | 0.085 01 |
| 18 | 0.992 9 | 0.004 6 | 26.603 3 | 0.984 9 | 0.096 29 |
| 20 | 0.993 7 | 0.003 8 | 31.597 6 | 0.946 1 | 0.127 21 |
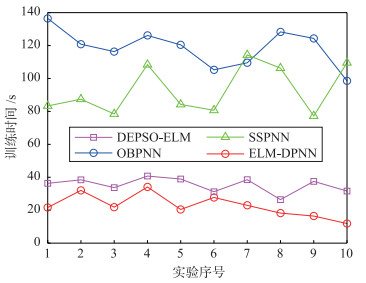
(1)针对4种模型和400组训练样本,各进行10次训练,学习情况对比如表 3所示,图 3是训练时间对比.在训练时间上,可以看出ELM-DPNN在训练时间上比OBPNN和SSPNN的学习速度有了很大提高,达到4~5倍左右,并且略低于DEPSO-ELM.同时ELM-DPNN的收敛能力DEPSO-ELM模型高,训练收敛能力达到70%.
| 诊断模型 | 400组样本的训练情况对比 | 82组测试样本的诊断情况对比 | |||||
| 相关系数 | 平均时间/s | 收敛次数 | 最高识别率/% | 最低识别率/% | 平均识别率/% | 最大误判 | |
| DEPSO-ELM | 0.894 01 | 36.337 | 4 | 82.926 83 | 76.829 27 | 80.121 95 | 19 |
| OBPNN | 0.914 95 | 118.615 | 6 | 92.682 93 | 89.024 39 | 90.975 55 | 9 |
| SSPNN | 0.931 94 | 92.993 | 7 | 96.341 46 | 90.243 90 | 93.414 63 | 8 |
| ELM-DPNN | 0.978 39 | 22.725 | 7 | 98.780 48 | 95.121 95 | 97.804 87 | 4 |
|
| 图 3 4种模型的训练时间对比 Figure 3 Training time comparison among four models |
(2)原因分析:在训练时间上,由于ELM-DPNN采用极限学习,通过采用Moore-Penrose广义逆和SVD分解,利用矩阵计算即可计算出隐层输出权值,完成模型训练,无需计算复杂梯度信息,因此训练速度比OBPNN和SSPNN有了很大提高.而OBPNN由于使用正交基函数展开,同时对输入进行基函数拟合,因此训练时间长. SSPNN由于不需要输入函数拟合,也无需基函数展开,但需要计算梯度,因此训练时间虽然低于OBPNN,却明显高于ELM-DPNN.但3种PNN模型由于内部隐层过程神经元的时空聚合机制,使得模型收敛能力均要高于DEPSO-ELM. DEPSO-ELM虽采用极限学习,但是输入节点多,模型规模大,优化种群中的个体维数较高,训练时间长,模型不易收敛,不宜在示功图识别中实际应用.
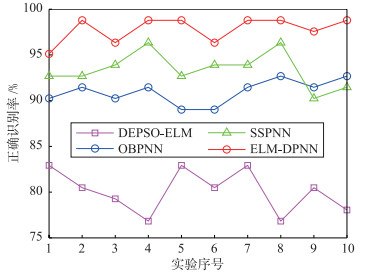
5.3 模型诊断对比分析针对82组示功图测试样本,4种模型的诊断误差对比情况如图 4和表 3所示,其中ELM-DPNN、OBPNN、SSPNN的诊断识别率均要高于DEPSO-ELM,并且ELM-DPNN效果最好,平均诊断识别率为97.804 87%,这在目前的示功图识别诊断上算是比较好的结果.
|
| 图 4 4种模型的识别率对比 Figure 4 Recognition rate comparison among four models |
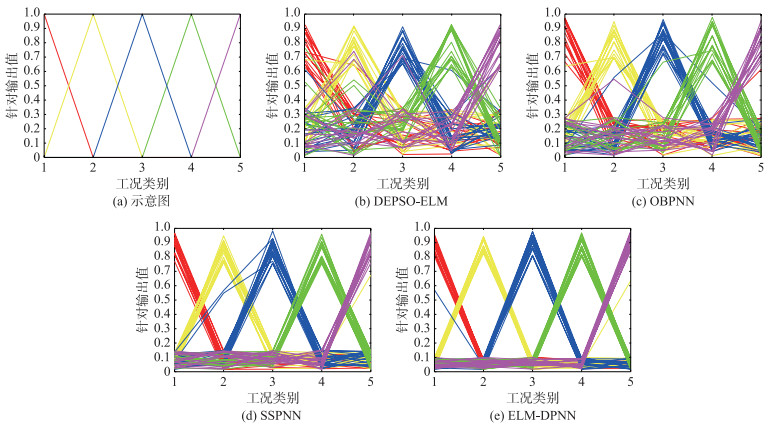
在示功图识别过程中,ELM-DPNN的对于每种工况的实际输出与表 1规定的期望输出之间最为接近,分类精度较高,而OBPNN和SSPNN距离期望输出稍远,分类精度略低,DEPSO-ELM分类精度最低.以ELM-DPNN和DEPSO-ELM为例进行说明,如对油杆断脱的测试样本,ELM-DPNN的诊断输出是(0.097 06,0.916 05,0.035 76,0.049 93,0.058 64),DEPSO-ELM的诊断输出是(0.231 35,0.681 34,0.453 79,0.120 93,0.155 48).假设模型实际输出若小于0.5,近似看作0;若大于0.5,则近似看作1,则二者均可正确完成示功图识别,但ELM-DPNN输出更接近于期望值,区分度更高,准确性更好.对于82组测试样本,为了更直观的进行说明诊断识别的对比情况,本文通过Matlab中的并行坐标系对测试样本集中的5种工况诊断结果进行同时显示,如图 5所示. 图 5(a)中横坐标的数字1、2、3、4、5分别代表正常、抽油杆断脱、固定凡尔漏失、双凡尔漏失和油杆偏磨这5种工况,纵坐标表示每种工况的期望输出值,例如固定凡尔漏失工况的期望输出值是(0,0,1,0,0),在图 5(a)中是第3个三角形,上顶点是1,代表诊断模型中为1的期望输出,其它4个在横轴上的点,代表诊断模型中为0的期望输出.若诊断模型对于样本的实际输出越接近于三角形的上顶点和横轴,诊断精度越好.若诊断模型对于样本的实际输出虽然接近上顶点,但是在距离横轴较远,则说明诊断的区分度有所降低.利用此种方法,对于82组测试样本,ELM-DPNN的每个三角形的顶点在分布上是最接近于1和横轴的0,SSPNN和OBPNN的分布性略差一些,而DEPSO-ELM最差.
|
| 图 5 诊断模型实际输出值分布 Figure 5 The output distribution of the diagnostic model |
模型诊断识别结果分析. DEPSO-ELM模型首先受同步瞬时输入限制,模型内部无法体现输入信号的时间累积效应,实际输出与期望输出之间误差较大,且区分度不高,故此模型诊断精度较低.此外输入和隐层的节点多,模型规模庞大,DEPSO优化算法染色体的维数高,很难收敛,因此在实际的示功图诊断中很难达到实用. OBPNN模型由于对离散过程输入首先要进行基函数拟合,然后对权函数进行基函数展开,根据基函数理论,理论上需要基函数项数为无穷多个,采用有限数目的正交基必然会影响模型精度. SSPNN虽然可以直接处理离散过程输入,内部通过使用样条函数,也仍具有PNN网络的时空聚合特性,但模型较为简单,可调参数较少,虽然计算效率高,但是却以牺牲逼近能力为代价. ELM-DPNN在内部数据机制上,直接对离散过程输入进行处理,内部通过三次样条数值积分来完成时空聚合运算,可以体现输入信号的时间累积效应,并且在离散输入数据序列首尾各补充了一个插值点,模型逼近能力相对于OBPNN和SSPNN略有增强,模型的实际输出与期望输出的误差较小,区分度高,所以诊断识别率高于其他两种PNN模型.
6 结论(1)本文针对示功图的识别诊断问题,为提高识别精度,提出一种ELM-DPNN模型,通过三次样条数值积分简化时间聚合运算,直接对离散过程输入进行处理.同时,为提高模型的训练速度,采用ELM进行训练,将网络学习转化为最小二乘问题,在计算出隐层输出矩阵后,通过使用Moore-Penrose广义逆和矩阵计算,通过隐层输出矩阵完成输出权值的求解,从而进行模型训练,学习速度有了一定提高.利用ELM-DPNN进行示功图识别时,直接将位移和载荷的离散数据序列作为模型输入,模型规模小,隐层时空聚合能力强,逼近能力较其它PNN模型有一定的提高.
(2)由于示功图采样数据不断更新,新的工况模式特征不断出现,如何在现有的ELM-DPNN诊断模型基础上,将不断获得的功图样本加入到诊断模型中,作为下一次工况诊断的已知信息,实现一种在线方式的ELM-DPNN示功图识别,是下一步的主要研究方向.此外对于ELM-DPNN中的随机参数和隐层过程神经元节点数可通过进化算法进行优化,提高模型收敛率,也是下一步的研究方向.
| [1] | 何岩峰, 吴晓东, 韩国庆. 示功图频谱分析新方法[J]. 石油学报 , 2008, 29 (4) : 619–624. He Y F, Wu X D, Han G Q. Frequency spectrum analysis method for recognition of dynamometer card[J]. Acta Petrolei Sinca , 2008, 29 (4) : 619–624. |
| [2] | Wu X D, Jiang H, Han G Q. Application of artificial neural network in indicator diagram[J]. Petroleum Science , 2004, 1 (1) : 27–35. |
| [3] | 徐芃, 徐士进, 尹宏伟. 有杆抽油系统故障诊断的人工神经网络方法[J]. 石油学报 , 2006, 27 (2) : 107–112. Xu L, Xu S J, Yin H W. Application of BP neural network and self-organizing competitive neural network to fault diagnosis of suck rod pumping system[J]. Acta Petrolei Sinca , 2006, 27 (2) : 107–112. |
| [4] | 任伟建, 王喜刚, 王思宇, 等. 基于模糊神经网络的抽油机故障诊断方法[J]. 自动化技术与应用 , 2012, 31 (4) : 4–9. Ren W J, Wang X G, Wang S Y, et al. Fault diagnosis method of pumping unit based on fuzzy neural network[J]. Techniques of Automation and Applications , 2012, 31 (4) : 4–9. |
| [5] | 何新贵, 梁久祯. 过程神经元网络的若干理论问题[J]. 中国工程科学 , 2000, 2 (12) : 40–44. He X G, Liang J Z. Some theoretical issues on procedure neural networks[J]. Engineering Science , 2000, 2 (12) : 40–44. |
| [6] | 许少华, 何新贵. 关于连续过程神经元网络的一些理论问题[J]. 电子学报 , 2006, 34 (10) : 1838–1842. Xu S H, He X G. Some theoretical issues on continuous process neural networks[J]. Acta Electronica Sinica , 2006, 34 (10) : 1838–1842. |
| [7] | 李洋, 钟诗胜. 多分辨小波过程神经网络及其应用研究[J]. 智能系统学报 , 2008, 3 (3) : 211–215. Li Y, Zhong S S. Research on multi-resolution wavelet process neural networks and applications[J]. CAAL Transactions on Intelligent Systems , 2008, 3 (3) : 211–215. |
| [8] | 李盼池, 王海英, 戴庆. 量子过程神经网络模型算法及应用[J]. 物理学报 , 2012, 61 (16) : 160303–1. Li P C, Wang H Y, Dai Q. Quantum process neural networks model algorithm and applications[J]. Acta Physica Sinica , 2012, 61 (16) : 160303–1. |
| [9] | 梁久祯. 分段式过程神经元网络[J]. 模式识别与人工智能 , 2006, 19 (3) : 295–299. |
| [10] | 刘志刚, 杜娟. 基于过程神经元网络的时间序列预测方法[J]. 计算机工程 , 2012, 38 (5) : 198–202. Liu Z G, Du J. Time series prediction method based on process neural networks[J]. Computer Engineering , 2012, 38 (5) : 198–202. |
| [11] | 王兵, 许少华. 基于半监督竞争学习过程神经网络的抽油机故障诊断[J]. 信息与控制 , 2014, 43 (2) : 235–240. Wang B, Xu S H. Fault diagnosis of pumping unit based on semi-supervised competitive learning process neural network[J]. Information and Control , 2014, 43 (2) : 235–240. |
| [12] | 钟诗胜, 雷达, 丁刚. 卷积和离散过程神经网络及其在航空发动机排气温度预测中的应用[J]. 航空学报 , 2012, 33 (3) : 438–443. Zhong S S, Lei D, Ding G. Convolution sum discrete process neural network and its application in aero engine exhausted gas temperature prediction[J]. Acta Aeronautica et Astronautica Sinica , 2012, 33 (3) : 438–443. |
| [13] | 许少华, 何新贵. 基于函数正交基展开的过程神经网络学习算法[J]. 计算机学报 , 2004, 27 (5) : 645–650. Xu S H, He X G. Learning Algorithms of process neural networks based on orthogonal function basis expansion[J]. Chinese Journal Of Computers , 2004, 27 (5) : 645–650. |
| [14] | Huang G B, Zhu Q Y, Siew C K. Extreme learning machine:A new learning scheme of feed forward neural networks[C]//Proceedings of International Joint Conference on Neural Networks(IJCNN2004). Piscataway, NJ, USA:IEEE, 2004:985-990. |
| [15] | Huang G B, Zhou H, Ding X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems Man & Cybernetics, Part B, Cybernetics:A Publication of the IEEE Systems Man & Cybernetics Society , 2012, 42 (42) : 513–29. |
| [16] | Kasun L L C, Zhou H, Huang G B, et al. Representational learning with ELMs for big data[J]. IEEE Intelligent Systems , 2013, 28 (6) : 31–34. |
| [17] | 遇炳杰. 加权极限学习机在变压器故障诊断中的应用[J]. 计算机工程与设计 , 2013, 34 (12) : 4340–4344. Yu B J. Transformer fault diagnosis using weighted extreme learning machine[J]. Computer Engineering and Design , 2013, 34 (12) : 4340–4344. |
| [18] | 林海金, 罗飞, 苏彩虹. 一种新的混合智能学习机[J]. 控制与决策 , 2015, 30 (6) : 1078–1084. Lin H J, Luo F, Su C H. An improved hybrid intelligent extreme learning machine[J]. Control and Decision , 2015, 30 (6) : 1078–1084. |
| [19] | 孙毅刚, 刘静雅, 赵珍. 基于极限学习机的航空发动机传感器故障诊断[J]. 传感器与微系统 , 2014, 33 (8) : 23–26. Sun Y G, Liu J Y, Zhao Z. Aircraft engine sensor fault diagnosis based on extreme learning machine[J]. Transducer and Microsystem Technology , 2014, 33 (8) : 23–26. |
| [20] | 王超, 王建辉. 改进式混合增量极限学习机算法[J]. 控制与决策 , 2015, 30 (11) : 1982–1985. Wang C, Wang J H. Improved hybrid incremental extreme learning machine algorithm[J]. Control and Decision , 2015, 30 (11) : 1982–1985. |
| [21] | 李盼池, 王海英. 基于样条插值函数的离散过程神经网络训练[J]. 计算机应用研究 , 2011, 28 (1) : 75–81. Li P C, Wang H Y. Discrete process neural networks training based on spline function[J]. Application Research of Computers , 2011, 28 (1) : 75–81. |



