2. 福建江夏学院电子信息科学学院, 福州 福建 350108 ;
3. 福州大学数学与计算机科学学院, 福州 福建 350116
2. College of Electronics and Information Science, Fujian Jiangxia University, Fuzhou 350108, China ;
3. College of Mathematics and Computer Science, Fuzhou University, Fuzhou 350116, China
1 引言
近年来,突发事件频频发生,给国家和社会带来了严重的生命财产损失,因此,应急管理引起了国内外学者的关注.应急决策是应急管理的重要研究内容之一,许多学者通过决策方法寻求最优的应急方案来降低损失、控制事态的发展.常用的决策方法有前景理论[1]、案例推理[2]、博弈论[3]、群决策[4]等,其中案例推理可以根据历史经验快速生成应急方案,符合人的思维方式[5],受到广泛的青睐,比如,Fan等[2]针对突发事件中的5种数据类型提出相似度计算方法来解决基于案例推理的应急方案生成问题,随后在文[6]中应用案例推理对中国某个城市的地铁项目应急响应进行实证研究.李永海等[7]提出了在无法确定各自然状态情景下运用案例推理进行应急方案选择的方法.郑晶等[8]提出一种基于证据推理的考虑总体优势度的应急方案生成方法.
上述研究中,案例推理在相似度计算方面的研究已经很成熟,但最相似历史案例的方案在大多情况下需要进行调整才能应用于当前突发事件中,因此如何对案例进行调整引起了国内外学者的关注.以往案例调整大多根据决策者的专业知识和经验进行调整[9],这对专业性要求较高.目前很多学者开始对方案如何自动调整进行研究,比如,基于距离[10]或者相似度值[11]的统计型案例调整方法,虽然应用简单,但是准确性较低[12].为了提高调整的精确度,Qi等[13]在基于相似度的统计方法中融入调整值来提高调整能力. Hu等[14]引入相似度和灰色关联度混合的方式来确定权重以此提高案例调整方法的精确性.另外一些学者是通过引入机器学习方法来提高精确度,例如,Liao等[15]应用改进的遗传算法学习目标案例与相似案例之间方案的差异来获得目标案例的解决方案. Butdee等[16]提出应用神经网络进行案例调整. Qi等在文[13]的基础上提出利用支持向量机方法学习问题与方案之间的函数关系来进行案例调整[17],更进一步提高了案例调整性能.机器学习方法虽然能够提高精确度,但需要大量的数据和付出高昂的计算代价.同时,神经网络、支持向量机方法和遗传算法均是黑箱的学习过程且需要指定特定的函数.特别需要指出的是,目前的调整方法都只针对数值型数据进行调整.
已有的研究为案例调整提供了理论与方法上的借鉴与指导.但突发事件具有突发性、随机性等特点且存在信息不确定性,目前的调整方法无法解决模糊数的调整问题.鉴于此,本文引入置信规则库进行案例调整.置信规则库方法不仅可以处理不确定的数据,而且是一个白箱学习过程.因此,基于规则库的应急方案调整方法的研究具有重要的理论和实际意义.
2 置信规则库推理方法Yang等[18]于2006年在证据推理、决策理论、模糊理论和传统IF-THEN规则库的基础上提出了基于证据推理算法的置信规则库推理方法(belief Rule-base Inference Methodology using the Evidential Reasoning approach,RIMER). RIMER能够处理不确定性、不完整等信息,因此在不确定多属性决策问题中受到广泛青睐. RIMER包括两个方面:一是知识表示,这里主要通过置信规则库(belief rule base,BRB)系统来实现;二是推理机制,这主要通过证据推理(evidential reasoning,ER)算法来实现.下面给出简要的介绍.
2.1 基于BRB的知识表示BRB是由一系列置信规则构成的,假设BRB中共有M个前提属性,则第k条置信规则的描述如下:
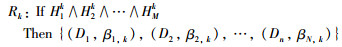
|
(1) |
其中,Hik(i=1,2,…,M,k=1,2,…,L)表示第k条规则中第i个前提属性的评价等级;M表示第k条规则中前提属性的数目;L表示BRB系统中的规则数目;βj,k(j=1,2,…,N)表示在第k条规则结论中关于评价等级Dj的置信度;如果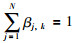
此外,第k条规则还包含规则权重θk(k=1,2,…,L)和前提属性权重δi,k(i=1,2,…,M),分别表示了第k条规则相对于其它规则的重要性和在第k条规则中第i个前提属性相对于其它前提属性的重要性.
2.2 基于BRB的推理机制基于BRB的推理机制包括激活权重计算和激活规则合成两个步骤.
2.2.1 激活权重计算假设输入信息x=(x1,x2,…,xM),其中xi(i=1,2,…,M)表示输入信息的第i个前提属性,根据文[17]的信息转换技术,将xi转换为等级分布式评价形式S(xi)={(Hi,j,αi,j)}:
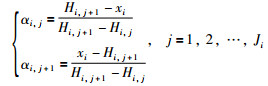
|
(2) |
其中,Hi,j表示第i个前提属性的第j个评价等级;αi,j表示xi在评价等级Hi,j上的置信度,αi,j≥0,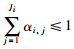
然后,结合属性权重和规则权重θk计算第k条规则的激活权重:
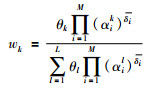
|
(3) |
其中,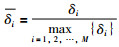
激活规则合成主要是应用ER来实现. ER主要分为2个步骤:一是,将输出部分的置信度转换为基本信度分布[19-20],转换公式如下:
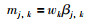
|
(4) |
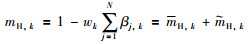
|
(5) |
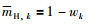
|
(6) |
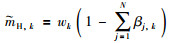
|
(7) |
然后,利用ER的解析法[21]将所有的基本属性进行合成,合成公式为
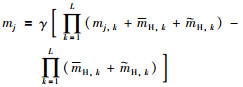
|
(8) |
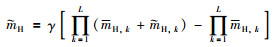
|
(9) |
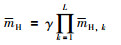
|
(10) |
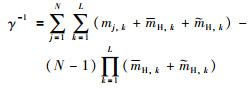
|
(11) |
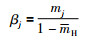
|
(12) |
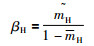
|
(13) |
其中,βj表示评价等级Dj的置信度,βH表示不完整信息的置信度.
最后,通过效用将置信度结构转换为数值.设在评价等级Dj上的效用值为μ(Dj)(j=1,2,…,N),则输出结果表示为
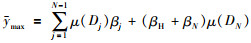
|
(14) |
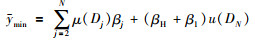
|
(15) |
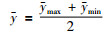
|
(16) |
本文中案例采用二元组形式表示,即案例=(问题,方案).设Z={(P1,S1),(P2,S2),…,(Pq,Sq)}表示q个历史案例构成的历史案例集,其中Pr表示第r个历史案例的问题,Sr表示第r个历史案例的方案,r=1,2,…,q;P0表示目标案例的问题,S0为目标案例要生成的方案. CP={C1P,C2P,…,CaP}表示问题的属性集,其中CeP表示第e个属性,e=1,2,…,a;xr=(xr1,xr2,…,xra)表示问题Pr的属性值向量,其中xre表示问题Pr的第e个属性;wP=(w1P,w2P,…,waP)表示问题的属性权重向量,其中weP表示属性CeP的权重,满足weP≥0且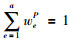
案例推理是通过某种检索方法从历史案例库中搜到与目标案例最相似的历史案例,然后通过重用或修改最相似历史案例的方案来获取目标案例的解决方案.其中案例调整的步骤需要根据历史案例中问题Pr和方案Sr的信息来获取问题与方案之间的关系,进而由目标案例的问题P0计算得到目标案例的方案S0.基于置信规则库的调整方法,通过学习问题Pr和方案Sr之间的因果关系来确定置信规则库,在此基础上,利用BRB的推理机制获取目标问题的方案S0.
本文要解决的问题是,针对当前要解决的问题P0,根据历史案例集Z及问题属性权重wP,如何运用一个可行的决策分析方法来调整与P0最相似案例的方案,以此得到当前突发事件的有效方案.
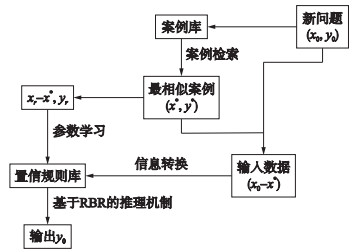
3.2 基于置信规则库的调整方法 3.2.1 案例调整框架为了生成目标案例的有效方案,这里提出一种基于置信规则库的调整方法.参考Policastro等[22]提出的案例调整模型,图 1展示了基于置信规则库的方案调整框架(ABRB).首先,检索出与目标案例最相似的历史案例;然后,根据最相似案例与历史案例的信息,学习得到案例规则库;最后,利用目标案例与最相似历史案例的问题差异来激发规则进行推理,得到目标案例的解决方方案.
|
| 图 1 基于置信规则库的方案调整框架 Figure 1 The alternative adaptation framework based on belief rule base |
突发事件具有不确定性等特点,表示案例的属性数据类型也存在多样化.针对不同属性类型的案例相似度计算,文[2]做了较为详细的研究.本文只考虑数值型的问题属性,首先,计算案例属性距离d(x0e,xre),计算公式如下:
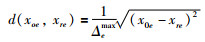
|
(17) |
其中,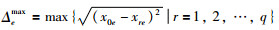
进一步地,计算目标案例与历史案例关于问题的属性相似度S(x0e,xre),计算公式如下:
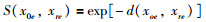
|
(18) |
最后,计算目标案例与历史案例关于问题的相似度S(x0,xr),计算公式如下:
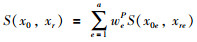
|
(19) |
其中,S(x0,xr)∈[0, 1].显然,S(x0,xr)越大,表明历史案例与目标案例的问题相似度越高.选择S(x0,xr)值最大的案例作为最相似的历史案例(P*,S*),相应的问题属性向量为x*=(x1*,x2*,…,xa*),相应的方案属性向量为y*=(y1*,y2*,…,yb*).
3.2.3 案例规则库的学习置信规则库系统中的参数(θk,δi,βj,k)通常由专家根据自身的经验和历史信息给定的,反映专家对研究对象的认知程度.然而,由于专家自身认知的局限性,往往难以反映系统的行为,导致系统推理性不高,因此,Yang等很早就在文[18]中提出需要通过参数学习来改善系统的推理能力.本文采用的参数学习方法的思想是根据历史案例库中的信息,利用优化模型对专家给定的初始BRB系统的参数进行训练,使训练后的系统能很好地反映案例库的行为.下面给出案例规则库参数学习的步骤.
首先,计算最相似历史案例与其他历史案例关于问题的差异值Δxre,计算公式如下:
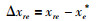
|
(20) |
然后,设置置信规则库前提和结论属性的评价等级,并初始化置信规则库.设前提属性的评价等级分为{H1,H2,H3}三个等级,表示问题属性的差异值为低(low)、中(medium)、高(high),令H1=min{Δxre},H3=max{Δxre},H2=(H1+H3)/2.结论属性的评价等级也分为{D1,D2,D3}三个等级,例如,针对方案属性“出动的救援力量”表示出动救援力量的少(low)、中(medium)、多(high),令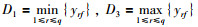
在此基础上,根据式(2)将Δxre转换为置信度规则形式,并作为置信规则库的前提条件,利用基于BRB的推理机制得到输出结果yr.学习模型主要通过不断调整置信规则库中的参数(θk,δi,βj,k)使得yr与yr之间的差距达到一定的阈值,参考Wang在文[23]提出的学习模型,创建学习模型如下:
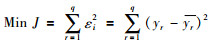
|
(21) |
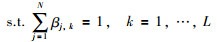
|
(22) |
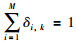
|
(23) |
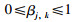
|
(24) |
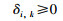
|
(25) |
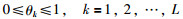
|
(26) |
其中,式(21)为目标函数,其含义是最小化预测输出与实际输出之间的差异;式(22)和式(24)是每条置信规则的后件置信度的限制;式(23)和式(25)是属性权重的限制;式(26)是规则权重的限制.
3.2.4 获取目标案例的解在上述学习得到案例规则库基础上,通过基于BRB的推理机制可以得到目标案例的解,其具体步骤如下:
首先,根据式(20)计算目标案例与最相似案例关于问题的差异Δxoe=xoe-xe*.
然后,根据式(2)将Δxoe转换为等级分布式评价形式S(xi)={(Hi,j,αi,j)}.
进一步,根据式(3)计算激活权重wk.
最后,根据式(4)~(13)对激活的规则进行融合得到结论置信度{β1,β2,…,βN}.若结果为区间数,根据式(14)、式(15)得到结果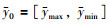
考虑一个液体泄漏应急方案生成问题.当某地区发生液体泄漏时,需要采取有效的应急方案进行响应.当前案例库中有30个同类型的历史案例((P1,S1),(P2,S2),…,(P30,S30)).案例的问题属性包括:泄漏量(C1P,单位:t),泄漏强度(C2P,单位:kg/s),存储总量(CP3,单位:吨)和人口规模(CP4).方案属性为出动的救援力量(C1S,单位:人),其数据类型为区间数.问题属性权重wp=(0.269 3,0.249 0,0.259 2,0.222 4).计算过程中,选择案例(P30,S30)作为目标案例,其它29个案例作为历史案例.案例信息如表 1所示.为了说明本文方法的可行性,下面给出计算过程.
| 案例 | C1P | C2P | CP3 | CP4 | C1S |
| (P1,S1) | 3 000 | 0.6 | 12 | 4 200 | [68, 72] |
| (P2,S2) | 3 000 | 1.2 | 10 | 4 000 | [80, 82] |
| (P3,S3) | 2 300 | 0.8 | 8 | 3 200 | [65, 67] |
| (P4,S4) | 4 000 | 1.5 | 11 | 3 000 | [80, 85] |
| (P5,S5) | 1 800 | 0.7 | 18 | 2 800 | [60, 63] |
| (P6,S6) | 3 800 | 2 | 20 | 2 500 | [87, 90] |
| (P7,S7) | 1 500 | 0.5 | 9 | 2 750 | [58, 61] |
| (P8,S8) | 4 380 | 1.9 | 23 | 3 600 | [100, 105] |
| (P9,S9) | 2 800 | 1.5 | 15 | 1 700 | [67, 70] |
| (P10,S10) | 2 500 | 1.8 | 12 | 2 600 | [71, 73] |
| (P11,S11) | 1 200 | 0.4 | 9 | 2 000 | [50, 53] |
| (P12,S12) | 4 580 | 1.7 | 15 | 3 100 | [83, 87] |
| (P13,S13) | 4 780 | 1.2 | 13 | 2 300 | [77, 81] |
| (P14,S14) | 4 300 | 1.65 | 17 | 3 800 | [87, 89] |
| (P15,S15) | 3 300 | 0.5 | 10 | 3 800 | [63, 65] |
| (P16,S16) | 3 500 | 0.8 | 10 | 4 000 | [75, 77] |
| (P17,S17) | 2 750 | 1.1 | 11 | 3 800 | [70, 75] |
| (P18,S18) | 3 600 | 1 | 15 | 4 100 | [80, 83] |
| (P19,S19) | 3 750 | 0.9 | 11 | 3 900 | [76, 79] |
| (P20,S20) | 3 200 | 0.7 | 9 | 3 600 | [67, 71] |
| (P21,S21) | 2 900 | 0.75 | 13 | 3 900 | [69, 70] |
| (P22,S22) | 2 850 | 1.1 | 17 | 3 750 | [63, 65] |
| (P23,S23) | 2 000 | 1.3 | 13 | 3 500 | 70 |
| (P24,S24) | 4 100 | 0.8 | 10 | 3 300 | [84, 85] |
| (P25,S25) | 4 050 | 0.9 | 15 | 3 000 | [81, 83] |
| (P26,S26) | 3 300 | 1 | 11 | 3 800 | [69, 73] |
| (P27,S27) | 3 300 | 0.7 | 12 | 4 000 | [72, 75] |
| (P28,S28) | 3 500 | 1.3 | 12 | 3 900 | [74, 75] |
| (P29,S29) | 2 900 | 0.7 | 9 | 2 300 | [65, 67] |
| (P30,S30) | 3 200 | 0.8 | 10 | 4 000 | [70, 75] |
首先,依据式(17)~(19),计算目标案例(P30,S30)与历史案例(Pr,Sr)之间的问题相似度S(x30,xr),得到与之最相似的历史案例为(P16,S16).
其次,根据式(20)计算历史案例(Pr,Sr)与案例(P16,S16)的问题属性差值Δxre,进而给出问题属性差异及其方案属性的评价等级,如表 2所示.
| Low | Medium | High | |
| 泄漏量/kg | -2 300 | -510 | 1 280 |
| 泄漏强度/(kg/s) | -0.4 | 0.4 | 1.2 |
| 存储总量/吨 | -2 | 5.5 | 13 |
| 人口规模 | -2 300 | -1 050 | 200 |
| 出动的救援力量 | 50 | 77.5 | 105 |
然后,将问题属性差值Δxre依据表 2和式(2)转换成评价等级置信度形式S(xi)={(Hi,j,αi,j)};
接下来,调用案例规则库的学习方法来确定BRB的参数(θk,δi,βj,k),以此得到学习后的置信规则库.
进一步地,把案例(P30,S30)的问题属性作为输入数据,依据式(20)计算案例(P30,S30)与(P16,S16)之间的差异Δx30e,并依据式(2)转换成置信度形式;
最后,根据式(4)~(16),调用BRB推理机制,得到(P30,S30)的解决方案为[71.8,75.4].
从上述结果来看,案例(P30,S30)实际采用的方案为[70, 75],通过基于置信规则库的应急方案调整方法得到的方案为[71.8,75.4].若没有考虑对相似案例的方案进行调整,将采用相似度最大的历史案例的方案作为当前应急方案,即采用历史案例(P16,S16)的方案[75, 77].为了能更好地定量分析调整得到的结果的准确性,根据区间数的欧氏距离,得到案例(P16,S16)的方案与实际方案之间的距离为5.385 2,由本文提出方法得到的方案值与实际方案之间的距离为1.843 9.本文提出方法得到的方案值与实际值的距离比案例(P16,S16)的方案小,因此本文提出的方法得到的方案比未调整之前的方案更接近实际值.本算例中,解决方案的含义为出动的救援力量,那么历史案例(P16,S16)的方案值为[75, 77],即例(P16,S16)派出的最少救援力量为75人;实际方案值为[70, 75],即实际最多才派出75人,因此,若采用历史案例(P16,S16)的方案将增加一定的应急成本.
4.2 性能比较为了说明本文方法的有效性,下面给出本文方法与其他方法的性能比较.
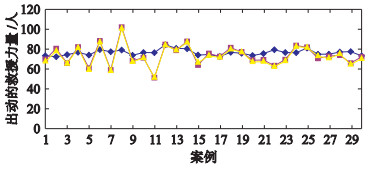
首先,为验证通过参数学习能够提高决策性能的有效性,将初始化BRB系统得到各案例的方案、学习参数后的BRB系统得到各案例的方案与各案例的实际方案进行比较,其结果如图 2所示.
|
| 图 2 BRB系统得到的方案与实际方案的比较 Figure 2 Comparison between the predictive and the actual alternative of BRB system |
图 2中,初始BRB系统得到的方案并不能准确地拟合实际方案,因此需要对初始的BRB系统进行参数训练.定量分析初始化和学习后的方案值与实际值之间的均方差(mean squared error,MSE),其中初始化的MSE为92.565 8,而使用训练后的MSE为1.569 5,相对缩小了98.3%.因此,参数通过训练后能更好地拟合实际值.
进一步,将本文提出方法与经典调整方法,如基于逆距离加权平均(inverse distance weighted mean,IDWM)和基于相似度倒数(reciprocal of similarity,RS)的调整方法、基于神经网络的调整方法,及其文[14]提出方法进行比较.其中距离采用的是曼哈顿距离,相似度分别采用了比率函数[24]和距离函数[25].由于经典方法只能处理数值型数据,因此将表 1中的解决方案的值取中间值,即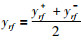
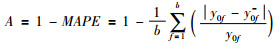
|
(27) |
式中,y0j是案例(P0,S0)关于方案属性j的精确值,y0j-为调整值,N是解的属性数量.计算上述几种方法调整后的精确度,结果如表 3所示.由于突发事件数据的匮乏,本文把学习数据也作为测试数据.
| HGS | BRBA | RRS | ID | DRS | NN | |
| C21 | 0.941 5 | 0.992 8 | 0.941 4 | 0.933 2 | 0.940 9 | 0.979 0 |
| C22 | 0.858 5 | 0.998 4 | 0.857 0 | 0.855 0 | 0.857 1 | 0.986 7 |
| C23 | 0.941 4 | 0.992 8 | 0.946 3 | 0.911 2 | 0.945 1 | 0.991 2 |
| C24 | 0.863 2 | 0.996 4 | 0.852 7 | 0.784 0 | 0.853 7 | 0.999 3 |
| C25 | 0.901 5 | 0.991 4 | 0.894 5 | 0.828 6 | 0.894 5 | 0.995 7 |
| C26 | 0.958 2 | 0.956 9 | 0.958 8 | 0.977 7 | 0.958 4 | 0.881 3 |
| C27 | 0.994 6 | 0.993 2 | 0.996 5 | 0.987 0 | 0.996 0 | 0.984 2 |
| C28 | 0.999 7 | 0.980 3 | 0.999 5 | 0.958 5 | 0.998 0 | 0.834 2 |
| C29 | 0.902 4 | 0.997 0 | 0.901 3 | 0.879 2 | 0.900 1 | 0.999 4 |
| C30 | 0.982 3 | 0.997 2 | 0.983 5 | 0.992 6 | 0.983 1 | 0.993 4 |
由表 3可知,本文提出的方法在案例(C21,C22,C23,C24,C25,C27,C29,C30)上的精确度大部分高于其它方法的精确度,且接近于1,只有在案例C26上的精确度比HGS低0.001 3、比RRS低0.001 9、比ID低0.020 8、比DRS低0.001 5,在案例C28上的精确度比HGS低0.019 4、比RRS低0.019 2,比DRS低0.017 7,在案例C24上的精确度比NN低0.002 9,在案例C25上的精确度比NN低0.004 3,在案例C29上的精确度比于NN低0.002 4.
最后,通过平均调整精度说明本文提出方法的有效性.平均调整精确度计算公式为
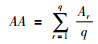
|
(28) |
根据式(28)计算案例集(C21,C22,…,C30)进行案例调整后的平均精确度.本文提出方法的平均精确度为:0.989 4,HGS方法的平均精确度为0.932 5,RRS方法的平均精确度为0.931 7,ID方法的平均精确度为0.911 7,DRS方法的平均精确度为0.931 2,NN方法的平均精确度为0.959 6.本文方法比HGS方法相对提高了5.75%,比RRS方法相对提高了5.83%,比ID方法相对提高了7.85%,比DRS方法相对提高了5.89%,比NN方法提高了3.012 9%.
综上所述,通过与经典的案例调整方法和文[14]的调整方法对比,本文提出的应用学习后的置信规则库对数值型方案进行调整方法可以调高预测方法的精确度.
5 结束语置信规则库不仅可以处理不确定数据问题,而且该方法是一个白箱的学习过程,便于融入决策者的偏好.因此,本文在应用案例推理生成应急方案的方案调整步骤中,引入置信规则库学习问题与方案之间的关系,以此获得目标案例更有效的方案.基于置信规则库的应急方案调整方法,不仅解决了案例调整中存在不确定数据的问题,而且可以生成对目标案例更有效的应急方案.在算例分析中,不仅分析了该方法的可行性,同时通过分析实际值与调整值之间的关系及调整的平均精确度说明了该方法的有效性.对于今后的研究,将进一步探索更有效的案例调整方法.
| [1] | Liu Y, Fan Z P, Zhang Y. Risk decision analysis in emergency response:A method based on cumulative prospect theory[J]. Computers & Operations Research , 2014, 42 (2) : 75–82. |
| [2] | Fan Z P, Li Y H, Wang X, et al. Hybrid similarity measure for case retrieval in CBR and its application to emergency response towards gas explosion[J]. Expert Systems with Applications , 2014, 41 (5) : 2526–2534. DOI:10.1016/j.eswa.2013.09.051 |
| [3] | Yang J, Xu C. Emergency decision engineering model based on sequential games[J]. Systems Engineering Procedia , 2012, 5 : 276–282. DOI:10.1016/j.sepro.2012.04.043 |
| [4] | 张云龙, 刘茂, 李剑峰. 模糊群体决策方法在应急决策中的应用[J]. 中国安全科学学报 , 2009, 19 (2) : 33–37. Zhang Y L, Liu M, Li J F. The application of fuzzy group decision method to the decision-making of emergency[J]. China Safety Science Journal , 2009, 19 (2) : 33–37. |
| [5] | 严爱军, 于远航. 基于案例推理的PID控制器参数认知整定方法[J]. 信息与控制 , 2015, 44 (5) : 525–530. Yan A J, Yu Y H. Cognitive tuning method based on case-based reasoning for PID controller's parameters[J]. Information and Control , 2015, 44 (5) : 525–530. |
| [6] | Fan Z P, Li Y H, Zhang Y. Generating project risk response strategies based on CBR:A case study[J]. Expert Systems with Applications , 2015, 42 (6) : 2870–2883. DOI:10.1016/j.eswa.2014.11.034 |
| [7] | 李永海, 樊治平, 李铭洋. 解决广义不确定型决策问题的案例决策方法[J]. 系统工程学报 , 2012, 29 (1) : 21–29. Li Y H, Fan Z P, Li M Y. Case-based decision analysis method for general uncertain decision making problem[J]. Journal of Systems Engineering , 2012, 29 (1) : 21–29. |
| [8] | 郑晶, 王应明, 叶歆. 考虑应急方案总体优势度的决策方法[J]. 控制与决策 , 2014, 30 (7) : 1239–1244. Zheng J, Wang Y M, Ye X. A decision method for emergency alternative with considering total superiority degree[J]. Control and decision , 2014, 30 (7) : 1239–1244. |
| [9] | Smyth B, Keane M T. Using adaptation knowledge to retrieve and adapt design cases[J]. Knowledge-based systems , 1996, 9 (2) : 127–135. DOI:10.1016/0950-7051(95)01024-6 |
| [10] | Li S T, Ho H F. Predicting financial activity with evolutionary fuzzy case-based reasoning[J]. Expert Systems with Applications , 2009, 36 (1) : 411–422. DOI:10.1016/j.eswa.2007.09.049 |
| [11] | Yu W D, Liu Y C. Hybridization of CBR and numeric soft computing techniques for mining of scarce construction databases[J]. Automation in Construction , 2006, 15 (1) : 33–46. DOI:10.1016/j.autcon.2005.01.007 |
| [12] | Tonidandel F, Rillo M. Case adaptation by segment replanning for case-based planning systems[M]. Berlin, Germany: Springer , 2005 : 579 -594. |
| [13] | Qi J, Hu J, Peng Y. A new adaptation method based on adaptability under k-nearest neighbors for case adaptation in case-based design[J]. Expert Systems with Applications , 2012, 39 (7) : 6485–6502. DOI:10.1016/j.eswa.2011.12.055 |
| [14] | Hu J, Qi J, Peng Y. New CBR adaptation method combining with problem-solution relational analysis for mechanical design[J]. Computers in Industry , 2015, 66 (1) : 41–51. |
| [15] | Liao Z, Mao X, Hannam P M, et al. Adaptation methodology of CBR for environmental emergency preparedness system based on an Improved Genetic Algorithm[J]. Expert Systems with Applications , 2012, 39 (8) : 7029–7040. DOI:10.1016/j.eswa.2012.01.044 |
| [16] | Butdee S. Adaptive aluminum extrusion die design using case-based reasoning and artificial neural networks[M]. Berlin, Germany: Springer , 2012 : 6747 -6754. |
| [17] | Qi J, Hu J, Peng Y. Incorporating adaptability-related knowledge into support vector machine for case-based design adaptation[J]. Engineering Applications of Artificial Intelligence , 2015, 37 (1) : 170–180. |
| [18] | Yang J B, Liu J, Wang J, et al. Belief rule-base inference methodology using the evidential reasoning approach-RIMER[J]. IEEE Transactions on Systems, Man and Cybernetics, Part A:Systems and Humans , 2006, 36 (2) : 266–285. DOI:10.1109/TSMCA.2005.851270 |
| [19] | Wang Y M, Yang J B, Xu D L. Environmental impact assessment using the evidential reasoning approach[J]. European Journal of Operational Research , 2006, 174 (3) : 1885–1913. DOI:10.1016/j.ejor.2004.09.059 |
| [20] | 段新生. 证据理论与决策、人工智能[M]. 中国人民大学出版社 ,1993 . Duan X S. Evidence theory and decisions, artificial intelligence[M]. China Renmin University Press , 1993 . |
| [21] | Wang Y M, Yang J B, Xu D L, et al. The evidential reasoning approach for multiple attribute decision analysis using interval belief degrees[J]. European Journal of Operational Research , 2006, 175 (1) : 35–66. DOI:10.1016/j.ejor.2005.03.034 |
| [22] | Policastro C A, Carvalho A C, Delbem A C B. A hybrid case adaptation approach for case-based reasoning[J]. Applied Intelligence , 2008, 28 (2) : 101–119. DOI:10.1007/s10489-007-0044-4 |
| [23] | Wang Y M, Yang J B, Xu D L, et al. Consumer preference prediction by using a hybrid evidential reasoning and belief rule-based methodology[J]. Expert Systems with Applications , 2009, 36 (4) : 8421–8430. DOI:10.1016/j.eswa.2008.10.052 |
| [24] | Chou J S. Web-based CBR system applied to early cost budgeting for pavement maintenance project[J]. Expert Systems with Applications , 2009, 36 (2) : 2947–2960. DOI:10.1016/j.eswa.2008.01.025 |
| [25] | Zhang S. Nearest neighbor selection for iteratively kNN imputation[J]. Journal of Systems and Software , 2012, 85 (11) : 2541–2552. DOI:10.1016/j.jss.2012.05.073 |



