2. 江南大学轻工过程先进控制教育部重点实验室, 江苏 无锡 214122
2. Key Laboratory of Advanced Process Control for Light Industry(Ministry of Education), Jiangnan University, Wuxi 214122, China
1 引言
在实际工业生产过程控制中,需要对一些关键变量进行严格的把关,以满足一系列质量控制要求,在现有的技术条件及经济代价等问题的制约下直接获取关键变量十分困难.因此,软测量技术应运而生[1-5],它通过构造过程易测变量与难测变量之间的数学关系来推断和估计待测主导变量,用软件的方式进行“测量”.传统的软测量建模方法大多考虑零时延特性,即考虑输入输出具有同样的采样间隔且在数据库中按时刻一一对应.然而,通过各个传感器采集的输入数据及通过实验室分析或者在线仪表获得的输出数据间往往存在着显著的时间滞后,如果继续采用稳态情况下的建模方法,建立的模型已经不能完全解释过程的特性.为了确保软测量模型能够在较长时间内实现关键变量的精确预测,有必要采取措施引入过程的时滞动态信息.
关于过程时滞信息的估计研究,Fortuna[6]等利用过程装置的工艺设计参数估计装置时延的大概范围,但是估计精度较低; Komulainen[7]和Zhang[8]通过计算输入输出变量的相关系数来估计时延,但是对于非线性过程效果不佳.阮宏镁[9]等运用DE(difference estimation)算法优化脱丁烷塔过程变量间的联合互信息来确定过程时滞参数,但是智能优化算法往往会陷入局部最优,且近邻互信息分析相关性时计算复杂度较高,很难在短时间内获得一个可靠的解集.
本质上来说,无论是互信息方法还是其它估计时延的方法,大多都在寻找与主导变量最密切相关的辅助变量用于建模.当投入实际应用中时,需要在算法复杂度与算法精度上取得折中.针对时延估计问题,本文将采用模糊曲线分析(fuzzy curve analysis,FCA)的方法将变量时滞信息引入到软测量模型中.模糊曲线方法最早由Lin[10]提出并用于简化模糊规则,确定模糊神经网络模型结构,而后文[11]将模糊曲线方法用于过失误差数据的检测中.这种方法的特点是计算复杂度较低同时易于理解,能够直观有效地确定输入变量的重要性程度.
为了对过程动态实时有效地进行跟踪和控制,软测量模型性能可以通过周期性地重建来维护,主要方法包括MW(moving-window)方法[12-13]、 迭代方法[14]和JIT(just-in-time)方法[15-16],但这些方法往往需要频繁更新模型,而时间差(time difference,TD)模型能够处理随时间推移造成的模型性能下降,使得重建模型的可能性最小化[17-19].
兼顾工业过程中的时滞特性及对过程动态的在线跟踪,本文将以离线方式确定各变量时滞,然后于在线阶段建立时间差软测量模型.首先通过FCA方法,充分挖掘出历史数据库所包含的信息,用离线条件下得到的时滞参数对软测量建模数据进行重构; 然后,对于新到来的样本数据,基于时间差—高斯过程回归(time difference Gaussian process regression,TDGPR)模型进行不同时间差条件下的在线预测.通过实际工业脱丁烷塔过程塔底丁烷浓度的软测量建模仿真实验,验证了所提FCA-TDGPR方法的有效性.
2 问题描述传统不考虑过程时滞方法的软测量建模数据为{X(t),y(t)},t=1,2,…,N,N为样本数,t时刻的输入表示为X(t)=[x1(t),x2(t),…,xm(t)]T,m为输入样本的维数,X(t)∈Rm,y(t)∈R.由过程机理可知,不同的辅助变量有着不同的延迟时间,与y(t)相关的并不是t时刻测得的输入X(t),而是di时刻(定义为输入变量xi的最优时滞参数)之前的历史输入.若不考虑时滞问题,则辅助变量与主导变量间实际的因果关系被打乱,因此需要估计出各辅助变量与主导变量间的时滞,得到“重构变量输入”来代替原数据库中的“实时输入”进行建模,重构输入如式(1)所示,重构的建模数据为
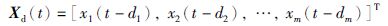
|
(1) |
实际过程的延迟时间通常不会无穷大,可以根据过程的机理或先验知识得到,本文假定各变量存在的最大延迟参数为Tmax,有0≤di≤Tmax,di∈N.
通过上述思路将原过程不含时滞的m维: “实时输入变量集”以式(2)方式对每个变量分别扩展,共获得m·(Tmax+1)维“时滞输入变量集”用以分析和建模.

|
(2) |
对于xi(t)对应的Tmax+1维扩展变量集,确定最优的时滞参数di,是本文需要解决的主要问题.
本文将从分析辅助变量与主导变量间的相关性出发,采用模糊曲线方法估计过程各辅助变量时延值,并用于样本重构和软测量在线预测.
3 含变量时滞估计的TDGPR方法 3.1 基于模糊曲线的变量时滞估计在软测量建模过程中,需要选取最有效的变量来建立可靠的模型,以充分描述过程的动态特性.假设有输入变量集{xi,i=1,2,…,m}及输出变量y,对于输入变量xi,t时刻采集的样本值记作xi(t),对于(xi(t),y(t)),输入变量xi的模糊隶属度函数定义为

|
(3) |
对于每一个xi,{Φit,y(t)}提供了一条模糊规则,描述为{if xi is Φit(xi),then y is y(t)},Φit为变量xi关于第t个数据点的输入变量模糊隶属度函数,式(3)选取的是高斯模糊隶属度函数,b取变量xi值域范围的20%.故N个训练样本对应每个变量都有N条模糊规则.在模糊隶属度函数中,每个点对应的{xi(t),y(t)}处,有Φit=1.
对于时延过程,通过引入时滞信息,原变量xi变为Tmax+1维,可表示为xi(t-λ),λ=0,1,…,Tmax,λ为引入的变量时延值.通过式(4)对扩展后的每个新变量质心去模糊化,可得到第i个变量时延值为λ条件下的模糊曲线Ci,λ.如式(5)所示,di为使模糊曲线Ci,λ覆盖范围最大的λ,Ci,λ(λ)max和Ci,λ(λ)min为模糊曲线上点值域的最大值和最小值.

|
(4) |
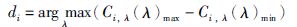
|
(5) |
若得到的Ci,λ(λ)范围越接近y的范围,那么输入变量xi(t-λ)的重要程度越高,对Ci,λ(λ)覆盖范围进行排序,可以得到各自的重要性.基于该原理,本文利用FCA方法提取过程各变量的最优时滞参数di进行软测量建模数据重构.
3.2 TDGPR在线建模为了防止软测量模型随过程动态变化性能不断下降,需要自适应且不频繁更新在线模型来跟踪对象的逐渐变化.TD模型不存在模型重建的问题,具有较高的稳定性,能够同时适应输入输出变量的漂移[17].因此,本文基于TD思想建立在线软测量模型.
训练TD模型时,首先对输入和输出变量计算时间差分ΔXj(t)、 Δyj(t)(j为差分阶次):
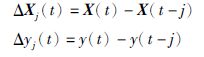
|
(6) |
对于ΔXj(t)与Δyj(t),可以采用数据驱动的方法对其之间关系进行回归,满足Δyj(t)=f(ΔXj(t))+e(t).由于GPR[20-21]方法能够很好地描述过程非线性特性,本文采用该方法建立时间差分数据间的回归模型.当t+1时刻的新数据到来时,采用TDGPR方法得到的预测值yj,pred(t+1),计算方式如下:

|
(7) |
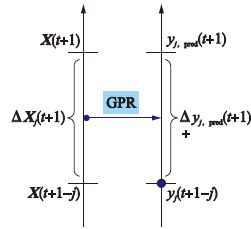
在实际工业过程中,会出现仪表损坏或实验室分析滞后的情况,主导变量的获得时间间隔很大且数量很少,以及数据库中已有主导变量分析值缺失等情况.这样一来,由图 1所示,对于新到来的测试数据X(t+1),以j时刻前数据库保存的yj(t+1-j)为基准,可以得到t+1时刻的主导变量预测值.
|
| 图 1 TDGPR方法建模示意图 Figure 1 TDGPR method modeling diagram |
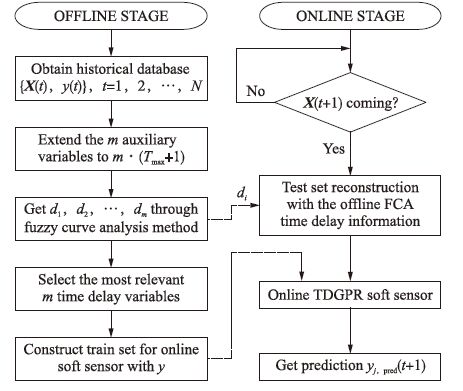
本文提出的采用模糊曲线分析方法确定过程变量时延信息,并在线建立起时间差高斯过程回归的软测量建模流程如图 2所示.
|
| 图 2 FCA-TDGPR方法建模流程图 Figure 2 FCA-TDGPR method modelling flow chart |
本文具体的建模步骤说明如下:
Step 1 获取原始历史数据{X(t),y(t)},t=1,2,…,N,对数据进行预处理,根据过程机理及经验确定Tmax.
Step 2 对于每个原始变量xi,i∈{1,2,…,m},按式(2)方式分别扩展为Tmax+1维的含时滞的输入变量集xi(t-λ),λ=0,1,…,Tmax.
Step 3 根据3.1节的FCA方法确定含时滞输入变量集中每一个变量的重要性程度,根据式(5)确定最优的时滞变量xi(t-di).
Step 4 利用上一步分析得到的时滞参数d1,d2,…,dm重组用于在线建模的软测量训练样本集.若有新的输入样本X(t+1)到来,则基于历史数据库用同样参数进行重组,并转到Step 5; 否则,等待新数据到来.
Step 5 对重组的训练集、 新数据按照3.2节的方法进行j次时间差分处理(j的大小可根据过程的主导变量获得周期和性质确定),然后建立ΔXj(t+1),Δyj,pred(t+1)间的高斯过程模型,基于历史数据库中已存在的yj(t+1-j),在线模型得到的预测输出yj,pred(t+1)由式(7)计算.
本文选择均方根误差(σRMSE)来评价模型的综合预测能力,y(t+1)为t+1时刻主导变量真值.
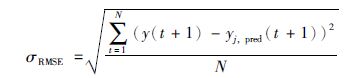
|
(8) |
脱丁烷塔过程是石油炼制生产过程中脱硫和石脑油分离装置的重要组成部分,过程示意图如图 3所示.该过程有7个辅助变量,分别描述为: x1塔顶温度; x2塔顶压力; x3塔顶回流量; x4塔顶产品流出量; x5第6层塔板温度; x6塔底温度1; x7塔底温度2,1个主导变量为塔底丁烷浓度,其值不能直接检测,需要通过在线仪表分析获得.过程数据来自于对真实过程的实时采样,以6 min作为采样间隔共采集了2 394组样本.在线仪表的测量周期和安装位置使得各辅助变量与主导变量间存在大约45 min~90 min的滞后[4],则di的范围约为8~15.仿照文[9]中的做法,本文仿真中将2个塔底温度变量取平均后作为1个辅助变量,同时设置Tmax为19,由此可以得到120个待分析的扩展时滞变量.

|
| 图 3 脱丁烷塔过程原理示意图 Figure 3 Schematic diagram of the Debutanizer column process |
为了验证FCA方法确定时滞参数的可行性,基于历史数据库中已存储的样本对,对6个原始辅助变量扩展后的变量集根据各自对应的模糊曲线覆盖范围确定相应的重要性程度.在不同的训练样本数目n的条件下,通过FCA方法确定的最优时滞变量,如表 1所示.可以看出,随着历史数据库中采集样本数增加,包含的信息越全面,时滞信息越稳定.因此,本文采用n=1 500时确定的时滞参数[14, 16, 10, 17, 14, 19]用于建模数据重构.
| 训练样本数 | FCA方法确定的最优时滞变量 |
| n=900 | x1(t-14),x2(t-16),x3(t-11),x4(t-17),
x5(t-15),x6(t-18) |
| n=1 000 | x1(t-14),x2(t-16),x3(t-11),x4(t-17),
x5(t-13),x6(t-13) |
| n=1 100 | x1(t-14),x2(t-16),x3(t-10),x4(t-16),
x5(t-14),x6(t-14) |
| n=1 200 | x1(t-13),x2(t-16),x3(t-10),x4(t-16),
x5(t-13),x6(t-14) |
| n=1 300 | x1(t-14),x2(t-16),x3(t-10),x4(t-16),
x5(t-14),x6(t-19) |
| n=1 400 | x1(t-14),x2(t-16),x3(t-10),x4(t-16),
x5(t-15),x6(t-19) |
| n=1 500 | x1(t-14),x2(t-16),x3(t-10),x4(t-17),
x5(t-14),x6(t-19) |
如图 4所示,相比于原变量模糊曲线的覆盖范围range 1,引入时滞信息的各变量模糊曲线覆盖范围range 2显著增大,即6个重构变量相比原变量对于主导变量的贡献更大,这样一来为在线建模引入了更加相关的建模数据.同时,为了验证所提方法用于在线估计的有效性,选取2 394组数据中的前1 519组重构1 500组训练样本,后续875组用于在线测试样本,通过4种不同的TD模型对丁烷浓度进行了软测量在线预测.各方法的预测性能指标为σRMSE,仿真对比结果如表 2所示.其中,方法1为不考虑时滞的TDLSSVM方法,方法2为含时滞分析的TDLSSVM方法,方法3为不考虑时滞的TDGPR模型(记为t-TDGPR),本文方法为含时滞分析的TDGPR方法(记为FCA-TDGPR).

|
| 图 4 原变量与最优时滞变量的模糊曲线分布 Figure 4 Fuzzy curve distribution of original variable and optimal time delay variable |
| 模型性能 | 方法1 | 方法2 | 方法3 | 本文方法 |
| j=1 | 0.024 1 | 0.020 2 | 0.015 4 | 0.013 7 |
| j=2 | 0.058 4 | 0.053 6 | 0.030 7 | 0.027 0 |
| j=3 | 0.083 8 | 0.077 8 | 0.045 7 | 0.040 8 |
| j=4 | 0.122 6 | 0.090 8 | 0.061 1 | 0.055 2 |
| j=5 | 0.143 9 | 0.115 6 | 0.076 7 | 0.066 8 |
| j=6 | 0.157 8 | 0.129 9 | 0.091 9 | 0.080 1 |
| j=7 | 0.184 0 | 0.139 0 | 0.106 2 | 0.089 2 |
| j=8 | 0.204 3 | 0.160 3 | 0.120 4 | 0.100 5 |
| j=9 | 0.223 4 | 0.167 4 | 0.133 3 | 0.113 7 |
| j=10 | 0.219 1 | 0.177 7 | 0.145 2 | 0.124 0 |
由表 2可以看出,无论是基于LSSVM[22-23]还是GPR的TD模型,考虑了变量时滞估计的软测量模型性能有了明显的改善,精度显著地优于不考虑时滞的传统建模方法.同时,随着时间差的增加,预测精度不断下降,这是因为基于越近的分析值做出的预测能够越好地追踪当前时刻的过程动态.在各个方法的比较中,本文方法持续保持着最高精度.图 5为FCA-TDGPR与t-TDGPR方法对于丁烷浓度预测结果的散点图,当j从1到10逐渐增加时,基于历史数据库进行预测的时间间隔逐步增大,即使两种方法精度都在下降,但是所提方法的预测结果相比于不考虑时滞的TDGPR方法,在时间差递增时也能较好地贴近丁烷浓度真值,说明了提取的时滞信息符合过程的实际因果关系.仿真图表结果表明: 通过模糊曲线分析方法确定最优时滞参数后,重构的数据对主导变量贡献增强,因此在线模型的精度也显著增强,同时也体现了GPR方法能够很好地解释过程的动态变化,基于TDGPR方法的在线软测量模型能够自适应地基于j时刻前的历史变量值估计当前时刻的丁烷浓度.

|
| 图 5 不同j值情况下的丁烷浓度预测 Figure 5 C4 concentration prediction with different j value |
对于时延过程,考虑到数据库中各个辅助变量对于主导变量存在不同程度的时滞,同时为了不频繁更新模型的跟踪过程动态,本文提出采用模糊曲线分析的方法确定过程最优变量时滞,将时滞信息引入到软测量建模数据中; 然后,利用重构数据集建立TDGPR模型进行在线预测.对脱丁烷塔过程丁烷浓度的仿真实验结果表明: 所提方法能够在历史数据库中样本足够多的情况下,稳定地提取出过程所包含的变量时滞信息且直观有效地挑选出对于主导变量的贡献程度最大的时滞输入变量集; 同时,TDGPR建模方法有效地跟踪了过程输入输出的漂移,模型具有较高的稳定性.相比于传统的稳态零时滞建模方法,显著地改善了预测的精度.即使基于很长时间之前获得的主导变量值,也能够较为准确地预测当前时刻的变量值.对于实际工业过程应用,本文方法为同类型的在线建模问题提供了一种有效的思路.
| [1] | 孙茂伟, 杨慧中. 局部加权混合核偏最小二乘算法及其在软测量中的应用[J]. 信息与控制, 2015, 44 (4): 481–486. Sun M W, Yang H Z. Local weighted mixed kernel partial least squares algorithm and its application in soft-sensing[J]. Information and Control, 2015, 44 (4): 481–486. |
| [2] | 丛秋梅, 苑明哲, 王宏, 等. 基于元学习的污水本质集成软测量模型[J]. 信息与控制, 2015, 43 (2): 248–252. Cong Q M, Yuan M Z, Wang H, et al. Soft-sensor of water quality based on integrated ELM with meta-learning[J]. Information and Control, 2015, 43 (2): 248–252. |
| [3] | Petr K, Bogdan G, Sibylle S. Data-driven soft sensors in the process industry[J]. Computers and Chemical Engineering, 2009, 33 : 795–814. DOI:10.1016/j.compchemeng.2008.12.012 |
| [4] | Fortuna L, Graziani S, Rizzo A, et al. Soft sensors for monitoring and control of industrial processes[M]. Berlin, Germany: Springer-Verlag , 2007 . |
| [5] | Li X L, Su H Y, Chu J. Multiple model soft sensor based on affinity propagation, Gaussian process and bayesian committee machine[J]. Chinese Journal of Chemical Engineering, 2009, 17 (1): 95–99. DOI:10.1016/S1004-9541(09)60039-2 |
| [6] | Fortuna L, Graziani S, Xibilia M G. Soft sensors for product quality monitoring in debutanizer distillation columns[J]. Control Engineering Practice, 2005, 13 (4): 499–508. DOI:10.1016/j.conengprac.2004.04.013 |
| [7] | Komulainen T, Sourander M, Jämsä-Jounela S L. An online application of dynamic PLS to a dearomatization process[J]. Computers and Chemical Engineering, 2004, 28 (12): 2611–2619. DOI:10.1016/j.compchemeng.2004.07.014 |
| [8] | Zhang J, Jin Q B, Xu Y M. Inferential estimation of polymer melt index using sequentially trained bootstrap aggregated neural networks[J]. Chemical Engineering and Technology, 2006, 29 (4): 442–448. DOI:10.1002/(ISSN)1521-4125 |
| [9] | 阮宏镁, 田学民, 王平. 基于联合互信息的动态软测量方法[J]. 化工学报, 2014, 65 (11): 4497–4502. Ruan H M, Tian X M, Wang P. Dynamic soft sensor method based on joint mutual information[J]. CIESC Journal, 2014, 65 (11): 4497–4502. |
| [10] | Lin Y H, Cunningham Ⅲ G A. A new approach to fuzzy-neural system modeling[J]. IEEE Transactions on Fuzzy Systems, 1995, 3 (2): 190–198. DOI:10.1109/91.388173 |
| [11] | Fu Y F, Xu O G, Chen W J.A gross error detecting method based on fuzzy curve weighted MMMD clustering for soft sensor modelling data[C]//11th World Congress on Intelligent Control and Automation.Piscataway, NJ, USA:IEEE, 2014:755-759. |
| [12] | Kadlec P, Gabrys B. Local learning-based adaptive soft sensor for catalyst activation prediction[J]. AIChE Journal, 2010, 57 : 1288–1301. |
| [13] | Xu O G, Liu J F, Fu Y F, et al. Dual updating strategy for moving-window partial least-squares based on model performance assessment[J]. Industrial & Engineering Chemistry research, 2015, 54 : 5273–5284. |
| [14] | Matias T, Souza F, Araujo R, et al. On-line sequential extreme learning machine based on recursive partial least squares[J]. Journal of Process Control, 2015, 27 : 15–21. DOI:10.1016/j.jprocont.2015.01.004 |
| [15] | Liu Y Q, Huang D P, Li Y. Development of interval soft sensors using enhanced just-in-time learning and inductive confidence predictor[J]. Industrial & Engineering Chemistry research, 2012, 51 (8): 3356–3367. |
| [16] | Fujiwara K, Kano M, Hasebe S, et al. Soft-sensor development using correlation-based just-in-time modeling[J]. AIChE Journal, 2009, 55 (7): 1754–1765. DOI:10.1002/aic.v55:7 |
| [17] | Hiromasa K, Takeshi O, Kimito F. Selective use of adaptive soft sensors based on process state[J]. Industrial & Engineering Chemistry research, 2014, 53 : 15962–15968. |
| [18] | Hiromasa K, Kimito F. Moving window and just-in-time soft sensor model based on time differences considering a small number of measurements[J]. Industrial & Engineering Chemistry research, 2015, 54 : 700–704. |
| [19] | Hiromasa K, Kimito F. Maintanenance-free soft sensor models with time difference of process variables[J]. Chemometrics and Intelligent Laboratory Systems, 2011, 107 : 312–317. DOI:10.1016/j.chemolab.2011.04.016 |
| [20] | Rasmussen C E, Williams C K I. Gaussian processes for machine learning[M]. Cambridge, USA: The MIT Press , 2006 . |
| [21] | Bishop C M. Pattern recognition and machine learning[M]. Berlin, Germany: Springer , 2006 . |
| [22] | 李卫, 杨煜普, 王娜. 基于核模糊聚类的多模型LSSVM回归建模[J]. 控制与决策, 2008, 23 (5): 560–564. Li W, Yang Y P, Wang N. Multi-model LSSVM regression modeling based on kernel fuzzy clustering[J]. Control and Decision, 2008, 23 (5): 560–564. |
| [23] | 熊伟丽, 姚乐, 徐保国. 混沌最小二乘支持向量机及其在发酵过程建模中的应用[J]. 化工学报, 2013, 64 (12): 4585–4591. Xiong W L, Yao L, Xu B G. Chaos least squares support vector machine and its application on fermentation process modeling[J]. CIESC Journal, 2013, 64 (12): 4585–4591. |



