1 引言
群机器人是特殊的多机器人系统,由许多个无差别的自治机器人组成,具有典型的分布式系统特征.主要研究能力有限的个体机器人通过交互,协调和控制涌现群体智能以合作完成相对复杂的规定任务[1-4].其中协作搬运是群机器人学中的一个重要研究方向,由于具有广泛的应用前景所以受到了众多研究者的关注和重视[5-9].基于抓握(grasping based)和基于囚笼(caging based)的方法是协作搬运问题的两类最基本最常用的解决方法.
基于抓握的方法常要通过机器人与物体的接触以形成力锁合和形态锁合(force closure and form closure).因为这两个条件意味着系统可以抵御作用在物体上的任何外力、 可以让物体产生需要的加速度[6, 10-12].力锁合通常仅由机器人的接触力产生.若其中还包含一些作用在机器人上的外力,如重力与摩擦力等,则称为条件力锁合.文[13-14]等运用条件力锁合来完成多机器人的协作推箱等任务.
基于囚笼的方法则常要求系统能够满足物体锁合(object closure)条件[6, 12, 15-18].在该条件下,物体能在一个较小的囚笼内运动,机器人与物体之间也不需要时刻地保持接触.因此与力锁合相比,物体锁合使得机器人的运动规划和控制更加简单,鲁棒性更强,机器人间的协调协作也更加容易实现.
文[12, 17-18]等基于物体锁合条件给出了协作搬运问题的一个解决方法,其基本步骤为: 第1步,基于人工势场方法各机器人首先都独立地从自己的初始位置运动到搬运物体的附近.第2步,在各机器人控制器的控制下,机器人环绕着物体形成一个可以囚住物体的搬运队形.第3步,队形控制策略控制着搬运队形协调运动从而完成搬运任务.
上述方法的第1步与第2步采用完全分散的方式以形成满足物体锁合条件的搬运队形有许多优势.如计算负担低、 机器人间通信量少、 机器人数量的可扩展性强等.但这种方法仅适合机器人数量少且搬运物体形状较简单的情况.当机器人的数量很多且搬运物体的形状复杂时,上述方法不但难以保证形成满足条件的搬运队形,且即使能形成所用的时间也会很长,即效率很低.
基于上述原因,本文受到人们在求职或变更自己职位时常要遵守的规则的启发,提出了一种自组织确定各机器人搬运点并最终形成搬运队形的人工社会职位法.该方法中首先给出了人工社会职位法的基本规则,并运用人工社会职位法的基本规则确定各机器人每个采样时刻的对应搬运点.然后每一个采样时刻改进的人工力矩控制器驱动机器人向各自的搬运点运动一步.最终每个机器人都能安全准确的到达一个不同于其它机器人的搬运点,从而形成搬运队形.该方法不仅原理简单、 计算量少,而且无论机器人的数量是多少,搬运物体的形状多复杂,系统总能在有限的时间内形成满足条件的搬运队形.本文还改进了文[19-20]中给出的求解吸引线段与吸引点的算法从而显著地降低了计算量.仿真结果表明,文中所给方法是可行且有效的.
2 系统模型和问题描述本文的研究基础是如果有m个机器人参与搬运,则系统已经根据搬运物体形状确定了满足如下条件的m个搬运点: 当每个搬运点上都有一个具有给定位姿的机器人时,系统就能满足力锁合或物体锁合条件.如在图 1中,系统有8个机器人,所以围绕搬运物体有且只有8个搬运点.
搬运点模型是一个有基本运动方向线(PMDline)的质点,如图 1中的T1~T8所示.搬运点的PMDline指示着它的位姿或者搬运队形下一步的行进方向.

|
| 图 1 系统模型 Figure 1 System model |
个体机器人Ri(i=1,2,…,m)的模型与文[20]中相同,是一个半径为DR、 有一条PMDline的圆.然而搬运点的PMDline是一条射线,Ri的PMDline却是一条从Ri中心PRi出发、 长度为SMR的有向线段,其中SMR是机器人的最大运动步幅.机器人的PMDline具有很多用途,详见文[20].
系统中每个机器人的地位都是平等的,没有主次之分.Ri除了知道所有搬运点位置外,对其它环境都没有任何先验知识,必须使用它的传感器去感知它周边的环境和其它机器人.Ri的传感器是全方位的,其有效半径为DV.对于环境中的任意一点F,只有当PRiF不通过任何障碍和其它机器人且PRiF≤DV时,F才能被Ri探测到.为了尽可能地减少机器人间的通信量以提高算法的实时性,如果Ri探测到另一个机器人Rj,Ri才知道且仅知道Rj的位置、PMDline方向和对应搬运点.
假设1 若Ti在机器人Ri的探测范围内且在Ri的探测范围之内的所有机器人的搬运点都不为Ti,则机器人Ri认为搬运点Ti是空缺的.
后文的其它概念如不声明则都与文[19]中的完全相同.限于篇幅,本文不再详述,详见文[19].
初始时刻,假定所有机器人都在搬运物体附近.所以在本文中,除了搬运物体外不再考虑其它障碍.
注1 一条有向线(射线、有向线段)绕着它的端点旋转到与全局坐标系X轴方向相同时所转的绝对值不大于π的有向角称为该有向线的方向角[16-17].设βi为有向线li的方向角,βj为有向线lj的方向角,函数g(x)如式(1)所示,则β=g(βi-βj)就是从li到lj的角.

|
(1) |
其中
注2 文中,PRi表示机器人Ri的位置(中心); 符号L(A,B)表示从A点出发经过B点的射线; A1A2表示端点为A1和A2的线段; A1A2为线段A1A2的长度; β(A,B)为有向线段AB的方向角; DS为与机器人安全相关的一个重要常数; λa为一个大于0.5且小于1的正常数.
3 人工社会职位法确定机器人搬运点因为在自组织控制系统中不存在能对其它机器人发一些命令或指令的主机器人,个体机器人的地位相同且只能利用通过探测或通信得到一些局部信息,所以自组织形成群机器人复杂搬运队形的关键在于各机器人如何仅根据局部可用的信息,自主地确定自己的搬运点.
本文受到人们在求职或变更职位时常遵守的如下规则的启发而提出一种自组织确定各机器人搬运点的人工社会职位法.
规则1 初次求职时,人们总是申请与自己能力最接近的职位.
规则2 一个已有职位的人如果发现上一级职位空缺,则会主动放弃现职位去竞争上一级职位.也就是说,只要发现它的上一级职位空缺它就会想升迁.
注3 这一规则可以尽可能地保证上级职位不出现空缺.
规则3 一个已有职位的人如果它的职位被另一个更有能力的人抢占,则它通常可以直接获得比这个职位低一级的职位而不用考虑低一级职位是否有人担任.但通常情况下该人不会急着到新职位去履职而会等待一段时间,其中时间的长短与新旧职位间的差别有关,因为从概率论的观点看,职位被抢占是个概率事件,他还有继续获得该职位的可能.
注4 这一规则可以保证职位能够有序地变更.
上述3个规则是人工社会职位法的理论基础,也是该方法名称的由来.
如果按逆时针(规定方向是为了讨论的方便)的绕行方向对所有搬运点依次编号,并规定序号小搬运点的等级高于序号大的搬运点,序号最大的搬运点又是序号为0的搬运点,即又是序号最小的最高级的搬运点,则所有搬运点就构成了一个特殊的循环式的人工社会职位体系.
图 1中T8又是T0.所以下面叙述中,如果Tpi-1的下标pi-1=0则为搬运点Tm,Tpi+1的下标pi+1=m+1则为搬运点T1.
然后把每个机器人看作一个求职者,每个搬运点看作一个职位,则各机器人搬运点的确定问题就可用求职者确定自己职位的方法解决.
上述就是人工社会职位法的基本思想与原理.基于人工社会职位法确定机器人Ri在当前时刻tk搬运点的具体方法如算法1所示.
算法1 tk时刻机器人Ri搬运点的确定:
Step 1 若tk=t0,则根据规则1,Ri将距离自己最近的搬运点选为自己当前时刻的搬运点.否则转Step 2.
Step 2 若Ri发现其tk-1时刻搬运点的上级Tpi-1空缺,对任意能被Ri探测且其上个时刻搬运点也是Tpi的机器人Rq,Ri到Tpi-1的距离都比Rq到Tpi-1的距离近,则根据规则2,Ri将Tpi-1选为自己当前时刻的搬运点; 否则,转Step 3.
Step 3 若有能被Ri探测到的机器人Rq1,Rq2,…,Rqt,它们在tk-1时刻的搬运点也是Tpi,RiTpi+1<max(Rq1Tpi+1,Rq2Tpi+1,…,RqtTpi+1)且Ri可探测到Tpi及RiTpi<TpiTpi+1+DS,则根据规则3,将tk时刻Ri的搬运点变更为Tpi+1; 否则,转Step 4.
Step 4 若Ri探测不到它tk-1时刻的搬运点Tpi或者它的吸引线段不为空,但Ri能探测到另一个空缺搬运点Tq且低于tk-1时刻搬运点Tpi不超过m/2个等级,则将tk时刻Ri的搬运点变更为Tq; 否则,Ri的搬运点仍为Tpi.
关于算法1的计算复杂度,显然可以用它在最坏情况下需要的比较次数来计算.设在Ri探测到的机器人中,上个时刻与Ri有相同搬运点的机器人有t个,则Step 2在最坏情况下需要t次比较;Step 3在最坏情况需要t+1次比较;Step 4需要1次比较.因此算法1在最坏情况下需要2t+2(≤2m)次比较,即算法1的时间复杂度为O(2m).所以算法1的时间复杂度非常低.
4 吸引点的改进计算与人工力矩运动控制器确定了各机器人tk时刻的搬运点后,各机器人在各自运动控制器的控制下向着tk时刻自己的搬运点运动.采用文[20]设计的人工力矩运动控制器是一个比较好的选择.这是因为该运动控制器具有许多优点,如能让机器人穿过狭窄的通道和到达距离障碍很近的目标且到达后还能具有给定的位姿,在复杂拥挤的环境下能快速地化解机器人间的冲突和保证机器人的安全等.
人工力矩运动控制器的基本思想是: 在当前时刻tk,机器人Ri可能受到3种人工力矩的影响,即它的吸引点Pati对它的吸引矩,危墙代表点对它的排斥矩及协调同伴对它的协调矩.在合力矩的作用下,Ri沿着合力矩的梯度方向改变它的位置和PMDline方向以使这些力矩能够快速地增加.另外,Ri沿着它的PMDline还有一个几乎不受人工力矩影响的运动分量(Sxi(k+1),Syi(k+1))T,它和人工力矩函数一起决定着Ri下个时刻的位置和PMDline方向.下个采样时刻,重复上述步骤直到系统任务结束.
从人工力矩运动控制器的基本思想可以看出: Ri在tk时刻需先计算出它的吸引点Pati以引导自己绕过障碍物沿着较优的路径运动.而本文中机器人向着各自搬运点运动中会出现被搬运物体阻断的情况,因此在该情况下需要求解吸引线段来引导机器人绕过搬运物安全的达到搬运点.文[17]给出了一种求解吸引线段的方法,但该方法的计算量大且难以理解.本文根据机器人当前时刻探测到的局部信息提出了一种计算吸引线段的新方法.
设各机器人把tk时刻探测到的搬运物体边缘线以有向线段的形式保存在W{i}中.W的结构是W=[A1B1,A2B2,…,AnBn].其中有向线段AnBn的方向与本文的参考方向一致.
结论1 如果机器人Ri探测到自己与搬运点Tpi之间被搬运物体阻断,那么在W{i}中必然存在一条阻断PRiTpi的线段AB.
计算Ri的吸引线段方法如下:
令Asti、 Aendi分别表示Ri吸引线段的起点与终点.计算Ri的吸引线段就是分别计算出Asti和Aendi.通常情况下需先求出Asti.当PRiTpi被搬运物体阻断时,很容易得到一条阻断PRiTpi的线段AB.显然Asti可能是A或B.
Asti的求解分3种情况:
(1) tk时刻的Tpi不同于tk-1时刻Tpi(k-1).该情况下只有tk时刻的Tpi是tk-1时刻的下级搬运点才会出现PRiTpi被阻断的情况,所以Ri向着搬运点的降级方向运动,即逆时针方向.所以此时Ri的Asti应该为B.
(2) tk时刻的Tpi与tk-1时刻Tpi(k-1)时相同且Asti(k-1)为空.这种情况下说明上个时刻PRi(k-1)Tpi没有被搬运物阻断.Ri应该由PRi向PRi(k-1)方向运动,则选择A和B中与PRi(k-1)在直线L(PRi,Tpi)同一边的点为Asti.
(3) tk时刻的Tpi与tk-1时刻Tpi(k-1)时相同且Asti(k-1)不为空.该情况下Ri的运动方向不需要改变,则选择A和B中与PRi(k-1)在直线L(PRi,Tpi)两边的点为Asti.
得到Asti后,按照如下方法计算Aendi: 若Asti=B,Ri是沿着搬运物体边缘A到B的方向运动,即逆时针的方向,则令s=-1; 若Asti=A,Ri是沿着搬运物体边缘B到A的方向运动,即顺时针的方向,则令s=1.Aendi是满足g(β(Asti,Aendi)-β(PRi,Asti))=s×π/2且AstiAendi=λaDS的一个点.
根据上述方法即可求得Ri的吸引线段.
算法2 tk时刻吸引线段与吸引点的计算:
Step 1 若PRiTpi被搬运物阻断,则执行Step 1.1~Step 1.3.
Step 1.1 如果Asti不为空且PRi到L(Asti(k-1),Aendi(k-1))的距离大于SMR,令Asti=Asti(k-1),Aendi=Aendi(k-1),转Step 3.
Step 1.2 如果Tpi不同于Tpi(k-1),则Asti=B,s=-1并计算Aendi,转Step 3; 否则,转Step 1.3.
Step 1.3 若Asti为空,则令f=sgn(g(β(PRi,PRi(k-1))-β(PRi,Tpi))); 若Asti不为空,则令f=-sgn(g(β(PRi,PRi(k-1))-β(PRi,Tpi))).如果sgn(g(β(PRi,A)-β(PRi,Tpi)))=f,则Asti=A,s=1; 否则,Asti=B,s=-1.计算Aendi,转Step 3.
Step 2 若PRiTpi没有被搬运物阻断,则执行Step 2.1.
Step 2.1 如果Asti不为空且PRi到L(Asti(k-1),Aendi(k-1))的距离大于SMR,则令Asti=Asti(k-1),Aendi=Aendi(k-1),转Step 3; 否则,令Pati=Tpi,清空Asti和Aendi并结束算法.
Step 3 令Pati=Aendi,结束算法.
算法2 求解新的吸引线段时,Asti很容易得到,只需要判断Asti是阻断线段AB上的A点还是B点即可,然后根据Asti计算Aendi即可求出Ri的吸引线段.因此其计算量明显小于文[20]给出的方法.
人工社会职位法自组织形成复杂搬运队形的一般步骤如算法3所示.
算法3 复杂搬运队形自组织形成的步骤:
Step 1 初始化所有机器人的位置; 输入搬运物体形状、 所有搬运点,规定参考方向; 输入系统参数; 令tk=t0.
Step 2 根据人工社会职位法的规则1得到初始时刻Ri(i=1,2,…,m)的搬运点.
Step 3 For Ri(i=1,2,…,m),执行如下步骤:
Step 3.1 如果Ri已到达了它的搬运点且没有协调同伴,则Ri保持静止.否则,执行Step 3.2~Step 3.4.
Step 3.2 如果k>0,则运用算法1得到Ri的搬运点.
Step 3.3 运用算法2计算出Pati、 Asti和Aendi.
Step 3.4 运用文[20]中的人工力矩运动控制器控制Ri运动一步到达下个时刻与位置.
Step 4 End for
Step 5 如果每个机器人都到达了它的搬运点,则结束算法; 否则,令tk=tk+1,然后转Step 3.
据算法3可得: 与文[12, 17-18]中的方法相比,本文中的方法更适用于一般的情况,因为文[12, 17-18]给出的方法只适合简单的凸多边形搬运物体,无法形成本文仿真中的复杂搬运队形.与文[21]中的方法相比,本文给出的方法不会出现文[21]中主机器人出现故障将导致整个系统瘫痪、 一旦搬运物体的形状发生变化就需要重新规划等问题.主要原因是由于本文中提出的是一种自组织的形成方法,系统中不存在一个主机器人,所以即使个别机器人出现故障也不会影响到其它机器人的运动.
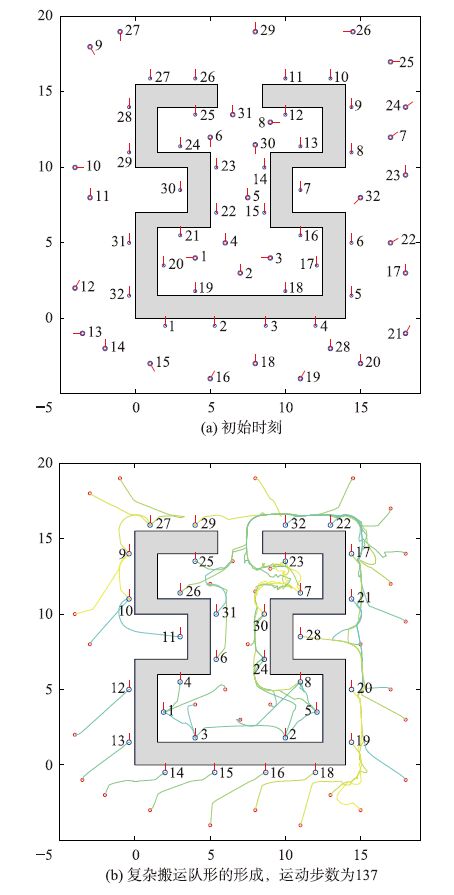
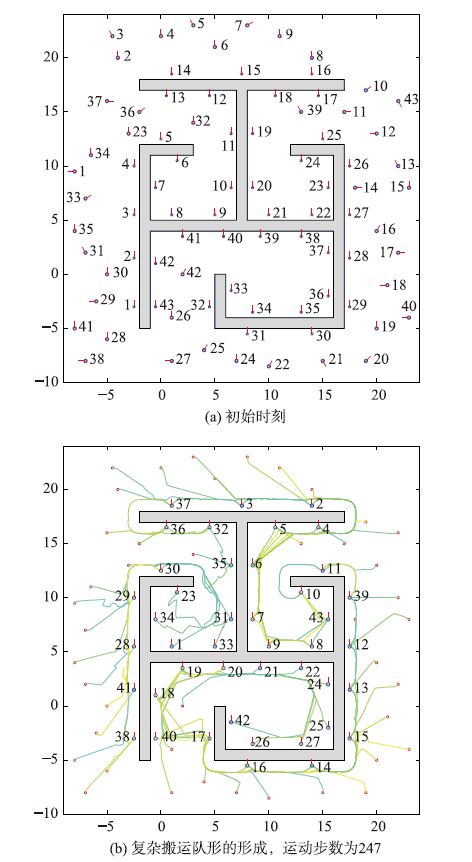
5 仿真结果与分析为了检验文中有关理论和方法的可行及有效性,本文做了大量的仿真,图 2~图 4给出了几个具有代表性的仿真,分别为25、 32、 43个机器人在不同环境中自组织形成复杂搬运队形的仿真.

|
| 图 2 25个机器人形成复杂搬运队形的仿真 Figure 2 Simulation for 25 robots to form a complex transport formation |
|
| 图 3 32个机器人形成复杂搬运队形的仿真 Figure 3 Simulation for 32 robots to form a complex transport formation |
|
| 图 4 43个机器人形成复杂搬运队形的仿真 Figure 4 Simulation for 43 robots to form a complex transport formation |
在该仿真中,系统部分参数值如表 1所示.图 2(a)、3(a)、 4(a)中,小的带有基本运动方向线的圆圈表示搬运点; 大的带有基本方向线的圆圈表示机器人; 机器人与搬运点旁边的一组数字是其对应的序号; 图 2(b)、3(b)、4(b)中的彩色实线是机器人在自组织形成复杂搬运队形中留下的实际运动轨迹,小的红色圆圈是机器人的初始位置.
从图 2(b)、3(b)、 4(b)中可以看出,在3个仿真中,各机器人都能有序地变更自己的搬运点,最终都能自组织快速地运动到一个不同于其它机器人的搬运点并形成给定的搬运队形.从而证明了本文所给出的自组织确定各机器人搬运点的方法是可行且有效的.
另外,从图 2(b)、3(b)、4(b)中还可以看出,当各机器人到自己的搬运点被搬运物体阻断时,各机器人都能够光滑地绕过搬运物安全地到达搬运点,同时到达后还能具有与搬运点相同的位姿,从而证明了文中给出的关于吸引线段及吸引点的计算方法是可行且有效的.
在系统已经根据搬运物体形状和机器人数量确定了所有搬运点的前提下,本文针对群机器人搬运队形的形成问题提出了一种自组织的人工社会职位法.该方法原理简单计算量小且无论机器人的数量是多少,无论搬运物体的形状多复杂,系统总能快速地形成满足条件的搬运队形.
另外本文还改进了现有人工力矩运动控制器中吸引线段与吸引点的计算方法.改进方法不但原理易懂求解简单且降低了计算量.
下一阶段,本文将研究如何继续改进现有的人工力矩运动控制器,使其能够驱动群机器人队形协调地运动以把物体从初始位置拖拉或搬运到给定的目标位置.
| [1] | 薛松东, 曾建潮. 群机器人的研究综述[J]. 模式识别与人工智能, 2008, 21 (2): 177–185. Xue S D, Zeng J C. Swarm robotic:A survey[J]. Pattern Recognition and Artificial Intelligence, 2008, 21 (2): 177–185. |
| [2] | 张云正, 薛松东, 曾建潮. 群机器人多目标搜索中的合作协同和竞争协同[J]. 机器人, 2015, 37 (2): 142–151. Zhang Y Z, Xue S D, Zeng J C. Cooperative and competitive coordination in swarm robotic search for multiple targets[J]. Robot, 2015, 37 (2): 142–151. |
| [3] | 张云正, 薛松东, 曾建潮. 群机器人多目标搜索中带闭环调节的动态任务分工[J]. 机器人, 2014, 36 (1): 57–68. |
| [4] | 黄天云, 陈雪波, 徐望宝, 等. 基于松散偏好规则的群体机器人系统自组织协作围捕[J]. 自动化学报, 2013, 39 (1): 57–68. Huang T Y, Chen X B, Xu W B, et al. A self-organizing cooperative hunting by swarm robotic systems based on loose-preference rule[J]. Acta Automatica Sinica, 2013, 39 (1): 57–68. DOI:10.1016/S1874-1029(13)60007-5 |
| [5] | Miyata N, Ota J, Arai T, et al. Cooperative transport by multiple mobile robots in unknown static environments associated with real-time task assignment[J]. IEEE Transactions on Robotics and Automation, 2002, 18 (5): 769–780. DOI:10.1109/TRA.2002.803464 |
| [6] | Wang Z D, Nakano E, Takahashi T. Solving function distribution and behavior design problem for cooperative object handling by multiple mobile robots[J]. IEEE Transactions on Systems, Man, and Cyberneticsn-Part A:Systems and Human, 2003, 33 (5): 537–549. DOI:10.1109/TSMCA.2003.817396 |
| [7] | Pereira G A S, Kumar V, Campos M F M. Decentralized algorithm for multi-robot manipulation via caging[J]. The International Journal of Robotics Research, 2004, 23 (7/8): 783–795. |
| [8] | Sieber D, Deroo F, Hirche S. Formation-based approach for multi-robot cooperative manipulation based on optimal control design[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ, USA:IEEE, 2013, 5227-5233. |
| [9] | Wu M H, Konno A, Ogawa S, et al. Symmetry cooperative object transportation by multiple humanoid robots[C]//Proceedings of IEEE International Conference on Robotics and Automation. Piscataway, NJ, USA:IEEE, 2014:3446-3451. |
| [10] | Nakamura Y, Nagai K, and Yoshikawa T. Dynamics and stability in coordination of multiple robotic mechanisms[J]. The International Journal of Robotics Research, 1989, 8 (2): 44–61. DOI:10.1177/027836498900800204 |
| [11] | Rus D. Coordinated manipulation of objects in a plane[J]. Algorithmica, 1997, 19 (1/2): 129–147. |
| [12] | Wang Z D, Hirata Y, Kosuge K. Control a rigid caging formation for cooperative object transportation by multiple mobile robots[C]//Proceedings of the IEEE International Conference on Robotics and Automation. New Orleans, USA:IEEE, 2004:1580-1585. |
| [13] | Lynch K M, Mason M T. Stable pushing:Mechanics, controllability, and planning[J]. The International Journal of Robotics Research, 1996, 15 (6): 533–556. DOI:10.1177/027836499601500602 |
| [14] | Parker L E. Alliance:An architecture for fault tolerant multi-robot cooperation[J]. IEEE transactions on Robotics and Automation, 1998, 14 (2): 220–240. DOI:10.1109/70.681242 |
| [15] | Rimon E, Blake A. Caging planar bodies by one-parameter two fingered gripping systems[J]. The International Journal of Robotics Research, 1999, 18 (3): 299–318. DOI:10.1177/02783649922066222 |
| [16] | Sudsang A, Rothganger F, Ponce J. Motion planning for disc-shaped robots pushing a polygonal object in the plane[J]. IEEE Transactions on Robotics and Automation, 2002, 18 (4): 550–562. DOI:10.1109/TRA.2002.801049 |
| [17] | Wang Z D, and Kumar V. Object closure and manipulation by multiple cooperating mobile robots[C]//Proceedings of IEEE International Conference on Robotics and Automation(ICRA). Piscataway, NJ, USA:IEEE, 2002:394-399. |
| [18] | Wang Z D, and Kumar V. A Decentralized test algorithm for object closure by multiple cooperating mobile robots[J]. Distributed Autonomous Robotic Systems, 2002, 5 : 165–174. |
| [19] | Xu W B, Liu X P, Chen X B, et al. Improved artificial moment method for decentralized local path planning of multi-robot[J]. IEEE Transactions on Control Systems Technology, 2015, 23 (6): 2383–2390. DOI:10.1109/TCST.2015.2402231 |
| [20] | Xu W B, Chen X B, Zhao J, et al. Function segment artificial moment method for sensor-based path planning of single robot in complex dynamical environments[J]. Information Sciences, 2014, 280 (1): 64–81. |
| [21] | 黄天云, 王晓楠, 陈雪波. 基于队形控制的多机器人时间最优搬运方法[J]. 系统仿真学报, 2010, 22 (6): 1442–1446. Huang T Y, Wang X N, Chen X B. Multirobot time-optimal handling method based on formation control[J]. Journal of System Simulation, 2010, 22 (6): 1442–1446. |



