2. 中国科学院大学, 北京 100049;
3. 沈阳中科博微科技股份有限公司, 辽宁 沈阳 110179
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Microcyber Corporation, Shenyang 110179, China
1 引言
模型预测控制(model predictive control,MPC)是20世纪70年代产生于工业过程控制领域的一类计算机控制方法,经典算法主要包括动态矩阵控制(dynamic matrix control,DMC)、 模型算法控制(model algorithmic control,MAC)、 广义预测控制(generalized predictive control,GPC)[1-4].模型预测控制能够处理有约束、 多变量工业过程控制问题[5-7],现在已广泛应用于石油、 化工、 食品及航空等领域[8].模型预测控制在诸多领域成功应用的同时,有关MPC系统的故障问题被越来越多的研究者所关注.
控制系统的故障大体可以分为被控对象故障、执行器故障,传感器故障和控制器故障.在现如今的计算机控制系统中,执行器故障和传感器故障是导致控制系统失效的主要原因.据统计,控制系统80%以上的异常由上述两种故障导致[9].针对这两类故障,学者们大多从故障容错控制及数据补偿等方面进行研究.Pranatyasto、 Qin等针对催化裂化装置的模型预测控制系统,采用主成分分析法(principal component analysis,PCA)实现了传感器数据验证、 过程故障识别,通过重构误差对故障数据进行补偿,取得了理想的控制效果[10-11].由于执行器故障直接影响着整个系统的控制策略,所以执行器的可靠性极为关键,常对其进行容错控制,使得当执行器发生故障时,系统仍能保证稳定性[12].文[13]针对执行器卡死故障,提出基于迭代学习观测器的容错控制方法.文[14]采用自适应滑模变结构跟踪控制技术,设计故障补偿的容错控制算法,保证了执行器故障在未知时间发生时系统的稳定性.输出端传感器常见故障有失效,大噪声等.文[15]采用在线辨识的方式,递推得到扰动的时间序列模型,改进了预测控制的抗扰动性能.文[16]通过计算每个输出变量的预测误差的加权平方和来改变对角CARIMA模型的权重,设计出抗扰动广义预测控制算法.
失效和卡死是执行器常见的故障,这两种情形影响到控制系统的结构,这使得容错控制器的设计并不容易实现.而输出传感器的失效故障同样会使控制系统的结构发生改变,模型预测控制变量间的强耦合性也使得输出抗扰动难以设计.本文针对执行器故障、 输出传感器故障影响控制系统结构的特点,在假定故障已被定位的前提下,分析系统输入输出变量稳态关系,提出变结构DMC控制方法.
2 DMC算法简介对于一般的多变量过程,假设该过程包含m个控制输入和p个输出,假定已测得每个输出yi对每一个控制输入的uj的阶跃响应aij(t),则可由它们在采样点上的值组成模型向量:
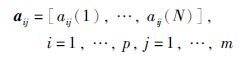
|
(1) |
该模型即为多变量DMC的数学模型.DMC的特征主要包括3部分: 预测模型、 滚动优化及反馈校正[17].
假设m个控制输入从k时刻起均有M次变化,经过推导可得多步预测模型:
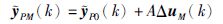
|
(2) |
其中,P、 M分别为预测时域和控制时域,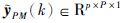
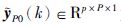
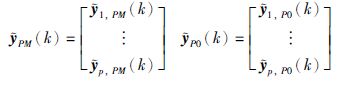
|
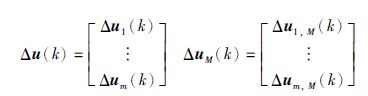
|
在滚动优化过程中,每一个控制周期极小化如下的性能指标:
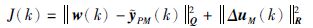
|
(3) |
其中,w(k)为被控输出的设定点,Q为输出变量误差加权矩阵,R为输入增量控制加权矩阵:
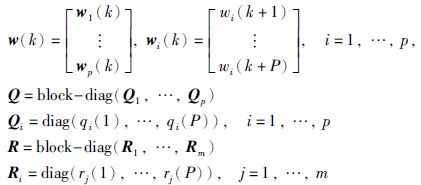
|
在无约束情况下,由多步预测模型(2)可计算出最优控制增量:
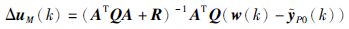
|
(4) |
反馈校正的过程此处不再赘述.
3 输入输出故障模拟DMC控制过程中多个变量之间有极强的耦合性,某一个异常的控制输入将可能导致所有输出的异常变化; 同样,由于DMC的反馈校正环节是基于被控对象的输出采样的,采样过程中的扰动、 噪声等将影响到控制输入的计算,近年来针对抗扰动预测控制问题已经有了广泛的研究[18-19].本文提出的变结构控制,主要针对输入执行器失效、 输出传感器失效或存在极大测量噪声等故障问题,这类故障的发生可能对控制系统产生灾难性影响,而且通常无法以对扰动进行处理的方式解决.以Shell benchmark重油分馏塔模型为例来说明此类故障对系统的影响.采用DMC控制算法,仿真过程为标称系统,即控制器模型和分馏塔模型相同.Shell benchmark重油分馏塔模型为
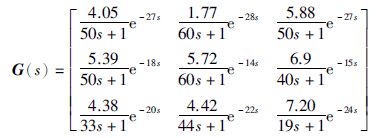
|
(5) |
过程变量包括3个操作变量和3个被控输出变量,输出目标设为y=[0.5,-0.5,0.5]T,Q、 R均取单位阵,预测时域P=120,控制时域M=20.输入端模拟第3路输入执行机构失效的故障,令故障从0时刻开始,即u3(k)=0,k=0,1,2,….各变量已进行归一化处理.图 1中点线为无故障时的仿真曲线,实线为故障时的仿真曲线.从仿真结果可以清晰地看出此类输入故障导致控制器无法实现控制目标,系统在稳定后通常各个输出端都存在很大的静差.
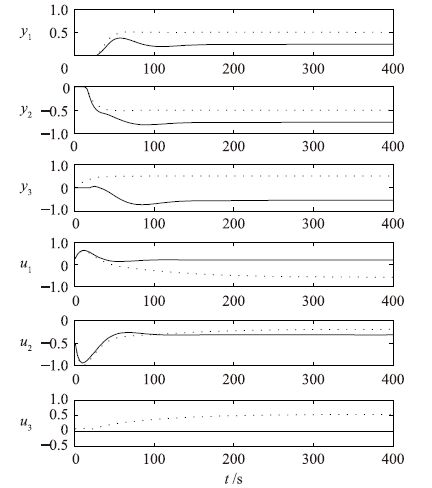
|
| 图 1 第3路输入故障仿真 Figure 1 Simulation of the third input fault |
输出端模拟采样传感器的测量故障,从0时刻起,在第3路输出上增加随机扰动,扰动范围为-0.1~0.1.输出目标设为y=[0.5,-0.5,0.5]T,误差权矩阵Q、 控制权矩阵R均取单位阵,预测时域P=120,控制时域M=20.故障仿真结果如图 2所示.
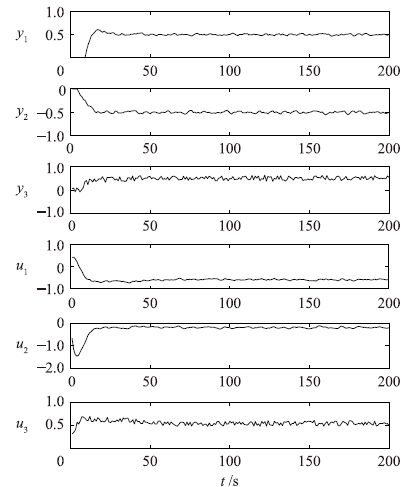
|
| 图 2 第3路输出传感器故障仿真 Figure 2 Simulation of the third output sensor fault |
从仿真结果来看,控制器虽然能够使系统状态向控制目标移动,但由于大量测量噪声的存在影响了控制器对控制增量的计算,使得控制输入频繁地抖动,而输出则在期望的目标值附近震荡.在噪声较大的时候,控制效果会变得很差,并且输入执行器的非正常频繁动作会降低其使用寿命.
4 DMC变结构控制故障诊断的理论研究与工程实践已经发展得相对成熟,关于故障诊断不在本文所讨论的范围内,本文内容假设故障已经被准确定位.本节将对多变量控制系统控制输入的稳态值与被控输出稳态值之间的关系进行说明,然后分别给出针对过程输出端故障和输入端故障情况下的变结构模型预测控制方法.
4.1 多变量过程输入稳态值与输出稳态值的关系根据文[20]中已证明的定理1可知,输入变量稳态值的变化最终决定了输出变量的稳态值.根据系统输入变量和输出变量的个数,可以将多变量系统划分为方系统(输入变量个数等于输出变量个数)、 瘦系统(输入变量个数小于输出变量个数)及胖系统(输入变量个数大于输出变量个数).对于方系统,当过程的稳态增益矩阵可逆时(大多数化工过程都满足),给定一组输出设定点,当系统达到稳态时,必将有唯一的一组稳态输入值与之对应,也就是说两者之间是一一对应的关系.而对于瘦系统和胖系统,其过程稳态增益矩阵不可逆,无法根据稳态增益矩阵和输出设定点直接求得输入稳态值.系统的稳态方程可以被看作以下的非齐次线性方程组:
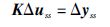
|
(6) |
其中,K为系数矩阵:
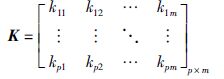
|
系数矩阵K的增广矩阵为

|
根据线性代数的知识,式(6)所表示的m元非齐次线性方程组有解的充分必要条件是rank(K)=rank(B).当rank(K)<rank(B)时,方程组无解.当被控系统为瘦系统时,控制输入m与被控输出p
当输入端执行机构发生故障,使得实际作用于系统的输入增量与控制器计算得到的输入增量不匹配时,将对整个控制系统造成严重的影响,在这种情况下系统输出设定值往往不可达,影响到产品质量、 经济效益甚至生产过程的安全.
当检测到某些输入端发生故障时,改变控制器的结构,将故障的输入从控制器的操作变量中去除.考虑存在m个操作变量、 p个被控输出的多变量过程,其控制器模型使用传递函数矩阵的形式可表示为
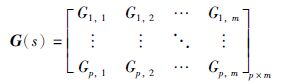
|
其中,Gi,j为第j个输入对第i个被控制输出的传递函数.例如,假定第l(1≤l≤m)个输入通路出现故障,控制器模型变为
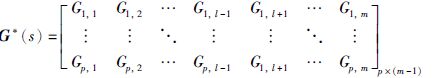
|
此时控制器结构变为m-1个操作变量,p个被控输出.输入端的变结构控制,实际是减少了操作变量自由度,期望控制器在比原来输入自由度低的情况下,尽可能地达到期望的控制目标.
在降低了输入自由度的情况下,控制器新的结构存在3种可能: 胖系统、 方系统及瘦系统.通过4.1小节的分析可知,当不考虑约束条件时,胖系统和方系统总是有解的,即改变控制器结构以后,原来的设定点总是可达.当考虑约束条件时,通过有约束DMC算法求取最优控制增量,也可以适当地放宽约束条件,以达到更好的控制效果.现在着重讨论控制器的结构变为瘦系统的情形.
由4.1小节的分析,瘦系统稳态方程对应的线性方程组中,rank(K)≤rank(B),当且仅当Δyss属于K的列空间时,有rank(K)=rank(B)从而方程组的解存在,即控制目标可达.但实际上通过微小的调整输出设定点也很难满足rank(K)=rank(B).这里提出一种基于输出目标优先级的方法,通过系统稳态增益矩阵的子矩阵,重新计算得到一组新的输出设定点,新的输出设定点保证了优先级高的被控输出达到期望值.当控制器操作变量自由度由m降低为n并且n<p时,将p个被控输出按照安全性、 产品质量以及经济性等因素综合考虑,划分不同的优先级.确定优先级之后,在p个被控输出中按照优先级从高到低的顺序选择n个,按照以下稳态方程求解稳态输入增量:
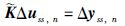
|
(7) |
其中,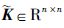
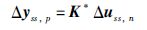
|
(8) |
其中K*∈Rp×n为变结构后的稳态增益矩阵,Δyss,p∈Rp×1为新的输出稳态增量,通过Δyss,p可以得到一组新的输出设定点.改变设定点后,控制器将最大限度地保证优先级较高的n个被控输出达到原先的设定目标,但其余p-n个输出目标将不能得到保证,故在进行输入端变结构控制前,应根据输入目标的优先级和当前输入端故障个数进行变结构控制的可行性判定.
4.3 输出端变结构控制当某些输出端的采样过程发生异常时,不可靠的采样数据将会影响到最优控制增量的计算,从而降低了控制器的性能.在检测到输出端故障的时候,改变控制器的结构,将故障通路的输出从控制器被控输出变量中去除.如,假定第l(1≤l≤m)个输出通路出现故障,控制器模型变为
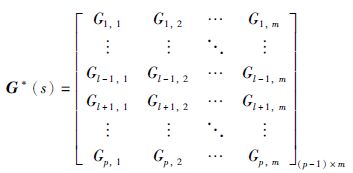
|
控制器不再对存在故障的输出端进行采样,式(3)所表示的性能指标也将其排除在外.假定系统原设定点可达(一般情况下也是必须的),则有一组控制输入稳态值与其对应.改变控制器结构后,无论控制器结构变为方系统、 瘦系统还是胖系统,其操作变量的个数都没有改变.如果能够保证在系统稳定以后,输入变量稳态值能够达到系统正常时与设定点相对应的值,那就意味着在变结构控制器下系统在稳定时能达到与原来一样的状态,没有被控制器采样的输出最终也会达到原来的控制要求.为了使输入变量的稳态值能够达到本文所期望的值,需要在式(3)中添加对输入变量稳态值的跟踪:
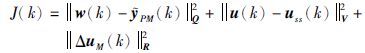
|
(9) |
其中,u(k)为控制输入预测值,u(k)=u(k-1)+BΔuM(k),
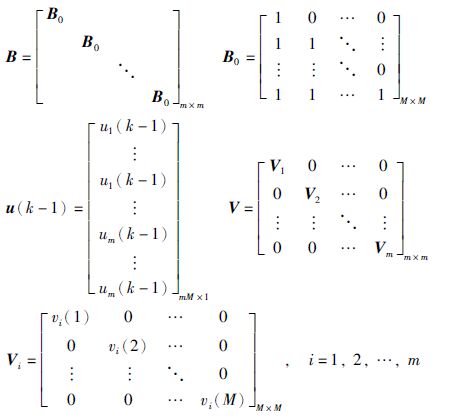
|
将式(2)代入式(9),可得
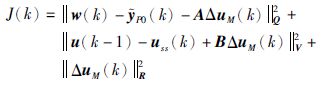
|
(10) |
根据极值必要条件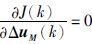
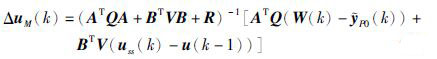
|
(11) |
使用式(10)求解控制增量,需要在控制器中设定输入变量的稳态目标uss(k).尤其在控制器结构为胖系统的情形下,给定的设定点存在不唯一的稳态输入值,使用对输入变量稳态值跟踪的控制律,对原系统中设定点对应的操作变量稳态值进行跟踪,使变结构控制达到与故障前一样的控制目标.
4.4 变结构控制实施流程根据上文中的分析,给出面向输入输出故障的变结构预测控制方法实施流程.流程图见图 3,具体步骤如下:
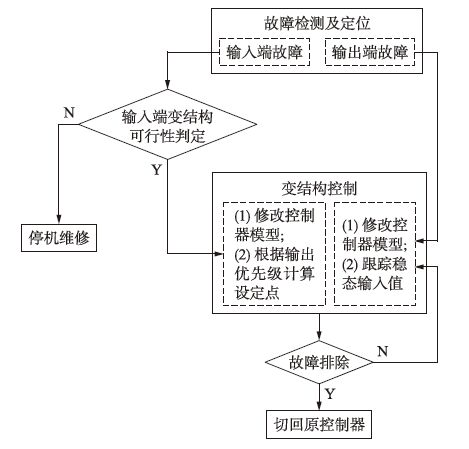
|
| 图 3 变结构控制实施流程 Figure 3 Procedure of variable structure control |
步骤1 故障检测及定位.确定故障来自于输入变量还是输出变量.如果故障为输入端故障,转步骤2; 如果故障为输出端故障,转步骤3.
步骤2 输入端变结构控制可行性判定.可行性指改变控制器结构后能否一定满足重要输出可达.假设故障输入个数为l,原控制器操作变量个数为m,变结构后控制器操作变量个数将是m-l,若必须要满足设定要求的输出个数p′≤m-l,则可进行变结构控制,转步骤3; 否则应该采取其它措施.对于输出端故障的情况,不需要进行可行性判定.
步骤3 修改控制器模型进行变结构控制.根据已定位的故障输入或者输出,选择原控制器模型中与故障输入或输出无关的子模型作为新的控制器模型,具体见4.2小节及4.3小节.针对输入端故障,根据输出优先级和稳态模型计算新的设定点.针对输出端故障,对未发生故障时设定点对应的稳态输入值进行跟踪.
步骤4 故障排除后退出变结构控制,使用原控制器.
5 仿真验证依旧采用Shell benchmark问题的重油分馏塔模型,来验证DMC变结构控制的有效性.上文已经分别模拟了输入端执行机构失效和输出端存在很大采样噪声这两种故障,本节将针对这两类故障,采用变结构的方式进行仿真验证.式(3)所示模型的稳态增益矩阵为
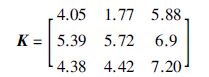
|
(12) |
采用DMC算法,输出目标设为y=[0.5,-0.5,0.5]T,Q、 R均取单位阵,预测时域P=120,控制时域M=20,系统初始状态为零,故省略所有稳态计算中的增量符号Δ.达到稳态后输入稳态值为u=[-0.578 5,-0.198 7,0.543 3]T.
5.1 输入端变结构控制仿真图 1所示故障情形下,第3路输入的故障导致了系统不能达到原来的设定点,系统稳定后,y=[0.240 1,-0.756 8,-0.544 9]T,u=[-0.199 2,-0.320 8,0]T.
将第3路输入从控制器的操作变量中去除,此时控制器结构由方系统变为瘦系统,控制器模型和对应的稳态增益矩阵为
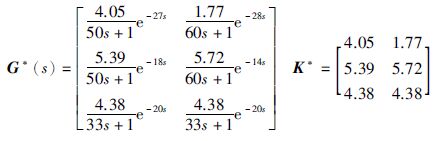
|
假定第3路输出的优先级最低,根据式(7)有:
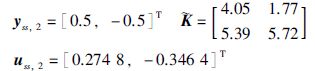
|
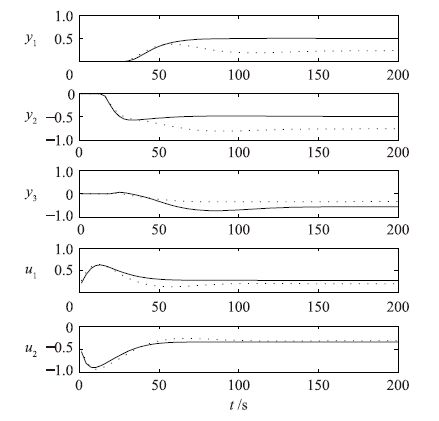
根据式(8)得yss,3=[0.499 8,-0.500 2,-0.327 5]T为新的设定点,仿真结果见图 4,其中点线代表输入存在故障时系统的变化,实线为变结构控制下系统的变化.
|
| 图 4 输入端变结构控制仿真 Figure 4 Simulation of variable structure control on input |
系统达到稳态时y=[0.500 1,-0.498 7,-0.329 2]T,u=[0.274 9,-0.347 1]T.在改变控制器结构以后,优先级较高的y1和y2基本达到了原来的设定要求,但同时牺牲了优先级最低的y3的控制目标.为方便对比,变结构控制前后的稳态值在表 1中罗列.
| u1 | u2 | u3 | y1 | y2 | y3 | |
| 无故障时的输入输出稳态值 | 0.578 5 | 0.198 7 | 0.543 3 | 0.5 | -0.5 | 0.5 |
| 输入故障时输入输出稳态值 | 0.199 2 | 0.320 8 | 0.0 | 0.240 1 | -0.756 8 | -0.544 9 |
| 输入故障时变结构控制稳态值 | 0.279 4 | 0.347 1 | 0.0 | 0.500 1 | -0.498 7 | -0.329 2 |
| 输出故障变结构无输入稳态值跟踪 | 0.666 0 | 0.415 5 | -0.248 8 | 0.500 0 | -0.500 0 | -0.710 3 |
| 输出故障变结构有输入稳态值跟踪 | 0.575 1 | 0.199 2 | 0.541 0 | 0.499 9 | -0.499 9 | 0.496 5 |
对于图 2所示的输出端故障情形,假设已定位故障发生在第3路输出,则将第3路输出从控制器的被控输出变量中去除,控制器结构由方系统变为胖系统,控制器模型为:
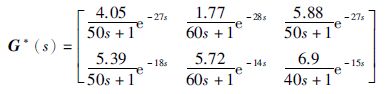
|
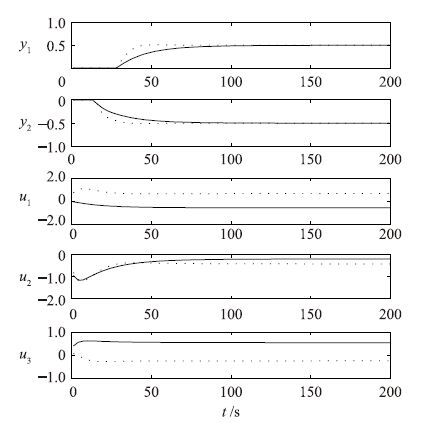
考虑到胖系统输入稳态值不唯一,使用包含输入变量稳态值跟踪的DMC算法,仿真结果见图 5.
|
| 图 5 输出端变结构控制仿真 Figure 5 Simulation of variable structure control on output |
图 5中点线表示没有对输入变量稳态值进行跟踪的结果,实线表示对输入变量稳态值跟踪的结果.输入稳态值与输出稳态值的对比见表 1(表 1同时列出了y3,y3是被控对象实际的输出值,只是没有被控制器采样).
仿真结果验证了对于输出端故障的变结构控制的有效性.结合对输入变量稳态值进行跟踪的DMC算法,未被控制器包含在内的输出变量也基本达到了原控制目标,但其动态过程是没有经过控制器优化的,超调量较大.
图 6中实线是传感器故障的输出端y3在未包含输入变量稳态值跟踪的DMC算法下的实际变化曲线,其余3条虚线分别代表了y3在包含输入变量稳态值跟踪的DMC算法下,不同控制权矩阵系数所对应的结果,此处将控制权矩阵表示为R=rI.增大控制权矩阵可以降低超调量,但会增加过程的调节时间和上升时间.当r从1变到50时,y1的调节时间增加19步,上升时间增加15步; y2的调节增加21步,上升时间增加20步.故在控制器参数的选择上需要权衡未被控制器包含在内的输出的超调量与其它输出的响应速度.
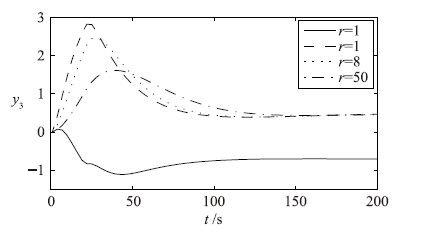
|
| 图 6 传感器故障输出端的实际变化 Figure 6 The actual change of output with sensor fault |
对于输入端故障情形,当采用变结构控制方法降低控制器操作变量自由度使得系统变为瘦系统时,控制目标往往难以实现,通过选择优先级较高的输出变量来重新计算设定点,可以实现优先级较高的输出目标可达,可优先选择的输出变量个数与变结构后操作变量的个数相同.对于输出端故障的情形,变结构控制减少被控输出变量的个数,采用结合输入变量稳态值跟踪的DMC算法,使系统稳态时输入稳态值达到与原设定值对应的值,从而使得未被控制器包括在内的输出也达到原控制要求.
本文所提出的变结构控制方法在保障主要控制目标的同时,也有相应的代价.如,对于输入端故障处理的结果是完全牺牲了较低优先级的输出变量的控制目标,输出变量优先级的确定需要权衡各方面因素; 对于输出端故障的处理,可能导致从控制器结构中去除的那些输出变量的过程动态性能下降,调整控制权矩阵来获得改善的同时又会影响其它输出的动态性能.这些问题是下一步改进和研究的方向.
| [1] | Richalet J, Rault A, Testud J L. Model predictive heuristic control:Applications to industrial processes[J]. Automatica, 1978, 14 (5): 413–428. DOI:10.1016/0005-1098(78)90001-8 |
| [2] | Culter C R, Yocum F H. Experience with the DMC inverse for identification[C]//Proceedings of the 4th International Conference on Chemical Process Control. 1991:297-317. |
| [3] | Clarke D W, Mohtadi C, Tuffs P S. Generalized predictive control, part 2:Extensions and interpretations[J]. Automatica, 1987, 23 (2): 149–160. DOI:10.1016/0005-1098(87)90088-4 |
| [4] | 席裕庚. 预测控制[M]. 北京: 国防工业出版社 ,2013 : 51 -72. Xi Y G. Predictive Control[M]. 2nd ed. Beijing: National Defense Industry Press , 2013 : 51 -72. |
| [5] | Darby M L, Nikolaou M. MPC:Current practice and challenges[J]. Control Engineering Practice, 2012, 20 (4): 328–342. DOI:10.1016/j.conengprac.2011.12.004 |
| [6] | Neshasteriz A R, Khaki-Sedigh A, Sadjadian H. Generalized predictive control and tuning of industrial processes with second order plus dead time models[J]. Journal of Process Control, 2010, 20 (1): 63–72. DOI:10.1016/j.jprocont.2009.10.003 |
| [7] | 钱积新, 赵均, 徐祖华. 预测控制[M]. 北京: 化学工业出版社 ,2007 : 2 -16. Qian J X, Zhao J, Xu Z H. Predictive control[M]. Beijing: Chemical Industry Press , 2007 : 2 -16. |
| [8] | 席裕庚, 李德伟, 林姝. 模型预测控制——现状与挑战[J]. 自动化学报, 2013, 39 (3): 222–236. Xi Y G, Li D W, Lin S. Model predictive control-Status and challenges[J]. Acta Automatica Sinica, 2013, 39 (3): 222–236. DOI:10.1016/S1874-1029(13)60024-5 |
| [9] | 杜运成, 石红瑞, 杨晓波. 控制系统故障诊断方法综述[J]. 工业仪表与自动化装置, 2008 (5): 9–13. Du Y C, Shi H R, Yang X B. Asurvey of fault diagnosis methods in control systems[J]. Industrial Instrumentation & Automation, 2008 (5): 9–13. |
| [10] | Pranatyasto T N, Qin S J. Sensor validation and process fault diagnosis for FCC units under MPC feedback[J]. Control Engineering Practice, 2001, 9 (8): 877–888. DOI:10.1016/S0967-0661(01)00055-7 |
| [11] | Qin S J, Li W. Detection and identification of faulty sensors in dynamic processes[J]. Aiche Journal, 2001, 47 (7): 1581–1593. DOI:10.1002/(ISSN)1547-5905 |
| [12] | 李俊领, 杨光红. 自适应容错控制的发展与展望[J]. 控制与决策, 2014, 29 (11): 1921–1926. Li J L, Yang G H. Development and prospect of adaptive fault-tolerant control[J]. Control and Decision, 2014, 29 (11): 1921–1926. |
| [13] | Chen W, Jiang J. Fault-tolerant control against stuck actuator faults[J]. IEE Proceedings-Control Theory Applications, 2005, 152 (2): 138–146. DOI:10.1049/ip-cta:20041231 |
| [14] | 高闪, 梅劲松. 输入非线性系统的执行器故障容错控制[J]. 信息与控制, 2015, 44 (4): 463–468. Gao S, Mei J S. Fault tolerant control of actuator faults for input nonlinear systems[J]. Information and Control, 2015, 44 (4): 463–468. |
| [15] | Xu Z H, Zhu Y C, Han K, et al. A multi-iteration pseudo-linear regression method and adaptive disturbance model for MPC[J]. Journal of Process Control, 2010, 20 (4): 384–395. DOI:10.1016/j.jprocont.2010.02.004 |
| [16] | 金鑫, 池清华, 刘康玲, 等. 对角CARIMA模型抗扰约束广义预测控制[J]. 化工学报, 2014, 65 (4): 1310–1316. Jin X, Chi Q H, Liu K L, et al. Disturbance rejection constraints generalized predictive control of diagonal CARIMA model[J]. CIESC Journal, 2014, 65 (4): 1310–1316. |
| [17] | 邹涛, 丁宝苍, 张端. 模型预测控制工程应用导论[M]. 北京: 化学工业出版社 ,2010 : 115 -128. Zou T, Ding B C, Zhang D. MPC:An introduction to industrial application[M]. Beijing: Chemical Industrial Press , 2010 : 115 -128. |
| [18] | 王文博, 赵均, 徐祖华. 扰动自适应模型预测控制的频域特性分析[J]. 计算机与应用化学, 2011, 28 (12): 1492–1496. Wang W B, Zhao J, Xu Z H. Frequency behavior analysis for predictive control with adaptive disturbance model[J]. Computers and Applied Chemistry, 2011, 28 (12): 1492–1496. |
| [19] | 李少远. 工业过程系统的预测控制[J]. 控制工程, 2010, 17 (4): 407–415. Li S Y. Model-based predictive control for industrial process-A survey[J]. Control Engineering of China, 2010, 17 (4): 407–415. |
| [20] | 邹涛, 李海强, 丁宝苍, 等. 多变量预测控制系统稳态解的相容性与唯一性分析[J]. 自动化学报, 2013, 39 (5): 519–529. Zou T, Li H Q, Ding B C, et al. Compatibility and uniqueness analysis of steady state solution for multi-variable predictive control system[J]. Acta Automatica Sinica, 2013, 39 (5): 519–529. |



