2. 天津大学机器人与自主系统研究所, 天津 300072;
3. 天津市过程检测与控制重点实验室, 天津 300072
2. The Institute of Robotics and Autonomous System, Tianjin University, Tianjin 300072, China;
3. The Tianjin Key Laboratory of Process Measurement and Control, Tianjin 300072, China
1 引言
工业革命之后,越来越多的自动控制装置,如机械手、 数控机床等,解放了手工劳动力,大大地方便了工业生产.自动控制系统是这类控制装置的核心,控制系统性能的好坏较大程度上决定了工业产品的质量,所以对这些系统实施精确控制就显得尤为重要.然而由于这些被控对象大多是多输入多输出的非线性系统,具有多个运动自由度,包含时变、 非线性、 强耦合等动力学特征,用常规的控制方法很难达到高精度的控制要求.
在众多非线性控制策略中,滑模变结构控制(sliding mode variable structure control,SMVSC)方法作为一种经典的鲁棒控制方法[1-2],具有结构简单、 响应快、 鲁棒性强的优点,是一种较为成熟的控制策略.目前,滑模控制有大量的研究成果,如终端滑模控制[3-5]、 自适应滑模控制[6-7]、 离散滑模控制[8]、 神经网络滑模控制[9]等.
传统的滑模控制方法虽然性能优良,但也存在着一些缺陷.由于控制律中存在不连续的符号函数切换项,使得控制输入产生抖振现象[10].在实际应用中,抖振现象可能产生高频响应,造成系统不稳定,也会导致执行器损坏,极大地限制了滑模控制方法的广泛应用.文[11]使用饱和函数代替符号函数,使控制输入连续,有效地削弱了抖振,但由于系统状态将不会沿着滑模面运动,因此将导致控制精度和鲁棒性降低.另外,滑模控制中控制增益的选取需要对系统不确定性的上界有一个先验的估计[12].若控制增益选取过小,将会丧失控制能力,导致系统不稳定; 控制增益选取过大,将会带来较大的抖振,浪费了控制能量,也将影响控制精度.
针对滑模控制的抖振问题,可采用以下解决办法:
(1) 使用饱和函数代替符号函数[11],使控制输入连续,有效削弱了抖振,但由于系统状态将不会沿着滑模面运动,因此将导致控制精度和鲁棒性降低.
(2) 采用2阶滑模控制方法.2阶滑模控制最早由Levant在文[13]中提出,可以削弱1阶滑模控制中的抖振问题,其将不连续的控制输入作用在滑模面的2阶导数上,使得实际控制信号为不连续反馈控制的积分,最终得到连续平滑的控制输入.文[14]针对非线性系统的控制问题设计了两种2阶滑模控制算法,实现了闭环系统的全局有限时间稳定性和抖振削弱性能.文[15]设计了自适应Super-Twisting滑模控制算法,在系统扰动上界未知的条件下实现控制,并通过实验验证了算法的有效性.文[16]将2阶滑模控制算法应用于了倒立摆的控制中.
为了解决上文提到的关于传统滑模控制的诸多缺陷,使滑模控制能更好地应用于实际控制系统中,本文基于本课题组自行设计开发的一套3自由度多变量控制实验平台展开理论和实验研究,设计了一种新型的自适应2阶终端滑模控制策略.该控制方案保留了滑模控制结构简单、 鲁棒性强的优点,并有效削弱了滑模控制引发的抖振问题.具体来说,该控制器采用非线性终端滑模面取代传统线性滑模面,在控制输入的时间导数中加入不连续的滑模切换项,经过积分后得到真实的控制输入,减小了控制器的抖振.为了使该控制器对于外界扰动有较强的鲁棒性,设计了自适应控制增益,使控制器能够根据外界扰动动态地调节控制增益,并且不需要外界扰动的先验信息,使控制器更加灵活实用.通过李亚普诺夫稳定性理论分析证明了闭环系统的稳定性及所设计的控制器能够实现控制误差的有限时间收敛.为了验证所设计算法的有效性,使用本课题组自行设计开发的3自由度控制实验平台进行了实验验证.实验结果表明,所设计的新型滑模控制律可以实现真实系统的控制.
2 平台介绍本研究组自主设计的3自由度多变量控制实验平台[17]如图 1所示.该实验平台将小型无人直升机约束在球头上,并一同固定在支撑杆的一端,另一端连接在固定底座之上,使得被控对象仅仅可以进行俯仰、 滚转及偏航三个自由度的运动.通过球头的约束能力,俯仰角和滚转角最大偏角为15°.该平台基于MATLAB RTW工具箱的xPC目标实时仿真环境,采用自主设计的基于ARM Cortex-M3内核的惯性测量单元作为传感器提供三轴姿态角和角速度信息,测量精度为俯仰角和滚转角0.2°、 偏航角0.5°.该实验平台主要分为控制器模块、 控制信号执行模块及数据采集三部分构成.控制器模块主要利用参考姿态轨迹信号与反馈获得的实时状态信息,执行控制算法并输出控制信号; 控制信号执行模块借助于串口通信模块,将控制信号发送给底层DSP电路板,进行十字盘解耦运算,得到舵机的执行信号; 数据采集模块主要完成姿态的数据读取与处理.整个硬件在环仿真系统控制频率为500 Hz.

|
| 图 1 3自由度控制实验平台 Figure 1 Three degrees of freedom control experimental platform |
该3自由度被控对象是一个多输入多输出的被控系统,为了方便控制,可以近似将其看作一个刚体,利用拉格朗日方程来描述其动力学模型,具体描述为
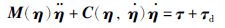
|
(1) |
式中,η=[φ,θ,ψ]T为姿态角向量,φ为滚转角,θ为俯仰角,ψ为偏航角; M(η)∈R3×3为可逆的惯性矩阵; 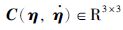
控制目标为设计力矩控制输入τ∈R3×1使得3轴姿态角η=[φ,θ,ψ]T跟踪目标姿态角轨迹ηd=[φd,θd,ψd]T,并且确保所有的闭环信号都是有界的.这里假定目标轨迹ηd∈L∞,其1阶、 2阶、 3阶时间导数存在并且${{\dot{\eta }}_{\text{d,}}}{{\ddot{\eta }}_{\text{d}}},{{\eta }_{\text{d}}}\text{=}{{L}_{\infty }}$.
3.2 开环误差系统构建定义控制误差为
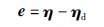
|
(2) |
对式(2)两端同时求3阶时间导数,并将式(1)代入整理得到:
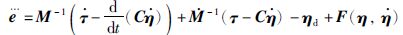
|
(3) |
式中,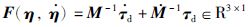
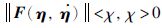
设计线性滑模面s=[s1,s2,s3T∈R3×1为
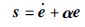
|
(4) |
式中,α=diag(α1,α2,α3)且满足α1,α2,α3>0.对式(4)两端同时求1阶和2阶时间导数得到:
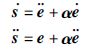
|
(5) |
设计终端滑模面[18-19] σ=[σ1,σ2,σ3]T∈R3×1为
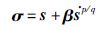
|
(6) |
式中,β=diag(β1,β2,β3)满足β1,β2,β3>0,p和q为正奇数且满足1<p/q<2.对式(6)两端同时求1阶时间导数,得到:
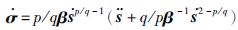
|
(7) |
设计控制输入转矩τ为
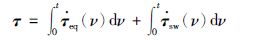
|
(8) |
式中,${{{\dot{\tau }}}_{\text{eq}}}$为等效控制输入,${{{\dot{\tau }}}_{\text{sw}}}$为切换控制输入,ν为积分变量.${{{\dot{\tau }}}_{\text{eq}}}$和${{{\dot{\tau }}}_{\text{sw}}}$设计如下:
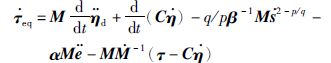
|
(9) |
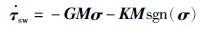
|
(10) |
式中,G=diag(g1,g2,g3)为固定控制器增益矩阵,K=diag(k1,k2,k3)为自适应控制器增益矩阵.将式(8)~式(10)代入式(7)后得到闭环误差动力学方程:
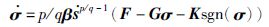
|
(11) |
设计滚转、 俯仰和偏航通道的自适应控制增益k1、 k2、 k3的更新律${{{\dot{k}}}_{i}}$为:
当|σi|≠0时,${{{\dot{k}}}_{i}}$为
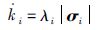
|
(12) |
式(12)中λi为自适应更新速率,满足λi>0,i=1,2,3.并假设自适应控制增益ki的初值ki(0)>0,i=1,2,3.
当|σi|=0时,ki为
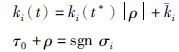
|
(13) |
式(13)中参数${{{\dot{k}}}_{i}}$决定了控制增益ki(t)的最小值,ρ为辅助变量,τ0为设定的时间常数.t*代表滑模面从|σi|≠0状态到|σi|=0状态的切换时刻,即σi(t*-)≠0,σi(t*)=0,t*-代表t*的前一时刻.
该自适应律的工作过程为: 假设初始时刻|σi|≠0,控制增益将会依照式(12)的自适应律增大,直到控制增益足以抵消外界扰动使得滑模面收敛到|σi|=0,这时控制增益会依照式(13)下降,直到外界扰动发生变化使得控制增益下降后不足以抵消扰动.之后控制增益又会按照式(12)的自适应律增大,如此往复,自适应增益总是处于一个动态的变化过程中.
4 稳定性分析定理1 对于式(1)的非线性系统,设计非线性终端滑模面σ的误差动力学方程为式(7),设计控制输入为式(8)~(10),自适应控制增益为式(12)和式(13),则存在一个有限时间tF≥0,使得滑模面σ对于任意t>tF都有:
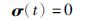
|
(14) |
引理1 对于滑模面σ的闭环动力学方程式(11),设计控制增益自适应律式(12)、 式(13),则自适应控制增益向量K(t)=[k1(t),k2(t),k3(t)]T存在上界,即存在一个常数向量K*=[k1*,k2*,k3*]T(k1*,k2*,k3*>0)使得
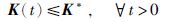
|
(15) |
证明 此定理的证明可以分为以下两种情况来讨论:
情形1 当|σ(t)|≠0时,给出引理1.定义自适应控制增益的误差向量为K(t)-K*=[k1(t)-k1*,k2(t)-k2*,k3(t)-k3*]T.选取非负李亚普诺夫候选函数为
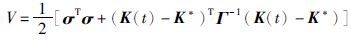
|
(16) |
其中Γ-1=diag(γ1-1,γ2-1,γ3-1),γ1-1,γ2-1,γ3-1>0.对式(16)两边同时求1阶时间导数可得
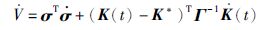
|
(17) |
将式(11)和式(12)代入式(17)可得
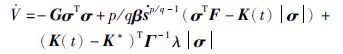
|
(18) |
由引理1可知对任意t>0总存在K*>0使得K(t)≤K*,将式(18)整理后得
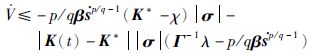
|
(19) |
在式(19)中,令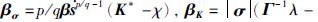
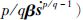
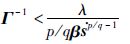
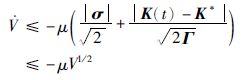
|
(20) |
式中,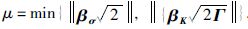
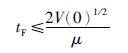
|
(21) |
情形2 当σ(t)=0时,由文[20]中的定理1可得,若自适应增益K(t)足以抵消系统的不确定性,则依照式(17)的自适应律,系统的滑模面将保持在σ(t)=0.因此当σ(t)=0时,满足文[20]中定理1的条件,滑模面将保持σ(t)=0.
定理1得证.
引理1证明 假设初始状态σ(t)≠0,系统不确定性χ有界,则由式(12)的自适应律可以得出自适应增益K(t)将增长.假设达到时刻t1时满足K(t1)>χ.由此可知K(t)已足够大使得滑模面收敛,设t2时刻滑模面收敛,即σ(t)=0,则K(t2)必然是有界的,之后自适应增益K(t)将按照式(13)的规律下降.因此总存在一个正数K*使得对所有t>0都有K(t)<K*.引理1得证.
5 实验验证为验证上述控制律设计的有效性,体现工程实用价值.本文利用本研究组自主设计的3自由度多变量控制实验平台,进行了实时的镇定和跟踪飞行实验.
5.1 姿态镇定控制实验进行姿态镇定控制实验时设置给定的姿态参考信号为ηd(t)=[0°,0°,0°]T.在实验过程中,首先由操作人员手动起飞无人直升机,然后通过遥控器中的一路切换通道改为自动飞行状态.小型无人直升机利用本文所提出的控制器,切换后保持悬停状态自主飞行.在50 s时刻由外界加入风速为3 m/s~5 m/s的横向阵风干扰直到实验结束,测试被控对象的抗风鲁棒性能.进行姿态镇定实验时设置相关控制器参数为表 1所示.实验结果如图 2~图 4所示.
| 控制器参数 | 取值 |
| α | diag(65,65,10) |
| p | 5 |
| q | 3 |
| β | diag(0.1,0.1,0.01) |
| G | diag(5,5,0.001) |
| λ | [0.1,0.1,0.000 15]T |
| K | [0.1,0.1,0.000 01]T |

|
| 图 2 镇定实验: 姿态角 Figure 2 Stabilization experiment: Attitudes |
|
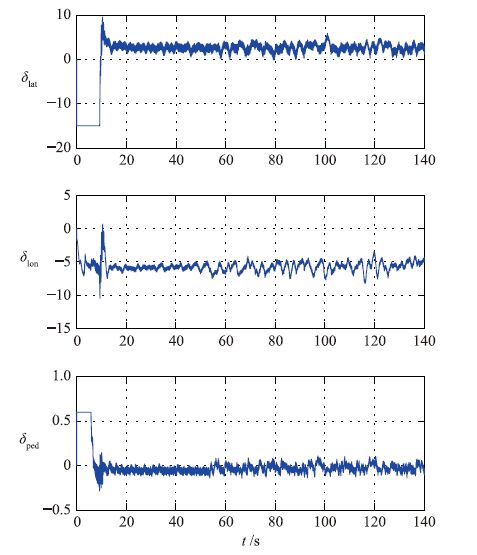
| 图 3 镇定实验: 控制输入 Figure 3 Stabilization experiment: Control inputs |
|
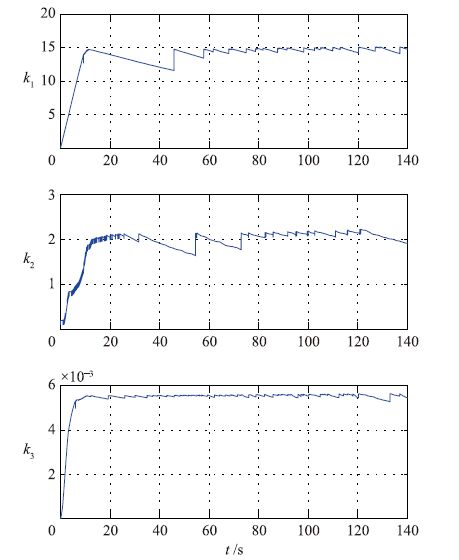
| 图 4 镇定实验: 自适应增益 Figure 4 Stabilization experiment: Adaptive control gains |
图 2为被控对象姿态角变化曲线,由图可知在无风悬停时姿态角的调节时间在5 s以内,滚转角和俯仰角控制精度保持在1°以内,偏航角控制精度保持在2°以内.加入阵风干扰后,控制器仍能使被控对象保持稳定悬停状态,滚转角和俯仰角控制精度保持在1.5°以内,偏航角控制精度保持在2°以内.从图 3和图 4可以看出,控制输入及自适应控制增益均稳定在一定范围内.该实验结果验证了本文所提出的控制器的合理性.
5.2 姿态跟踪控制实验进行姿态跟踪控制实验时设定给定的姿态参考为ηd(t)=[8°sin(0.1πt),8°cos(0.1πt),0°]T.控制器参数的设置与镇定实验相同,采用论文中提出的控制器,由悬停状态下在30 s处加入设定的姿态参考轨迹,当切换到自动控制时,滚转和俯仰通道分别跟踪幅值为8°的正弦和余弦信号,偏航保持镇定.从效果上看,直升机将做一个画圆的动作.实际飞行数据如图 5~图 8所示.
|
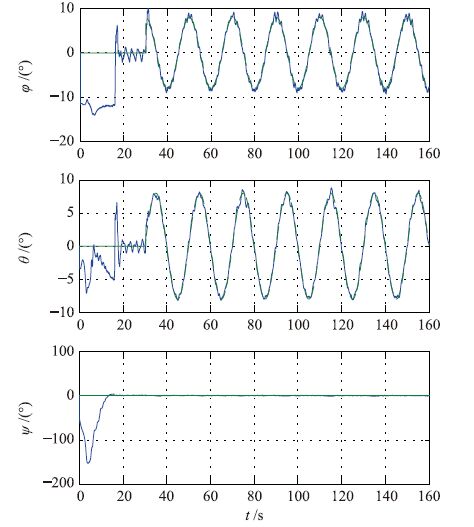
| 图 5 姿态跟踪实验: 姿态角 Figure 5 Attitude tracking experiments: Attitudes |
|
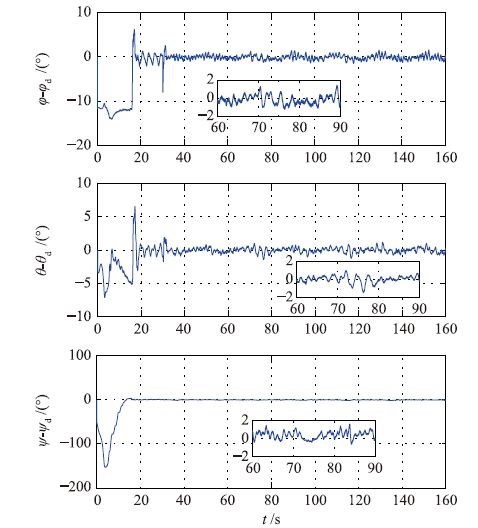
| 图 6 姿态跟踪实验: 姿态角误差 Figure 6 Attitude tracking experiments: Attitudes tracking errors |

|
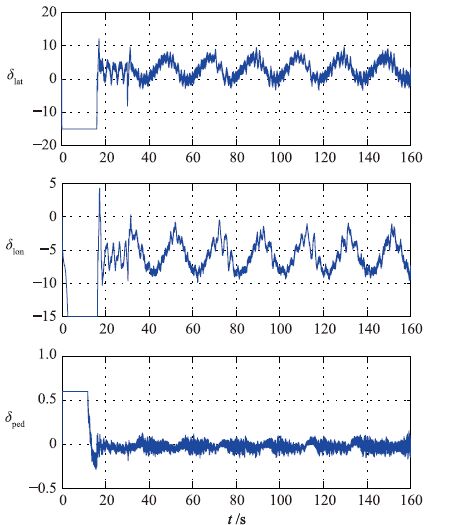
| 图 7 姿态跟踪实验: 控制输入 Figure 7 Attitude tracking experiment: Control inputs |
|
| 图 8 姿态跟踪实验: 自适应增益控制 Figure 8 Attitude tracking experiments: Adaptive control gains |
由图 5和图 6可知,实验取得良好的跟踪效果,滚转角及俯仰角跟踪控制精度为1.5°,偏航角控制精度为2°.图 7为控制输入变化曲线,图 8为自适应控制增益变化曲线.控制输入及自适应控制增益均稳定在一定范围内.
本文作者尝试了用传统的滑模控制律应用到该实验平台中进行控制实验,以作为该新型控制算法的对照.但是由于滑模控制的带来的抖振现象以及控制参数调整困难使得实验失败,被控对象在振颤之后不能保持稳定,控制信号发散.由此可见该控制算法相对于传统滑模控制算法的优越性.
6 结论本文针对一类非线性多变量被控对象的控制问题,设计了一种基于自适应2阶终端滑模的自主控制方法.通过理论分析与实验验证表明: (1) 该控制算法可以实现闭环系统的稳定性以及控制误差的有限时间收敛,有效削弱了传统滑模控制引发的抖振问题.(2) 该控制算法应用于真实的3自由度控制系统时,取得了良好的姿态镇定和跟踪控制性能,各个参数均稳定在一定范围内.
| [1] | 刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24 (3): 407–418. Liu J K, Sun F C. Research and development on theory and algorithms of sliding mode control[J]. Control Theory and Applications, 2007, 24 (3): 407–418. |
| [2] | 夏元清, 付梦印, 邓志红, 等. 滑模控制和自抗扰控制的研究进展[J]. 控制理论与应用, 2013, 30 (2): 137–147. Xia Y Q, Fu M Y, Deng Z H, et al. Recent developments in sliding mode control and active disturbance rejection control[J]. Control Theory and Applications, 2013, 30 (2): 137–147. |
| [3] | Zhao D Y, Zou T. A finite-time approach to formation control of multiple mobile robots with terminal sliding mode[J]. International Journal of Systems Science, 2012, 43 (11): 1998–2014. DOI:10.1080/00207721.2011.564323 |
| [4] | Zhao D, Li S, Zhu Q. Output feedback terminal sliding mode control for a class of second order nonlinear systems[J]. Asian Journal of Control, 2013, 15 (1): 237–247. DOI:10.1002/asjc.v15.1 |
| [5] | Li S, Zhou M, Yu X. Design and implementation of terminal sliding mode control method for PMSM speed regulation system[J]. IEEE Transactions on Industrial Informatics, 2013, 9 (4): 1879–1891. DOI:10.1109/TII.2012.2226896 |
| [6] | Mahmoud M S, Boukas E, Ismail A. Robust adaptive control of uncertain discrete-time state-delay systems[J]. Computers and Mathematics with Applications, 2008, 54 (12): 2887–2908. |
| [7] | Plestan F, Shtessel Y, Bregeault V, et al. New methodologies for adaptive sliding mode control[J]. International Journal of Control, 2010, 83 (9): 1907–1919. DOI:10.1080/00207179.2010.501385 |
| [8] | Chen X K. Adaptive sliding mode control for discrete-time multi-input multi-output systems[J]. Automatica, 2006, 42 (3): 427–435. DOI:10.1016/j.automatica.2005.10.008 |
| [9] | Parma G G, Menezes B R, Braga A P, et al. Sliding mode neural network control of an induction motor drive[J]. International Journal of Adaptive Control and Signal Processing, 2003, 17 (6): 501–508. DOI:10.1002/(ISSN)1099-1115 |
| [10] | Fridman L M. An averaging approach to chattering[J]. IEEE Transactions on Automatic Control, 2001, 46 (8): 1260–1265. DOI:10.1109/9.940930 |
| [11] | Chung S C Y, Lin C L. A transformed lure problem for sliding mode control and chattering reduction[J]. IEEE Transactions on Automatic Control, 1999, 44 (3): 563–568. DOI:10.1109/9.751351 |
| [12] | Slotine J J E, Sastry S S. Tracking control of non-linear systems using sliding surface, with application to robot manipulators[J]. International Journal of Control, 1983, 38 (2): 465–492. DOI:10.1080/00207178308933088 |
| [13] | Levant A. Sliding-order and sliding accuracy in sliding mode control[J]. International Journal of Control, 1993, 58 (6): 1247–1263. DOI:10.1080/00207179308923053 |
| [14] | Ding S, Wang J, Zheng W X. Second-order sliding mode control for nonlinear uncertain systems bounded by positive functions[J]. IEEE Transactions on Industrial Electronics, 2015, 62 (9): 5899–5909. DOI:10.1109/TIE.2015.2448064 |
| [15] | Shtessel Y, Taleb M, Plestan F. A novel adaptive-gain supertwisting sliding mode controller:Methodology and application[J]. Automatica, 2012, 48 (48): 759–769. |
| [16] | 李雪冰, 马莉, 丁世宏. 一类新的二阶滑模控制方法及其在倒立摆控制中的应用[J]. 自动化学报, 2015, 41 (1): 193–202. Li X B, Ma L, Ding S H. A new second-order sliding mode control and its application to inverted pendulum[J]. Acta Automatica Sinica, 2015, 41 (1): 193–202. |
| [17] | 鲜斌, 古训, 刘祥, 等. 小型无人直升机姿态非线性鲁棒控制设计[J]. 控制理论与应用, 2014, 31 (4): 409–416. Xian B, Gu X, Li uX, et al. Nonlinear robust attitude control for a miniature unmanned helicopter[J]. Control Theory and Applications, 2014, 31 (4): 409–416. |
| [18] | Xu S D, Chen C C, Wu Z L. Study of nonsingular fast terminal sliding-mode fault-tolerant control[J]. IEEE Transactions on Industrial Electronics, 2015, 62 (6): 1–1. |
| [19] | Feng Y, Yu X, Man Z. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38 (12): 2159–2167. DOI:10.1016/S0005-1098(02)00147-4 |
| [20] | Lee H, Utkin V I. Chattering suppression methods in sliding mode control systems[J]. Annual Reviews in Control, 2007, 31 (2): 179–188. DOI:10.1016/j.arcontrol.2007.08.001 |



