1 引言
永磁同步电动机具有气隙磁密高、 转矩/惯量比大、 效率高、 结构简单等优点,以永磁同步电动机为执行电机的交流调速系统已成为电气传动系统发展的一个主流方向,在电动汽车、 电梯、 数控机床、 家用电器等应用领域已获得广泛应用.但电机在运行过程中,由于随着内部环境(如温度)的变化导致电机参数的不稳定,当在某些特定参数条件下工作时,电机会产生混沌现象,出现一系列不规则运动,具体表现为转速、 转矩的不规则振荡和一系列不规则噪声,严重影响系统运行的高效性与稳定性.因此,需要抑制PMSM在运行过程中的混沌现象.
永磁同步电动机调速系统通常采用速度传感器获取速度和转子位置信息(如编码器、 旋转变压器等),它是控制系统脆弱的一环,易受电磁噪声和恶劣环境的影响.当出现故障时,常常导致系统飞车,损坏设备,甚至对操作者的人身安全产生威胁.无速度传感器控制方法可减小安装体积、 节约成本、 提高系统可靠性,将其应用到PMSM控制系统中已成为交流调速的一个重要方向.
Hemati首次发现了开环系统PMSM的混沌现象,随后
文[1]利用李亚普诺夫指数和容量维分析了永磁同步电机的混沌现象.针对永磁同步电机混沌控制问题,典型的控制方法有纳入轨道与强迫迁徙控制方法[2]、 线性反馈控制方法[3]、 延迟反馈控制方法[4]、 微分几何方法[5]、 无源控制方法[6-7]、 自适应模糊控制方法[8]等.这些控制方法大多是在系统参数确定且不受外界扰动影响的情况下对永磁同步电机混沌现象进行控制.近年来,一些学者将鲁棒性较强的非线性控制方法应用到永磁同步电机混沌控制中.文[9]利用滑模变结构控制原理,将含有扰动的系统混沌轨道先后控制到任意固定点和周期轨道.文[10]设计了针对永磁同步电机混沌现象的自抗扰控制器(ADRC)对电机运行过程中出现的混沌现象进行控制.文[11]针对部分状态不可测的永磁同步电机混沌系统,结合自适应滑模控制和扩张状态观测器理论,提出了基于扩张状态观测器的永磁同步电机自适应混沌控制方法.但这些方法对永磁同步电机混沌运动控制基本上都是停留在理论数学模型基础上的,没有拓展到矢量控制系统中.
本文在无速度传感器PMSM矢量控制调速系统基础上,采用非奇异快速终端滑模控制的方法来抑制PMSM在运行过程中出现的混沌现象.利用扩张状态观测器估计转速,构成无速度传感器PMSM矢量控制系统,在此基础上设计非奇异快速终端滑模控制器.无速度传感器调速系统运行时速度环开始采用传统PI(proportional-integral)调节器,永磁同步电机正常运行,在运行过程中,由于随着内部环境(如温度)的变化导致电机参数的不稳定,在某些参数和工作条件下产生混沌现象,即刻通过非奇异快速终端滑模控制器取代传统PI调节器,从而抑制PMSM的混沌现象.仿真结果表明该方法是有效的.
2 永磁同步电机的混沌模型永磁同步电机在d-q旋转坐标系下的数学模型可表示为
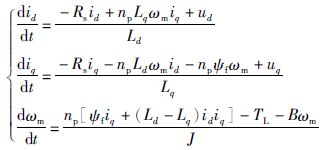
|
(1) |
式中,id、 iq分别为电机d轴和q轴的电流分量,Ld、 Lq分别为d轴和q轴的电感,ud、 uq分别为电机d轴和q轴的电压分量,ωm为电机的转速,Rs为定子电阻,J为电机的转动惯性系数,B为电机的粘滞阻尼系数,ψf为永磁体磁链,TL为负载转矩,np为电机极对数.
假设永磁同步电机气隙均匀(Ld=Lq=L),通过仿射变换x=λ和时间尺度变换t=τ,永磁同步电机数学模型转化为混沌模型的无量纲状态方程为
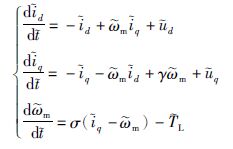
|
(2) |
式中,

电机在运行过程中,随着内部环境的变化(比如温度),电机的内部参数也会随着变化,当电机参数如表 1时,取σ=5.46,γ=20,采用矢量控制策略,永磁同步电机会出现混沌现象,id、 iq、 ωm三维相图响应曲线如图 1所示.
| 参数 | 数值 |
| d、 q轴电感Ld=Lq | 14.25 mH |
| 定子电阻Rs | 0.9 Ω |
| 永磁体磁链ψf | 0.031 Wb |
| 转动惯量J | 4.7×10-5 kg·m2 |
| 粘滞阻尼系数B | 0.016 2 N·m·s |
| 极对数np | 4 |

|
| 图 1 id、 iq、 ωm的三维相图 Figure 1 Three dimensional phase graph of id、 iq、 ωm |
从图 1可以看出,PMSM产生洛仑兹混沌吸引子,出现了混沌运动现象.
3 扩张状态观测器的速度估计自抗扰控制器(ADRC)是一种不依赖系统模型的非线性控制技术,能够对系统运行时的各种扰动实时进行估计和补偿,并结合非线性反馈达到好的控制性能.扩张状态观测器是自抗扰控制器的其中一部分,是一种优于普通状态观测器的器件,它把有未知外扰的非线性不确定对象用非线性状态反馈化为积分串联型,并在反馈中加以补偿.这样被扩张的状态对未知扰动的实时作用量就能得到很好的估计,它对一定范围的对象具有很好的适应性和鲁棒性,从而提高了系统的控制性能[12].本文利用PMSM数学模型中的运动方程,不论是传统的数学模型(1)还是混沌模型(2),都可将运动方程写成ESO的标准形式:

|
(3) |
其中a(t)看作系统的“综合扰动项”,利用ESO可以准确地将其观测出来[13].因此可构造出PMSM的非线性扩张状态观测器为

|
(4) |
其中,z1用来估计速度ωm或

|
β1、 β2为输出误差校正增益,Fal函数为最优综合控制函数,δ为滤波因子,α为非线性因子.该观测器既适用于常规状态时的速度观测,也同样适用于电机混沌状态的速度观测.扩张状态观测器(ESO)仿真原理图如图 2所示.

|
| 图 2 扩张状态观测器(ESO)仿真原理图 Figure 2 Simulation principle diagram of ESO |
本文采用非奇异快速终端滑模控制策略实现外环的转速控制,使滑模控制系统具有全局快速收敛性[14-20],从而抑制电机混沌运动.取PMSM系统的状态变量为

|
(5) |
式中,
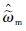
设计非奇异快速终端滑模面:
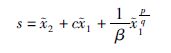
|
(6) |
式中,c∈R+,β∈R+,p,q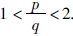
为抑制滑模抖振问题,保证非奇异性,采用一种带终端吸引子的趋近方式设计趋近律:
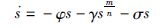
|
(7) |
式中,φ∈R+,γ∈R+,m,n∈N为奇数且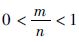
定理 对转速误差系统式(5),如果选取非奇异快速终端滑模面式(6)并设计式(7)的趋近律,使其满足式(11),则电机转速将在有限时间内趋于稳定.
证明 根据式(2)、 式(5),认为
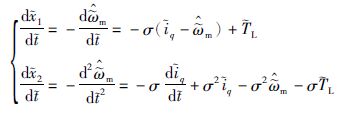
|
(8) |
由式(6)作为系统滑模面,并对s求导得

|
(9) |
由此可推出:
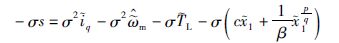
|
(10) |
由式(7)、 式(9)、 式(10)得出PMSM非奇异快速终端滑模速度控制器:

|
(11) |
选择李亚普诺夫函数为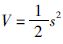

|
(12) |
式中,

为了验证所设计的控制器在无速度传感器调速系统中抑制电机混沌运动的效果,在Simulink环境下搭建模型进行仿真研究.采用的永磁同步电动机原始运行参数如表 2所示.
| 参数 | 数值 |
| d、 q轴电感Ld=Lq | 8.5×10-3 H |
| 定子电阻Rs | 2.875 0 Ω |
| 永磁体磁链ψf | 0.175 Wb |
| 转动惯量J | 0.000 8 kg·m2 |
| 粘滞阻尼系数B | 0.001 N·m·s |
| 极对数np | 4 |
无速度传感器永磁同步电机混沌运动的非奇异快速终端滑模控制系统原理图如图 3所示.

|
| 图 3 无速度传感器永磁同步电机混沌运动控制系统原理图 Figure 3 Schematic diagram of chaotic motion control system for speed sensorless PMSM |
给定转速ωm*=300 rad/s,速度外环开始是传统PI调节器,t=0 s时系统开始启动并稳定运行.由于实际运行过程中,永磁同步电动机受系统环境(如温度)影响,其内部参数是不稳定的,当t=0.2 s时永磁同步电动机内部参数发生变化,当达到某些参数和工作条件时,具体见表 1.此时永磁同步电动机进入混沌运动状态,出现了转速、 转矩的不规则振荡和一系列不规则噪声.当t=0.2 s时加入控制器,即用不非奇异快速终端滑模控制器取代传统PI调节器,控制器参数取为p=9,q=7,m=3,n=5,c=50,β=0.01,φ=100,γ=2.仿真结果如图 4~图 6所示.

|
| 图 4 id响应曲线 Figure 4 Response curve of id |
|
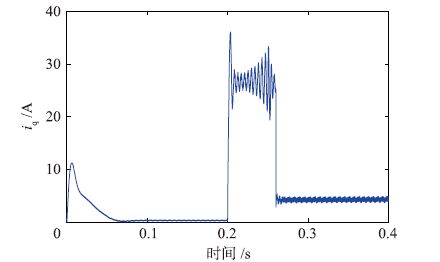
| 图 5 iq响应曲线 Figure 5 Response curve of iq |

|
| 图 6 实际/估计转速响应曲线 Figure 6 Curves of actual/estimated speed response |
从图 6中可以看出,电机从t=0 s开始正常运行; 运行一段时间后,当t=0.2 s时进入混沌运动状态; 当t=0.25 s时加入控制器后,电机很快脱离了混沌运动状态.估计的转速不受电机参数的影响始终迅速准确地跟踪上期望转速,实际的转速在0.2 s~0.25 s内规则振荡,电机进入混沌运动状态,控制器切入后电机很快脱离了混沌运动; 另外交轴电流iq和直轴电流id两个状态变量,在加入控制器后也迅速脱离了混沌运动状态.
6 结论本文提出了利用扩张状态观测器估计转速和非奇异快速终端滑模控制抑制电机混沌运动的控制方法.该方法可以迅速、 有效地抑制PMSM中的混沌现象,估计的转速不受电机参数的影响始终迅速准确地跟踪上期望转速,可以保证电机运行的稳定性和可靠性,算法实现简单,过程容易实现.因此,后续工作将进一步完善与拓展此类方法,并进行实验验证.该方法可为其它非线性控制方法的混沌抑制应用提供参考.
| [1] | 张波, 毛宗源. 利用Lyapunov指数和容量维分析永磁同步电机仿真中的混沌现象[J]. 控制理论与应用, 2001, 18 (4): 589–596. Zhang B, Mao Z Y. Analyzing chaotic phenomenon in permanent-magnet synchronous motors with Lyapunov exponent and capacity dimension[J]. Control Theory & Applications, 2001, 18 (4): 589–596. |
| [2] | 李忠, 张波, 毛宗源. 永磁同步电机系统的纳入轨道和强迫迁徙控制[J]. 控制理论与应用, 2001, 11 (1): 53–56. Li Z, Zhang B, Mao Z Y. Entrainment and migration control of permanent magnet synchronous motor System[J]. Control Theory & Applications, 2001, 11 (1): 53–56. |
| [3] | 王兴元, 段朝锋. 用线性反馈方法实现不确定Lorenz系统混沌控制[J]. 大连理工大学学报, 2005, 45 (6): 892–896. Wang X Y, Duan C F. Chaos controlling of uncertain Lorenz system using linear feedback[J]. Journal of Dalian University of Technology, 2005, 45 (6): 892–896. |
| [4] | 任海鹏, 刘丁, 李洁. 永磁同步电机中混动运动的延迟反馈控制[J]. 中国电机工程学报, 2003, 23 (6): 175–178. Ren H P, Liu D, Li J. Delay feedback control of chaos in permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2003, 23 (6): 175–178. |
| [5] | 韦笃取, 罗晓曙, 方锦清. 基于微分几何方法的永磁同步电机的混沌运动的控制[J]. 物理学报, 2006, 55 (1): 54–59. Wei D Q, Luo X S, Fang J Q. Controlling chaos in permanent magnet synchronous motor based on the differential geometry method[J]. Acta Physica Sinica, 2006, 55 (1): 54–59. |
| [6] | 吴忠强, 谭拂晓. 永磁同步电动机混沌系统的无源化控制[J]. 中国电机工程学报, 2006, 26 (18): 159–163. Wu Z Q, Tan F X. passivity control of permanent-magnet synchronous motors chaotic system[J]. Proceedings of the CSEE, 2006, 26 (18): 159–163. |
| [7] | 马国进, 齐冬莲, 赵光宙. 无源性理论在永磁同步电动机混沌控制中的应用[J]. 电路与系统学报, 2004, 9 (5): 91–94. Ma G J, Qi D L, Zhao G Z. Control of permanent magnet synchronous motor chaotic phenomena based on passive network theory[J]. Journal of Circuits and Systems, 2004, 9 (5): 91–94. |
| [8] | Yu J P, Chen B, Yu H S. Adaptive fuzzy tracking control for the chaotic permanent magnet synchronous motor drive system via backstepping[J]. Nonlinear Analysis:Real World Applications, 2011, 12 (1): 671–681. DOI:10.1016/j.nonrwa.2010.07.009 |
| [9] | 杨晓辉, 刘小平, 柳和生. 基于滑模变结构永磁同步电机混沌跟踪控制[J]. 电源技术, 2014, 38 (12): 2331–2335. Yang X H, Liu X P, Liu H S. Chaos tracking control of permanent magnet synchronous motor based on sliding mode[J]. Chinese Journal of Power Sources, 2014, 38 (12): 2331–2335. |
| [10] | 李峰磊, 贾亚飞, 刘福才. 永磁同步电机中混沌运动的自抗扰控制[J]. 控制工程, 2013, 20 (s0): 129–132. Li F L, Jia Y F, Liu F C. Active disturbance rejection control of chaos in permanent magnet synchronous motor[J]. Control Engineering of China, 2013, 20 (s0): 129–132. |
| [11] | 陈强, 南余荣, 邢科新. 基于扩张状态观测器的永磁同步电机混沌系统自适应滑模控制[J]. 物理学报, 2014, 63 (22): 220506–1. Chen Q, Nan Y R, Xing K X. Adaptive sliding-mode control of chaotic permanent magnet synchronous motor system based on extended state observer[J]. Acta Physica Sinica, 2014, 63 (22): 220506–1. |
| [12] | 邵立伟, 廖晓钟. 自抗扰控制在永磁同步电机无速度传感器调速系统的应用[J]. 电工技术学报, 2006, 21 (6): 35–39. Shao L W, Liao X Z. Application of active disturbance rejection controller and extend state observer for PMSM[J]. Transactions of China Electrotechnical Society, 2006, 21 (6): 35–39. |
| [13] | 侯利民, 王巍. 无速度传感器的表面式永磁同步电机无源控制策略[J]. 控制与决策, 2013, 28 (10): 1578–1586. Hou L M, Wang W. Speed sensorless system of passivity-based control strategy for SPMSM[J]. Control and Decision, 2013, 28 (10): 1578–1586. |
| [14] | Shao X D, Zhu L K, Liu Y Q. SMDO-based backstepping terminal sliding mode control method for hot press hydraulic position servo system[C]//27th Chinese Control and Decision Conference. Piscataway, NJ, USA:IEEE, 2015:596-601. |
| [15] | 周硕, 王大志, 高庆忠. 永磁同步电机非奇异快速终端滑模控制[J]. 电气传动, 2014, 44 (1): 51–54. Zhou S, Wang D Z, Gao Q Z. Nonsingular fast terminal-sliding-mode control for permanent magnet synchronous motor[J]. Electric Drive, 2014, 44 (1): 51–54. |
| [16] | 张晓光, 赵克, 孙力. 永磁同步电机混合非奇异终端滑模变结构控制[J]. 中国电机工程学报, 2011, 31 (27): 116–122. Zhang X G, Zhao K, Sun L. Hybrid nonsingular terminal sliding mode control for permanent magnet synchronous motor drive system[J]. Proceedings of the CSEE, 2011, 31 (27): 116–122. |
| [17] | 侯利民, 王巍. 表面式永磁同步电机无源非奇异快速终端滑模控制[J]. 电工技术学报, 2014, 29 (11): 45–52. Hou L M, Wang W. Passivity-based control and nonsingular fast terminal sliding mode control for SPMSM[J]. Transactions of China Electrotechnical Society, 2014, 29 (11): 45–52. |
| [18] | 阎晓妹, 尚婷, 赵小国. 基于主动滑模控制的不确定分数阶混沌(超混沌)系统的延迟同步[J]. 信息与控制, 2015, 44 (1): 1–7. Yan X M, Shang T, Zhao X G. Lag synchronization of uncertain fractional-order chaotic (hyperchaotic) systems using active sliding mode control[J]. Information and Control, 2015, 44 (1): 1–7. |
| [19] | Ginoya D, Shendge P D, Phadke S B. Sliding mode control for mismatched uncertain systems using an extended disturbance observer[J]. IEEE Transactions on Industrial Electronics, 2014, 61 (4): 1983–1992. DOI:10.1109/TIE.2013.2271597 |
| [20] | Zhang X G, Sun L Z, Zhao K. Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques[J]. IEEE Transactions on Power Electronic, 2013, 28 (3): 1358–1365. DOI:10.1109/TPEL.2012.2206610 |



