2. 武警工程大学研究生管理大队, 陕西 西安 710078
2. Graduate Management Team, Engineering University of Armed Police Force, Xi'an 710078, China
1 引言
交—交变换器是一种常见的电力电子器件,它包括传统交—交型和矩阵式交—交型两种型式,传统交—交型仅需一次换流就能实现变频且能量可双向流通,但使用的晶闸管多且输入功率因数(power factor,PF)低,因而限制了其使用场合.为了提高交—交型变换器性能和扩大应用范围,矩阵变换器(matrix converter,MC)应运而生.
作为一种新型交—交型变频器,MC具有一系列优点: 实现电能的双向流动、输入电流和输出电压为正弦波、可任意调整输入侧PF、无中间直流储能环节、体积小、结构紧凑及谐波污染小等,因此,MC已成为交—交变频研究热点,并在电机驱动领域受到了国内外研究者的重视[1-5].
永磁同步电机(permanent magnet synchronous motor,PMSM)具有转矩惯量比高、体积小和高功率因数等优点,因而在中小功率变频调速领域应用非常广泛.对于PMSM驱动系统而言,目前成熟的控制方法有磁场定向控制(field oriented control,FOC)和直接转矩控制(direct torque control,DTC).基于定子电流控制方式的FOC,其固有电流内环的存在影响了驱动系统响应性能,相比较而言,基于开关表的DTC省去了坐标变换,具有快速系统响应的特点,因而在工业界得到了广泛应用.
目前PMSM的DTC控制系统中外环转速调节器一般采用PI.在一定条件下PI能起调节作用,但电机参数变化或存在外部负载扰动时,这种线性调节器难以保证系统获得满意性能.为了改善速度调节器的鲁棒性,一些先进控制方法相继被提出[6-10].文[6]提出了基于滑模(slide mode,SM)的速度调节器,该调节器使系统具有快速性和鲁棒性,但SM变结构带来的系统高频颤振现象是不可避免的.文[10]首次提出自抗扰控制技术(active disturbance rejection control,ADRC),其突出特征就是把作用于被控对象的所有不确定因素归结为“未知扰动”,而用对象的输入和输出数据对它进行估计并给予补偿[11-12],ADRC不依赖于系统精确数学模型,具有很强的鲁棒性和实用性[13-15],且采用非线性函数fal(·)的ADRC能够避免SM的缺点.因此,本文PMSM的DTC系统的外环速度调节器将用ADRC替代PI.
近年来,国内外学者对MC在电机调速中的应用做了大量的研究工作.文[16]对MC驱动PMSM控制系统的矢量控制进行了实验研究,给出了MC的调制方法,设计了电流补偿环节,改善了转矩脉动.文[17]提出了一种新的MC驱动感应电机DTC方法,用滑模变结构控制器替代转矩环和磁链环的滞环比较器,从而实现MC开关频率恒定,减小了转矩脉动.文[18]对MC驱动PMSM系统的开关周期占空比时间进行优化,并改进了MC的DTC开关表,提出了一种新的DTC方法,有效地降低了转矩脉动,消除了低转速下的定子磁链畸变.文[19]为了提高针对输入电压非正常情况下系统的抗扰动能力,用ADRC取代PI速度调节器,研究了MC驱动的感应电机FOC方法,该方法首次将ADRC和MC相结合进行控制电机研究,基于该方法的优点,引发了本文将其应用到PMSM控制中的思路.
针对PMSM系统,考虑到抗干扰要求、快速的动态响应和较少的超调量要求、输入电流和输出电压为正弦波要求、输入侧PF能够达到1的要求等,本文提出了基于ADRC的MC驱动的DTC控制方法.
2 矩阵变换器驱动永磁同步电机系统数学模型 2.1 矩阵变换器拓扑结构及其数学模型MC多采用三相—三相形式,它包括3×3共9个双向开关,每一个开关具有双向导通和关断的能力.MC输入侧为三相电压源,输出侧为三相PMSM,其原理如图 1所示.
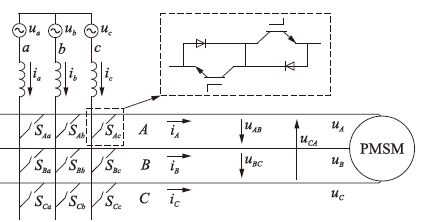
|
| 图 1 矩阵变换器拓扑 Figure 1 The topology of matrix converter |
MC输入侧电压Ui、电流Ii和输出侧电压Uo、电流Io的关系可以表示为
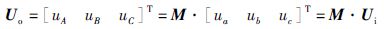
|
(1) |
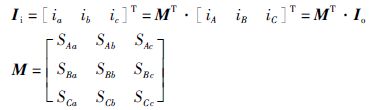
|
(2) |
式(1)和式(2)中: Smn(m∈{A,B,C},n∈{a,b,c})为MC中开关状态,Smn=1和Smn=0分别表示导通和关断; M为MC输入侧至输出侧的传递函数矩阵.
MC在工作中遵循输入侧任意两相间不能短路、输出侧任意一相电路不能断路的原则,因此,可以得到以下关系:
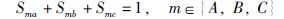
|
(3) |
根据式(3)的约束条件,MC可调制出27种开关状态,其中用于DTC的开关状态共有21种.因此,MC比传统电压源逆变器输出更多的电压矢量,从而获得更好的控制效果.基于MC的DTC系统不仅可以控制转矩和定子磁链,而且还可以控制输入侧PF.为了便于对输入侧PF控制和输出侧DTC的研究,可将MC等效为图 2所示的虚拟交—直变换器和虚拟直—交变换器两部分.
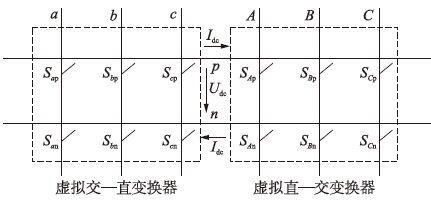
|
| 图 2 矩阵变换器的等效交—直—交结构 Figure 2 Equivalent AC-DC-AC structure of matrix converter |
采用面贴式PMSM,其定子电流和定子磁链方程在α、β两相静止坐标系下可表示为
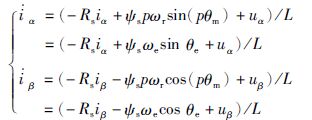
|
(4) |
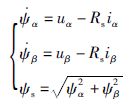
|
(5) |
式(4)和式(5)中,iα、iβ、uα、uβ、ψα、ψβ分别为定子电流、定子电压、定子磁链在α、β轴的分量; ψs为永磁体磁链,Rs为定子电阻,L为定子绕组电感,ωr、ωe为转子的机械角速度和电气角速度; θm和θm为转子的机械角位移和电气角位移,p为极对数.
PMSM机械转动方程为
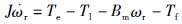
|
(6) |
式中,J为转动惯量,Tl为负载转矩,Bm为粘滞摩擦系数,Tf为库伦摩擦转矩,Te为电磁转矩,在α、β两相静止坐标系下可以表达为
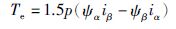
|
(7) |
针对MC驱动PMSM系统,基于ADRC速度调节器DTC系统如图 3所示.研究的核心问题就是通过选择MC输入侧电流矢量和MC输出侧电压矢量,从而控制MC的开关状态,以实现PMSM系统的DTC.图 3中系统主要设计任务包括ADRC速度调节器设计和MC驱动PMSM的DTC设计.

|
| 图 3 基于ADRC速度调节器的MC驱动PMSM的DTC原理图 Figure 3 Schematic diagram of DTC for PMSM driven by MC based on speed regulator of ADRC |
图 4是基于ADRC的速度调节器结构图,它由扩张状态观测器(extended state observer,ESO)和非线性状态误差反馈控制律(nonlinear state error feedback,NLSEF)组成,通过ESO对系统状态和扰动进行估计,利用NLSEF实现对扰动补偿.
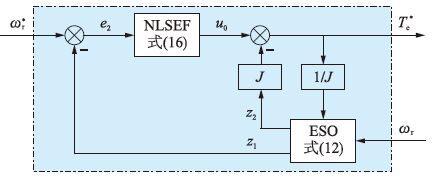
|
| 图 4 基于ADRC的速度调节器结构图 Figure 4 Structure of ADRC-based speed regulator |
令:
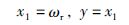
|
系统(6)的一阶状态空间方程为
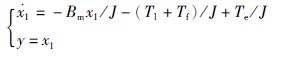
|
(8) |
式中,转速y和电磁转矩Te分别为输出和输入.
由式(8)可知,PMSM在实时控制中会受到负载转矩变化的外部干扰、库仑摩擦转矩和粘滞摩擦系数等参数变化的内部干扰,从而对电机动态性能带来负面影响.将上述各种干扰作用的总效果用未知的不确定函数f(t)表示,即:
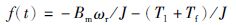
|
(9) |
将f(t)扩张为一个新状态变量x2,即x2=f(t),令:
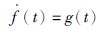
|
(10) |
则式(8)可扩张为下面的二阶状态空间方程:
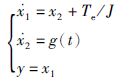
|
(11) |
式(11)是能观的,因此其相应二阶ESO数学模型为
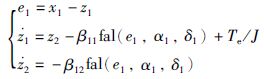
|
(12) |
式中,z1为y的跟踪信号,z2为系统总干扰估计值,α1为非线性因子,δ1为滤波因子,β11和β12为误差反馈增益, fal(·)为非线性函数,其定义为
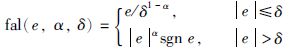
|
(13) |
式中,0<α<1,δ>0.
根据文[20],选择适当的δ1、α1、β11和β12,可保证扩张状态观测器(12)快速逼近系统(11)状态x1和总干扰f(t).
3.1.2 扰动信号的抑制采用图 4所示的NLSEF对估计出的总干扰f(t)进行补偿.NLSEF定义为
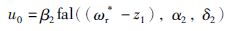
|
(14) |
因此,基于ADRC的速度调节器输出为
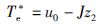
|
(15) |
式中,Te*是提供给图 3所示DTC的参考电磁转矩.
说明:
(1) ESO和NLSEF中采用的非线性函数fal(·)是具有线性段的连续的幂次函数,α<1时,它具有“小误差大增益、大误差小增益”的特性,能够减少系统稳态误差、改善动态性能、提高扰动抑制能力,同时避免系统产生稳态高频抖振[21].
(2) ESO参数选取的一般原则如下[20, 22-23]:
1) 关于αi(i=1,2),选取为0.5,使得fal(·)中幂次函数变为整数次开方,从而降低计算量.
2) 关于δi(i=1,2),表示原点附近线性区间宽度,与系统误差范围有关,一般取0.000 1≤δi≤1(i=1,2).当δi取值小于0.002 5时容易导致高频脉动,而δi取值过大时则起不到非线性反馈控制效果,因此实际应用中一般取为0.01左右.
3) 关于β11和β12,根据跟踪性能确定.β11和β12取较大值有利于提高ESO跟踪速度,但将导致振荡及超调现象.通常情况下,β12的取值比β11大1~2个数量级.
3.2 MC驱动PMSM的DTC由图 3可知,MC驱动PMSM的DTC系统由3部分组成: 虚拟交—直变换器控制、虚拟直—交变换器控制及MC开关选择.
3.2.1 虚拟直—交变换器输出电压矢量选择虚拟直—交变换器的控制采用传统电压源逆变器DTC策略,即根据式(5)和式(7)计算出定子磁链ψs和转矩Te,将给定转矩Te*和磁链ψs*分别与实际转矩Te和磁链ψs进行比较,其误差经过滞环比较器输出τ和ψ,再结合定子磁链所在扇区Nl(l=1,…,6)来选择相应的输出电压矢量.
虚拟直—交变换器共有8种开关组合,相应产生8个电压矢量,其表达式为
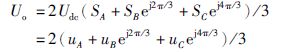
|
(16) |
式中,Udc是图 2中虚拟直—交变换器的输入直流电压; Si(i=A,B,C)为第i桥臂功率开关管状态,Si=1表示上桥臂导通,Si=-1表示下桥臂导通.
根据式(16),虚拟直—交变换器的输出电压矢量共有8个,即Uo∈{U0,U1,U2,U3,U4,U5,U6,U7},其中,U0和U7为2个零矢量,U1~U6是6个非零矢量,其分布如图 5所示,N1~N6是相平面的6个扇区.
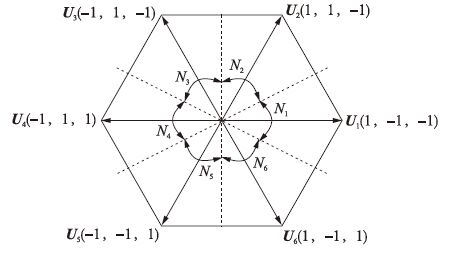
|
| 图 5 虚拟直—交变换器的输出电压矢量 Figure 5 Output voltage vector of virtual DC-AC converter |
虚拟直—交变换器输出电压矢量根据DTC原理来选择.
3.2.2 虚拟交—直变换器输入电流矢量选择MC输入侧电压矢量就是电源的电压矢量,它以固定频率旋转而不受MC开关状态影响,而输入电流矢量则受MC开关状态影响,其相位可控.这就为输入电流矢量选择提供了依据.
虚拟交—直变换器的控制原理: 比较输入电压矢量相位θiu与输入电流矢量相位θii,它们的相位差Δθ通过图 3所示的相位滞环比较器输出δ,再结合输入电压矢量所在扇区Ml(l=1,…,6)来选择输入电流矢量,控制目标就是减小Δθ,从而使输入电压矢量与输入电流矢量的相位一致,也就是使得输入侧的PF为1.
虚拟交—直变换器的输入电流矢量表达式为
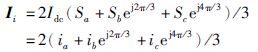
|
(17) |
式中,Idc是图 2中虚拟交—直变换器的输出直流电流; Si(i=a,b,c)为第i桥臂功率开关管状态,Si=1表示上桥臂导通,Si=-1表示下桥臂导通,Si=0表示上下桥臂均不导通.根据式(17),变换器的输入电流矢量共有9个,即Ii∈{I1,I2,I3,I4,I5,I6,I7,I8,I9},其中,I7~I9为3个零矢量,I1~I6是6个非零矢量,其分布如图 6所示,M1~M6是相平面的6个扇区.
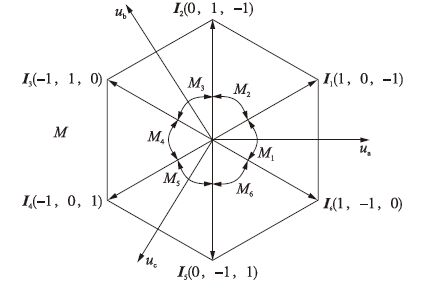
|
| 图 6 虚拟交—直变换器的输入电流矢量 Figure 6 Input current vector of virtual AC-DC converter 中文注解 |
图 3中相位滞环比较器定义为
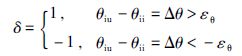
|
(18) |
式中,εθ是相位滞环比较器误差界限.
根据使输入电压矢量与输入电流矢量同相位的控制目标,可以得到表 1所示的虚拟交—直变换器输入电压矢量选择表.
| δ | Ml | |||||
| M1 | M2 | M3 | M4 | M5 | M6 | |
| 1 | I1 | I2 | I3 | I4 | I5 | I6 |
| -1 | I6 | I1 | I2 | I3 | I4 | I5 |
MC开关状态是由虚拟整流侧和虚拟逆变侧的开关状态共同决定的.虚拟交—直开关状态取决于输入电流矢量的选择,虚拟直—交变换器开关状态取决于输出电压矢量的选择,因此,结合输入电流矢量选择和输出电压矢量选择,可以得到表 3所示MC的开关状态选择表.
表 2中“acc”表示: 当虚拟逆变侧的输出电压矢量为U1、虚拟整流侧的输入电流矢量为I1时,则MC中的SAa,SBc,SCc 3个开关导通(即,MC输出A、B、C分别与输入a、c、c相连).以此类推,可以解释表 3中的其他符号表示的开关组合.
| Ii | Uo | |||||||
| U1 | U2 | U3 | U4 | U5 | U6 | U0 | U7 | |
| I1 | acc | aac | cac | caa | cca | aca | ccc | aaa |
| I2 | bcc | bbc | cbc | cbb | ccb | bcb | ccc | bbb |
| I3 | baa | bba | aba | abb | aab | bab | aaa | bbb |
| I4 | caa | cca | aca | acc | aac | cac | aaa | ccc |
| I5 | cbb | ccb | bcb | bcc | bbc | cbc | bbb | ccc |
| I6 | abb | aab | bab | baa | bba | aba | bbb | aaa |
为了验证本文所提设计方法的有效性和正确性,采用Matlab进行了仿真研究.所用PMSM电机参数为[24]: 定子电阻Rs=2.875 Ω,额定功率PN=1.1 kW,额定转速ωn=3 000 rad/min,额定转矩Tn=3 N·m,定子等效电感L=0.008 5 H,永磁体磁势ψs=0.175 Wb,转动惯量J=8×10-4 kg·m2,库仑摩擦转矩Tf=0 N·m,粘滞摩擦系数Bm=0 N·m·s,极对数p=4.
为了验证所设计系统的输入侧PF为1和鲁棒性,给出了2种仿真研究方案:
(1) 对基于ADRC速度调节器MC驱动PMSM的DTC系统,将输入侧相电压和相电流的相位进行比较;
(2) 针对基于PI、基于SM和基于ADRC的速度调节器MC驱动PMSM的3个DTC系统,就负载和给定转速变化情况进行比较分析.
仿真中系统三相交流输入电压为220 V、频率为50 Hz,采样周期为10 μs.上述2种仿真研究方案中涉及的ADRC采用同样参数,其参数设置为: β11=950,β12=6 500,β2=15,α1=α2=0.5,δ1=δ2=0.01.
基于SM的速度调节器,本文采用指数趋近律,其控制输出为
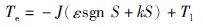
|
SM速度调节器详细设计过程见附录.
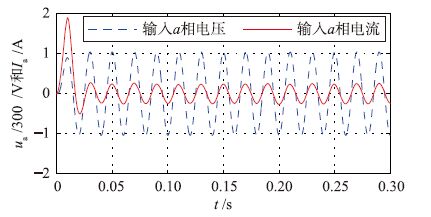
4.1 MC输入电压与输入电流的相位比较仿真时启动给定转速为1 000 rad/min,PMSM带载(1 N·m)启动.由于输入电压幅值比输入电流幅值大很多,为了将它们表示在同一坐标下,故将实际输入电压缩小300倍.图 7给出了输入侧a相电流和缩小300倍的a相电压.
|
| 图 7 a相输入电压和a相输入电流 Figure 7 Input voltage and input current of phase a |
由图 7可以看出,MC输入电流与输入电压同相位,即输入侧PF能够达到1且输入电流波形基本为正弦波.
4.2 基于PI、基于SM与基于ADRC的系统抗扰动能力比较为了进行合理地比较,调节PI和SM速度调节器参数,使得基于PI、滑模和ADRC的3个DTC PMSM系统启动时尽可能具有同样暂态响应特性(即,转速响应均无超调且具有同样调节时间),此时PI参数取值为: kp=0.3,ki=0.22; SM参数取值为: ε=100,k=400.
4.2.1 系统抗负载变化能力比较仿真时启动给定转速为1 000 rad/min,PMSM带载(1 N·m)启动,在0.1 s时加载到2 N·m.
图 8、图 9和图 10是分别采用PI、SM和ADRC速度调节器时的系统仿真结果(包括转速和转矩).
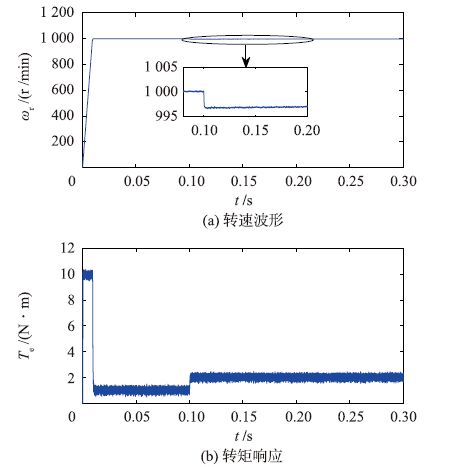
|
| 图 8 负载转矩变化时采用PI速度调节器的系统响应 Figure 8 The system response of PI speed regulator in the case of load torque change |
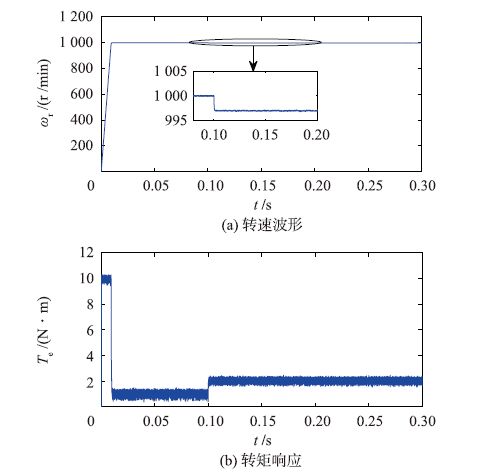
|
| 图 9 负载转矩变化时采用SM速度调节器系统动态响应 Figure 9 The system dynamic responses of based-SM speed regulator in the case of load torque change |
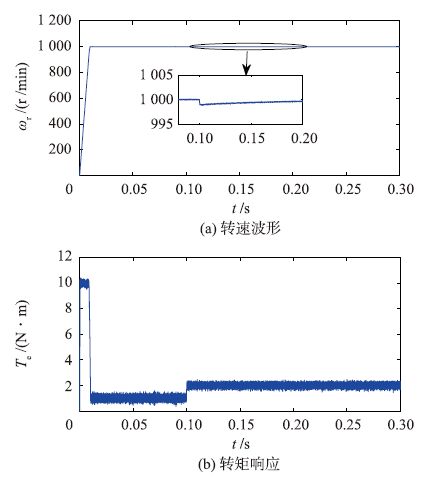
|
| 图 10 负载转矩变化时采用ADRC速度调节器的系统响应 Figure 10 The system response of ADRC speed regulator in the case of load torque change |
通过比较图 8、图 9和图 10可以看出,当负载转矩变化时,采用PI和SM速度调节器的两个系统,其转速降落较大,恢复到稳态值所需时间较长; 而采用ADRC速度调节器的系统,其转速下降少,恢复到稳态值所需时间较短.因此,采用ADRC的系统比采用PI和SM的系统抗负载扰动能力更强.
4.2.2 系统跟踪给定转速变化的能力比较仿真时PMSM带载1 N·m启动,启动给定转速为1 000 rad/min,在0.1 s时突升至1 200 rad/min,在0.2 s时突降至900 rad/min.
图 11、图 12和图 13是分别采用PI、SM和ADRC速度调节器时的系统仿真结果(包括转速和转矩).
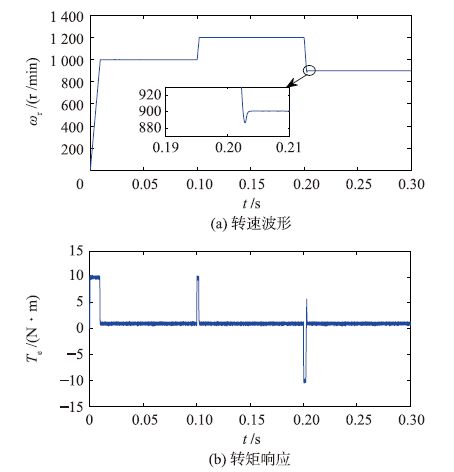
|
| 图 11 转速变化时采用PI速度调节器的系统动态响应 Figure 11 The system dynamic responses of PI-based speed regulator in the case of motor speed change |
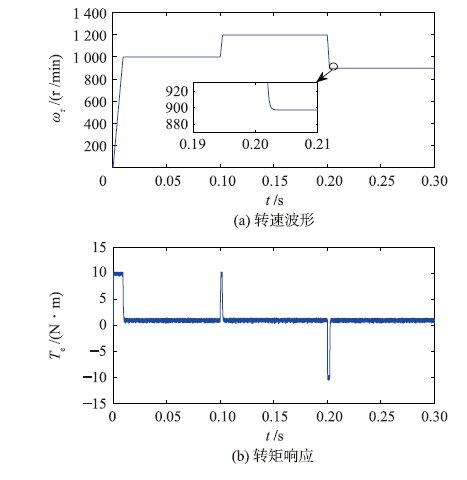
|
| 图 12 转速变化时采用SM速度调节器的系统动态响应 Figure 12 The system dynamic responses of based-SM speed regulator in the case of motor speed change |
通过比较图 11、图 12和图 13可以看出,当在给定转速在0.2 s突变时,采用PI速度调节器的系统,其转速响应产生超调,转矩响应有一个正脉冲; 而采用SM和ADRC速度调节器的系统,其转速响应平稳无超调.因此,基于ADRC和基于SM的系统比基于PI的系统有更强的跟踪给定转速变化的能力.
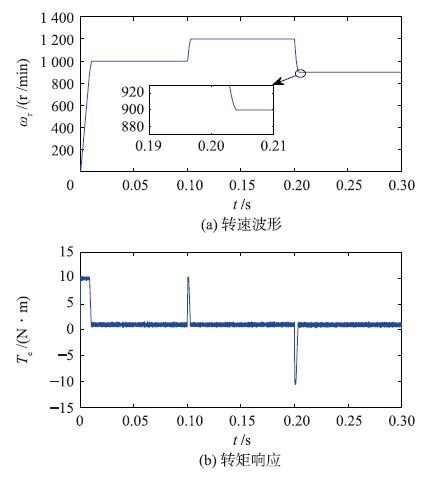
|
| 图 13 转速变化时采用ADRC速度调节器的系统动态响应 Figure 13 The system dynamic responses of based-ADRC speed regulator in the case of motor speed change |
本文对MC驱动PMSM系统进行了数学建模分析,提出了基于ADRC的DTC策略.设计了ADRC速度调节器,将MC驱动的DTC系统分为3部分: 虚拟交—直变换器、虚拟直—交变换器以及MC开关选择,并给出了其清晰设计思路和方法.所设计的系统具有较好的转速和转矩控制效果、且输入侧PF能够达到1.与基于PI的DTC系统相比,本文基于ADRC速度调节器的DTC系统具有更强的抗负载扰动和跟踪给定转速变化的能力,能够克服响应速度和稳定精度之间的矛盾; 与基于SM的DTC系统相比,基于ADRC的DTC系统具有更好的抗负载扰动能力,能够避免SM控制系统固有抖振的缺点.仿真结果验证了所提方法的可行性和正确性.
附录SM速度调节器设计
当忽略库仑摩擦转矩和粘滞摩擦系数,PMSM机械转动方程为
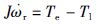
|
定义滑模面为S=ωr-ωr*,对S求导得
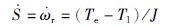
|
(19) |
为保证系统具有良好的动态响应,选取指数趋近律来设计SM速度调节器,即
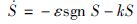
|
(20) |
式中: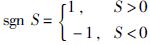
结合式(18)和式(19)可得SM速度调节器输出为
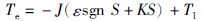
|
(21) |
上述所设计的SM速度调节器稳定性证明如下:
选取李亚普诺夫函数V=S2/2,其导数为

|
(22) |
将式(20)代入式(22)得
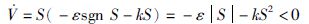
|
根据李亚普诺夫稳定性理论,SM速度调节器(21)是渐近稳定的.
| [1] | 张绍, 周波, 仇红奎. 永磁同步电机-矩阵变换器新型电流调制策略研究[J]. 中国电机工程学报, 2008, 28 (21): 90–95. Zhang S, Zhou B, Chou H B. Novel current modulation strategy of permanent magnet synchronous machine and matrix converter[J]. Proceedings of the CSEE, 2008, 28 (21): 90–95. |
| [2] | Casadei D, Serra G, Tani A, et al. Optimal use of zero vectors for minimizing the output current distortion in matrix converters[J]. IEEE Transactions on Industrial Electronics, 2009, 56 (2): 326–336. DOI:10.1109/TIE.2008.2007557 |
| [3] | Sun Y, Su M, Li X, et al. A general constructive approach to matrix converter stabilization[J]. IEEE Transactions on Power Electronics, 2013, 28 (1): 418–431. DOI:10.1109/TPEL.2012.2199767 |
| [4] | Khwan-on S, de Lillo L, Empringham L, et al. Fault-tolerant matrix converter motor drives with fault detection of open switch faults[J]. IEEE Transactions on Industrial Electronics, 2012, 59 (1): 257–268. DOI:10.1109/TIE.2011.2162711 |
| [5] | 周波, 秦显慧, 雷家兴, 等. 矩阵变换器应用于电机系统的研究与进展[J]. 南京航空航天大学学报, 2014, 46 (1): 1–10. Zhou B, Qin X H, Lei J X, et al. Review of matrix-converter application in electric machine systems[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46 (1): 1–10. |
| [6] | 汪海波, 周波, 方斯琛. 永磁同步电机调速系统的滑模控制[J]. 电工技术学报, 2009, 24 (9): 71–77. Wang H B, Zhou B, Fang S C. A PMSM sliding mode control system based on exponential reaching law[J]. Transactions of China Electrotechnical Society, 2009, 24 (9): 71–77. |
| [7] | 李宁, 李亚光, 王宏兴, 等. 分数阶永磁同步电机混沌系统模糊跟踪控制[J]. 信息与控制, 2016, 45 (1): 8–13. Li N, Li Y G, Wang H X, et al. Fuzzy tracking control for fractional-order permanent magnet synchronous motor chaotic system[J]. Information and Control, 2016, 45 (1): 8–13. |
| [8] | Zhang B T, Pi Y G. Robust fractional order proportion-plus-differential controller based on fuzzy inference for permanent magnet synchronous motor[J]. IET Control Theory & Applications, 2012, 6 (6): 829–837. |
| [9] | 韩京清. 自抗扰控制技术[J]. 前沿科学, 2007 (1): 24–31. Han J Q. Auto disturbances rejection control technique[J]. Frontier Science, 2007 (1): 24–31. |
| [10] | 韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998, 13 (1): 19–23. Han J Q. Active disturbance rejection controller and its application[J]. Control and Decision, 1998, 13 (1): 19–23. |
| [11] | Han J Q. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56 (3): 900–906. DOI:10.1109/TIE.2008.2011621 |
| [12] | Sun D. Comments on active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2007, 6 (54): 3428–3429. |
| [13] | Sira-Ramírez H, Linares-Flores J, García-Rodríguez C, et al. On the control of the permanent magnet synchronous motor:An active disturbance rejection control approach[J]. IEEE Transactions on Control Systems Technology, 2014, 22 (5): 2056–2063. DOI:10.1109/TCST.2014.2298238 |
| [14] | Li S H, Xia C J, Zhou X. Disturbance rejection control for method permanent magnet synchronous motor speed-regulation system[J]. Mechatronics, 2012, 22 (6): 706–714. DOI:10.1016/j.mechatronics.2012.02.007 |
| [15] | 韩京清, 张荣. 二阶扩张状态观测器的误差分析[J]. 系统科学与数学, 1999, 19 (4): 465–471. Han J Q, Zhang R. Error analysis of the second order ESO[J]. System Science and Mathematical Sciences, 1999, 19 (4): 465–471. |
| [16] | 张绍, 周波, 葛红娟. 基于双空间矢量调制的矩阵变换器-永磁同步电机矢量控制系统[J]. 电工技术学报, 2007, 22 (4): 47–52. Zhang S, Zhou B, Ge H J. Vector control system of permanent magnet synchronous motor based on double space vector modulated matrix converter[J]. Transactions of China Electrotechnical Society, 2007, 22 (4): 47–52. |
| [17] | 王晶鑫, 姜建国. 基于磁场定向的矩阵变换器驱动感应电机变结构直接转矩控制[J]. 中国电机工程学报, 2010, 30 (6): 57–62. Wang J X, Jiang J G. Variable-structure direct torque control for induction motor driven by a matrix converter based on field oriented[J]. Proceedings of the CSEE, 2010, 30 (6): 57–62. |
| [18] | Xia C L, Zhao J X, Yan Y, et al. A novel direct torque control of matrix converter-fed PMSM drives using duty cycle control for torque ripple reduction[J]. IEEE Transactions on Industrial Electronics, 2014, 61 (6): 2700–2713. DOI:10.1109/TIE.2013.2276039 |
| [19] | 孙凯, 黄立培, 梅杨. 矩阵式变换器驱动异步电机调速系统的非线性自抗扰控制[J]. 电工技术学报, 2007, 22 (12): 39–45. Sun K, Huang L P, Mei Y. A nonlinear auto-disturbance rejection control for matrix converter fed induction motor drive system[J]. Transactions of China Electrotechnical Society, 2007, 22 (12): 39–45. |
| [20] | 韩京清. 自抗扰控制技术:估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社 ,2008 : 192 -206. Han J Q. Active disturbance rejection control technique:The technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press , 2008 : 192 -206. |
| [21] | Sabanovic A. Variable structure systems with sliding modes in motion control-a survey[J]. IEEE Transactions on Industrial Informatics, 2011, 2 (7): 212–223. |
| [22] | Su Y X, Zheng C H, Duan B Y. Automatic disturbances rejection controller for precise motion control of permanent-magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2005, 52 (3): 814–823. DOI:10.1109/TIE.2005.847583 |
| [23] | 刘清. 基于自抗扰控制器的永磁同步电机伺服系统控制策略的研究及实现[D]. 天津:天津大学, 2011. Liu Q. Research and realization of the control strategy for PMSM servo system based on auto-disturbances rejection controller[D]. Tianjin:Tianjin University, 2011. |
| [24] | 王庆龙, 张兴, 张崇巍. 永磁同步电机矢量控制双滑模模型参考自适应系统转速辨识[J]. 中国电机工程学报, 2014, 34 (6): 897–902. Wang Q L, Zhang X, Zhang C W. Double sliding-mode model reference adaptive system speed identification for vector control of permanent magnet synchronous motors[J]. Proceedings of CSEE, 2014, 34 (6): 897–902. |



