1 引言
随着科学技术的高速发展,大多数化工过程生产规模越来越大,系统越来越复杂,可以将其视为一种大系统.大系统维数较高,通常含有多个输入输出,结构复杂,传统控制方法难以取得很好的效果; 通常将大系统按照工业流程单元分解为多个子系统,各个子系统间相互影响,耦合程度较高.
流程工业大系统的控制主要有2种结构: 一种为集中式控制,一种为分布式控制.其中,在集中式结构中,多个子系统由一个控制器集中控制; 在分布式结构中,各个子系统分别由一个控制器单独控制,同时各个控制器间会互相传递其各个子系统的过程信息.由于集中式模型预测控制需要处理大量的输入输出信息,导致单个集中式预测控制器负担过重,因此通常采用分布式模型预测控制算法,每个子系统分别采用一个预测控制器来进行控制,多个预测控制器相互通信协助来共同解决整个大系统的优化问题[1].
面对流程工业大系统的优化问题,Li和Huang提出了一个流程雁阵(PGQ)方法[2-3],将工业生产流程按雁阵飞行机制进行分解,将整体目标的寻优结果转化为子雁阵的优化目标,依据子雁阵之间的信息传递关系建立多级流程雁阵模型,进行协调优化.在此基础上,Li和Huang针对当监控变量发生变化时经济性能指标会偏离最优轨迹的情况,结合流程雁阵方法,提出了基于监控的实时优化算法,同时将该算法应用于TE(Tennessee Eastman)过程,并与常规的整体优化策略进行对比,结果表明该文中提出的算法计算负担大大减小[4].另外,为了将流程雁阵方法与过程建模和优化相结合,Li和Huang又提出了一种基于传感器的流程雁阵,将与过程单元有关的传感器组成雁阵结构[5].因此可以将工业过程模型分解为多个递阶相连的传感器阵列(SGQs),每个传感器雁阵都有其独立的优化目标.该方法高效利用了过程传感器测量值,将该算法应用于实际工程证明其有效性.由于常规的实时优化算法通常具有过程模型规模太大,过程操控变量太多等缺陷,Li和Huang引入流程雁阵方法来对实时优化算法进行改进,将过程实时优化和各级子雁阵中子雁头雁位置的跟踪传递相联系,给出了相应的阵形自主调整规则和实施方法[6].针对阵形自主调整的缺陷,张娜等[7]提出一种两级同时调整的状态空间模型预测控制方法.然而,该方法需迭代至各个子雁阵均达到稳定状态才能达到收敛,调整时间过长.
在模型预测控制基础上,Zheng等[8-9]提出了一个新颖的分布式模型预测控制方法.常规的分布式模型预测控制中,各个子系统的控制器需要互相传递信息,而该算法利用子系统间的网络结构,使传递信息量大大减少.同时,各个子系统的优化指标也进行了相应的调整,不只优化本子系统的目标函数,还将其邻域内相关子系统的目标函数考虑在内.最后通过连续加热过程对算法的有效性进行了验证.Ruben等[10]针对大系统中子过程间共享生产资料这一问题,提出了一种带有协调器的分布式模型预测控制方法,保证了整体约束条件的实现.Stewart等[11]提出一种基于协作的分布式模型预测控制算法,该算法可以适用于任何含有有限个子系统的大系统,并且满足系统稳定性条件.文[12]研究了顺序递阶求解的分布式模型预测控制的算法结构及控制器设计方法.针对串联生产过程的特殊结构,蔡星等[13]和陈庆等[14]分别提出了适用于这种结构的分布式模型预测控制算法,其中蔡星等将递阶求解应用到串联结构中,而陈庆提出了一种基于前馈补偿的解耦控制算法.文[15]将传统分布式模型预测控制方法和基于串联结构的顺序递阶求解的分布式模型预测控制进行了对比,并通过工程实例应用证明了后者的优越性.然而,传统的分布式预测控制算法,多要经历一个漫长的迭代过程才能保证各个子系统均达到收敛,针对多级流程雁阵这种典型的串联结构,利用其本身的拓扑结构,利用上下级子雁阵间的信息传递,可以有效地简化算法.
子空间辨识算法作为线性状态空间模型的辨识方法,是模型辨识领域最活跃的研究方向之一,是一种真正意义上的多输入多输出辨识法,在工业应用中具有重要的实际意义[16].通常利用过程输入输出数据的Hankel矩阵辨识得到状态空间模型,进而进行状态空间模型预测控制.然而,这一过程计算量很大且预测控制是一种基于模型的控制算法,根据预测模型来估计系统行为并进行优化问题的求解,因此模型精度对控制器的性能有较大的影响.基于上述原因,Cui等[17]提出一个基于子空间辨识的模型预测控制方法,直接利用子空间辨识方法获取对象脉冲响应序列矩阵,并将其用于预测控制,取得了很好的控制效果.
本文提出了一种基于子空间辨识的分布式模型预测控制算法,并将其应用于多级流程雁阵的阵形调整,利用流程雁阵的特殊结构简化了分布式模型预测控制算法,并解决了预测控制对模型精度的依赖性较大的问题,减轻了计算负担.
2 多级流程雁阵的分布式状态空间模型预测控制算法 2.1 多级流程雁阵的状态空间模型流程雁阵思想来自自然界中雁阵飞行机理,用于解决流程工业系统的分解协调优化问题.
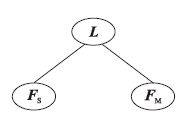
定义1(流程雁阵) 一个基本的流程雁阵模型如图 1所示,其中L为头雁位置,FS为状态子雁位置,FM为操纵子雁位置.
|
| 图 1 流程雁阵结构图 Figure 1 Structure of a PGQ |
此流程雁阵的优化问题描述下:
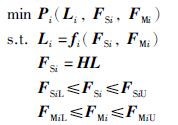
|
(1) |
其中,Pi为PGQi的性能指标,fi表示PGQi的头雁位置和其状态子雁位置、操纵子雁位置间的关系,FSiL和FMiL分别表示PGQi的状态子雁位置和操纵子雁位置的下限值,FSU和FMiU分别表示PGQi的状态子雁位置和操纵子雁位置的上限值,H为单位矩阵,代表流程雁阵之间的相连信息.
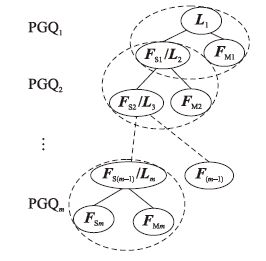
定义2(多级流程雁阵) 多级流程雁阵是依据工业过程的具体流程结构建立的递阶形式的系统,下一级流程雁阵通过头雁位置等价于上一级的状态子雁位置来实现两级之间的联接,如图 2所示.
|
| 图 2 多级流程雁阵结构 Figure 2 Structure of multi-level PGQs |
定义3(流程雁阵目标) 流程雁阵目标对应于实际流程工业的经济优化目标,即:
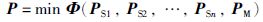
|
(2) |
其中,PSj(j=1,2…,n)和PM分别表示状态变量和操纵变量,j为状态变量个数.
流程雁阵的最优阵形调整即为系统从第1级开始依次进行跟踪、交换及传递.FSi与Li+1存在关系FSi=Li+1,即FSi与下一级的头雁位置Li+1相同.
每一级子雁阵的状态空间模型为
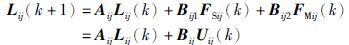
|
(3) |
其中,Aij、Bij均为状态空间模型的参数矩阵,i表示第i级子雁阵,j表示该子雁阵位于多级流程雁阵的第j个分支,并且有:
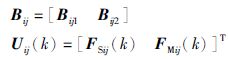
|
因此,其阵形调整可以表示成如下的数学问题:
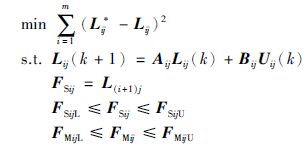
|
(4) |
这里,采用子空间辨识算法建立流程雁阵的状态空间模型,其基本步骤包括: 计算特定Hankel矩阵的行空间投影; 通过奇异值分解,直接计算获得广义能观矩阵或状态序列的卡尔曼滤波估计; 利用广义能观矩阵或状态序列的卡尔曼滤波估计确定系统参数矩阵.
为书写方便,本文仅对多级流程雁阵的第1个分支中的子雁阵做相关研究,以下均用PGQi代替PGQij,因此对于如下式表示的PGQi:
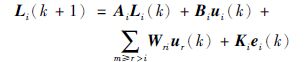
|
(5) |
其中,ur(k)为之前各级子雁阵的输入,Wui为耦合系数,ei(k)为误差项,Ki为其参数矩阵.令k=N,有:
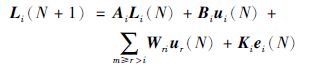
|
(6) |
再令k=N+1,有:
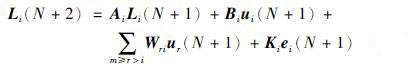
|
(7) |
将式(6)代入式(7)得
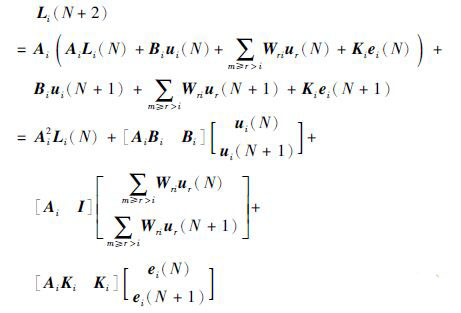
|
(8) |
以此类推可以得到:

|
(9) |
综合上式可以得到:

|
(10) |
因此,可以得到:
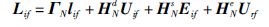
|
(11) |
其中,

|

|
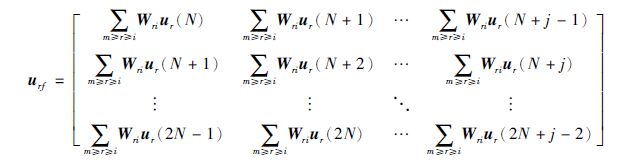
|
通过奇异值分解可得到广义能观矩阵ΓN,进而可以计算得到参数矩阵Ai,通过求解可得HNd.
模型算法控制(MAC)采用系统脉冲响应序列这一非参数模型作为系统的内部模型,利用过去和未来的输入输出信息,根据内部模型预测未来的输出状态,经模型输出误差进行反馈校正后,再与参考输入轨迹比较,应用二次型性能指标进行滚动优化,然后计算当前时刻应加于系统的控制动作,完成整个控制循环.因此可以省去后续状态空间模型参数的计算过程,利用HNd直接进行模型算法控制(MAC).
并且由于PGQi之前的子雁阵的子雁位置为已知,则Consti为已知.
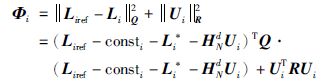
|
(13) |
其中,
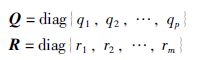
|
得到控制率:
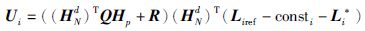
|
(14) |
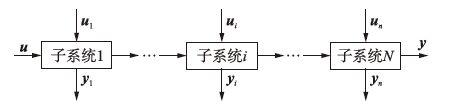
图 3所示为一个串联生产过程,它有N个子过程,每个子过程有独立的输入和输出,整个过程的控制目标为保证每个子过程的输出维持在其设定值附近.
|
| 图 3 串级结构 Figure 3 Serially connected structure |
可以发现,串联结构中子系统的输出仅受其上游子系统的影响,因此可以利用这种拓扑结构来减少子系统间的通信,Cai[13]等提出了一种可以反映系统输入耦合的复合模型,其中,xiT=[xi1T xi2T … xiiT … xiMT]T表示第i个子系统的状态,每个子系统状态被分为M个分量,xij表示第j个子系统的输入对第i个子系统的输出的影响而得到的状态,并且只受uj的影响,Wij为第i个子系统与第j个子系统相应的耦合系数.
因此第i个子系统的状态方程为
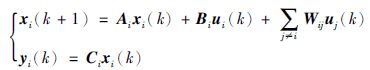
|
(15) |
由于每个子系统的输出仅与其上游子系统的控制作用有关,在此认为每个子系统仅优化其本身和其上游子系统的目标函数,该目标函数为
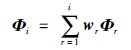
|
(16) |
其中,Φi为第i个子系统的目标函数.并且认为每个子系统的上游控制输入为已知,即只有该子系统的控制输入会影响该子系统,而不是该子系统和上游子系统的输入综合控制,因此只需要上游至下游的信号传递,也不存在迭代,以各个子系统顺序递阶的通信方式代替各个子系统同步迭代更新的通信方式,极大地减少了算法的通信负担.
因此第i个子系统的优化目标及约束条件可以表示为
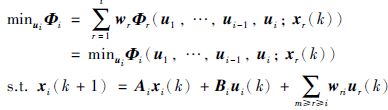
|
(17) |
其中,u1,…,ui-1为前i-1个子系统已知的控制输入,作为已知量给第i个子系统.
多级流程雁阵是一种典型的串级结构,根据以上思路,子雁阵PGQi的状态空间模型可以改进为
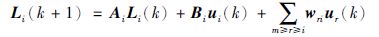
|
(18) |
对于图 2所示的多级流程雁阵结构,PGQi的头雁位置受本级子雁阵和它之前几级子雁阵的子雁位置综合影响,导致目标优化问题的求解极为复杂,因此在此采用基于串联结构的分布式模型预测控制算法,认为PGQi之前的子雁阵的子雁位置为已知,各个子雁阵优化问题顺序递阶求解,简化了优化问题求解,减少了通信负担.
因此,PGQi的优化目标可以改进为
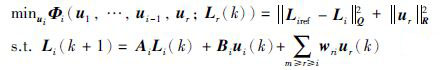
|
(19) |
对图 2所示的多级雁阵,最终的性能指标只和最高一级子雁阵得目标函数有关,当k时刻受到干扰影响,L2(k)偏离最优值,根据输出设定值,从最低一级雁阵顺序递阶求出子雁位置,直到求出PGQ1操纵子雁位置FM1(k),假定此时PGQ3之前的子雁阵经过和PGQ2相同的算法过程得到了子雁位置并且传递到PGQ2,那么以PGQ2为例,其模型预测算法如下:
(1) PGQ2的预测矩阵
PGQ2的状态空间模型为
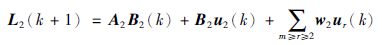
|
(20) |
通过子空间辨识得到脉冲相应序列Hp和参数矩阵A2.对式(20)进行迭代可以得到:

|
(21) |
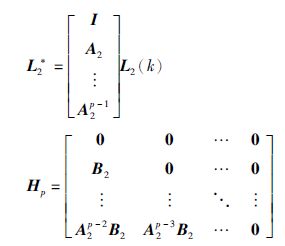
令:
|
(2) PGQ2优化问题的求解
PGQ2的目标函数为
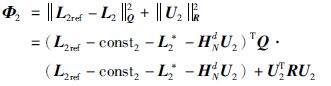
|
(22) |
通过求解得到子雁位置:
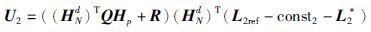
|
(23) |
可以得到PGQ2的操纵子雁位置.
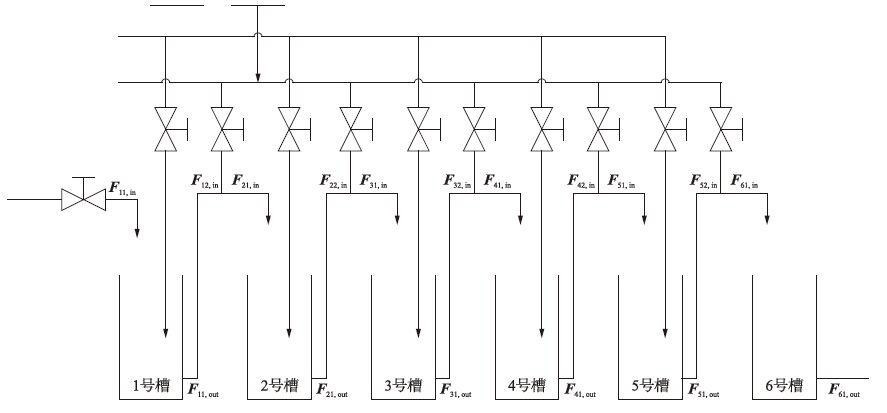
4 实例研究图 4所示为一个生产氢氧化铝的氧化铝碳酸化分解过程,将二氧化碳气体通入铝酸钠和氢氧化钠的混合溶液中,生成氢氧化铝,反应方程式如下:
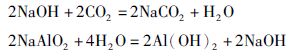
|
|
| 图 4 氧化铝碳酸化分解 Figure 4 Alumina carbonate decomposition |
在生产的工业流程中,连续碳酸化分解通过6个连续分解槽相互联接.脱硅后的NaAlO2物料首先进入高位槽,在该分解槽中通入气体进行如上化学反应,从1号槽底部流出的NaAlO2和NaOH溶液等物料,通过低压提料进入2号分解槽,按上述方法依次将料送入下一分解槽,用于提料的低压风流量也起到维持分解槽液位稳定的作用.前5台槽按分解率要求通入相应量的物料进行分解.6号槽是出料槽,合格产物通过出料泵进入沉降槽,其底流送往过滤机进行过滤,得到氢氧化铝产品.
在此,可以将把每一个分解槽看作一个子雁阵,第i号槽的NaAlO2和NaOH溶液流量为状态子雁位置向量,记为Fi1,in,CO2气体流量为操纵子雁位置向量,记为Fi2,in,而流出的NaAlO2、NaOH和Al(OH)3流量为头雁位置向量,记为Fi1,out,由于第i槽的头雁位置向量是第i+1槽的状态子雁位置向量,因此有Fi1,out=F(i+1)1,in.
在多级流程雁阵中,最终目标函数由最高一级子雁阵的头雁位置决定,分解过程的优化目标是氢氧化铝产量最大,由于6号槽为出料槽,不参与反应过程,故优化目标函数由6号槽的状态子雁位置决定,即P=max(xi2,F61,in),其中xi2为输出溶液中Al(OH)3的浓度.
给出氧化铝碳分解过程动态模型的传递函数矩阵描述如下式所示.其中Li为第i个槽NaAlO2出口流量,FMi为第i个槽的CO2流量,i=1,2,…,5.
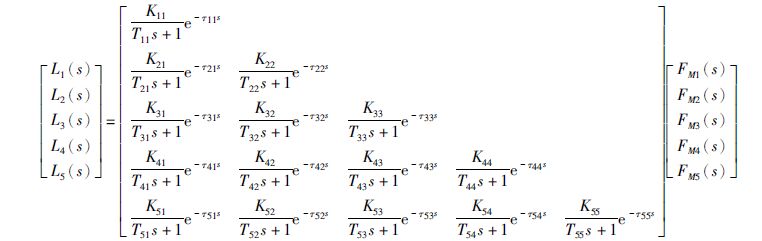
|
控制输入满足以下约束:
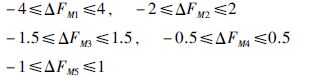
|
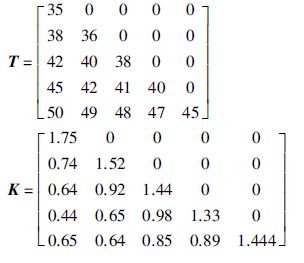
其中,参数矩阵如下所示,T和τ单位为min:
|

|
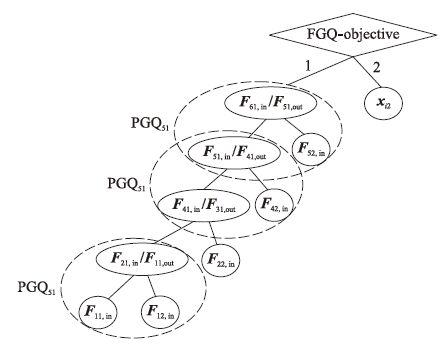
综上所述,可以建立此系统的流程雁阵结构,如图 5所示.
|
| 图 5 氧化铝碳酸化分解过程的多级流程雁阵结构 Figure 5 Multi-level PGQs of alumina carbonate decomposition |
根据流程雁阵的静态优化算法,确定PGQ51,PGQ41,…,PGQ11的头雁位置分别为23、61、85、90、94.
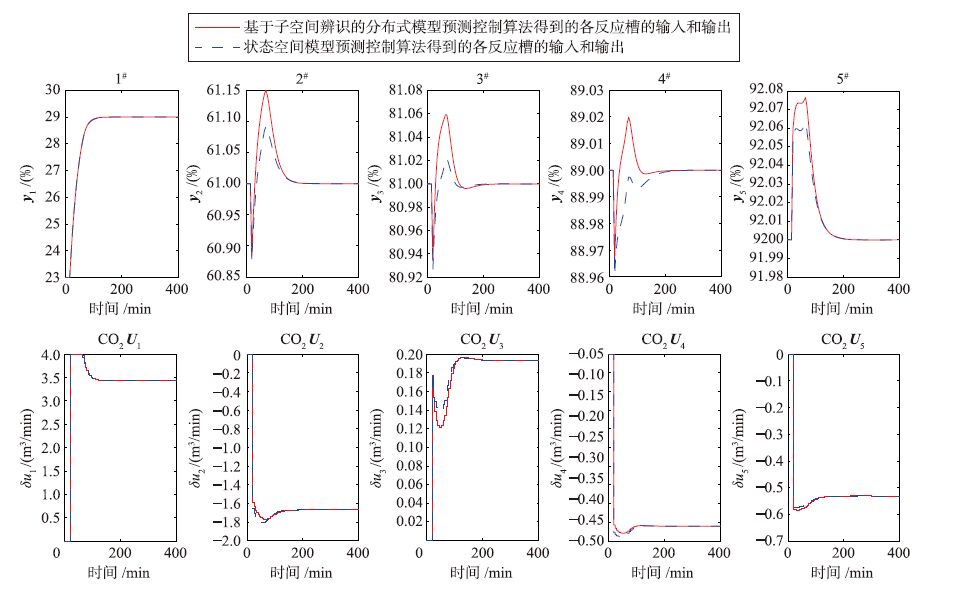
假设在运行过程中,当t=20 min时PGQ51受到干扰,头雁位置改变为29,这相当于给PGQ51一个阶跃扰动.按照多级流程雁阵的分布式模型预测控制算法,系统从PGQ51开始逐级进行调整,本级调整到稳定状态后即把最优控制输入传递到上一级子雁阵,进行顺序递阶求解,各流程雁阵的头雁和操纵子雁的变化即各反应槽的输出和输入如图 6所示,其中实线为基于子空间辨识的分布式模型预测控制算法,虚线为状态空间模型预测控制算法[11].可以发现,两种算法都可以使系统达到稳定,因此基于子空间辨识的分布式模型预测控制算法也可以实现有效控制.然而,由于基于子空间辨识的分布式模型预测控制算法避免了迭代过程,相比于状态空间模型预测控制算法迭代次数要小,计算量也大大减少.
|
| 图 6 基于子空间辨识的分布式模型预测控制与状态空间模型预测控制 Figure 6 Distributed model predictive control and state-space model predictive control |
针对多级流程雁阵这种特殊结构,本文提出一种基于子空间辨识的分布式模型预测控制算法,对于串联的多个子雁阵,顺序递阶地求解各个子雁阵的优化问题,并且在求解某一级子雁阵的优化问题时,认为其以上各级子雁阵的最佳子雁位置为已知,避免了迭代过程,同时通过子空间辨识方法直接获取对象脉冲响应序列矩阵,并将其用于预测控制,省去了参数辨识这一步,极大得减少系统的计算负担.最后,将这一方法应用于氧化铝碳酸化分解过程,仿真结果证明该算法具有较好的控制效果.
本文只针对多级流程雁阵的单个分支进行了研究,而多个分支之间会存在一定的相互影响,这种耦合作用的存在可能会降低算法的性能,因此今后将进一步研究多分支多级流程雁阵的阵形调整问题.
| [1] | 张绍, 周波, 仇红奎. 永磁同步电机-矩阵变换器新型电流调制策略研究[J]. 中国电机工程学报, 2008, 28(21):90-95. |
| [2] | Li H, Huang J. Process goose queue (PGQ) approaches toward plantwideprocess optimization with applications in supervision-driven real-time optimization[J]. Industrial & Engineering Chemistry Research, 2012, 51 (33): 255–263. |
| [3] | Huang J, Hongguang L I. A novel real-time optimization methodology for chemical plants[J]. Chinese Journal of Chemical Engineering, 2012, 20 (6): 1059–1066. DOI:10.1016/S1004-9541(12)60587-4 |
| [4] | Huang J, Li H. Sensor-goose queue (SGQ) approaches with applications in process modeling and optimization[J]. Sensor Letters, 2013, 11 (5): 836–844. DOI:10.1166/sl.2013.2675 |
| [5] | Huang J W, Li H G. Process goose queue methodologies with applications in plant-wide process optimization[J]. Journal of Computers, 2012, 7 (10): 2462–2470. |
| [6] | Huang J W, Li H G. Plant-wide process real-time optimization based on process goose queue methodology[J]. Procedia Engineering, 29, 2012 : 2526–2531. |
| [7] | 张娜, 李宏光, 黄静雯. 流程雁阵阵形调整的状态空间模型预测控制方法[J]. 上海交通大学学报, 2016, 50 (6): 943–948. Zhang N, Li H G, Huang J W. A state space model predictive control approach to fromation adjustments of process goose queues[J]. Journal of Shanhai Jiao Tong University, 2016, 50 (6): 943–948. |
| [8] | Zheng Y, Li S, Li N. Distributed model predictive control over network information exchange for large-scale systems[J]. Control Engineering Practice, 2011, 19 (7): 757–769. DOI:10.1016/j.conengprac.2011.04.003 |
| [9] | Zheng Y, Li S, Qiu H. Networked coordination-cased distributed model predictive control for large-scale system[J]. IEEE Transactions on Control Systems Technology, 2013, 21 (3): 991–998. DOI:10.1109/TCST.2012.2196280 |
| [10] | Martí R, Sarabia D, Navia D, et al. A method to coordinate decentralized NMPC controllers in oxygen distribution networks[J]. Computers & Chemical Engineering, 2013, 59 (10): 122–137. |
| [11] | Stewart B T, Venkat A N, Rawlings J B, et al. Cooperative distributed model predictive control[J]. Systems & Control Letters, 2010, 59 (8): 460–469. |
| [12] | Scattolini R. Architecture of distributed and hierarchical model predictive control-A review[J]. Journal of Process Control, 2009, 19 (5): 723–731. DOI:10.1016/j.jprocont.2009.02.003 |
| [13] | 蔡星, 谢磊, 苏宏业, 等. 基于串联结构的分布式模型预测控制[J]. 自动化学报, 2013, 39 (5): 510–518. Cai X, Xie L, Su H Y, et al. Distributed model predictive control based on cascade processes[J]. Automatica, 2013, 39 (5): 510–518. |
| [14] | 陈庆, 李少远, 席裕庚. 一类串联生产过程的分布式解耦预测控制[J]. 控制与决策, 2004, 19 (6): 647–650. Chen Q, Li S Y, Xi Y G. Distributed decoupling predictive control of a kind of cascade processes[J]. Control and Decision, 2004, 19 (6): 647–650. |
| [15] | Wang D, Glavic M, Wehenkel L. Comparison of centralized, distributed and hierarchical model predictive control schemes for electromechanical oscillations damping in large-scale power systems[J]. International Journal of Electrical Power & Energy Systems, 2014, 58 (6): 32–41. |
| [16] | Favoreel W, Moor B D, Overschee P V. Subspace state space system identification for industrial processes[J]. Journal of Process Control, 2000, 10 (2/3): 149–155. |
| [17] | Huang B, Kadali R. Dynamic modeling, predictive control and performance monitoring:A data-driven subspace approach[M]. Berlin, Germany: Springer-Verlag , 2008 . |



