2. 中国科学院大学, 北京 100049;
3. 密歇根州立大学, 美国 密歇根州东兰辛
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Michigan State University, East Lansing MI, USA
1 引言
Hadamard矩阵(在基二快速Hadamard变换的语境下这里具体指Hadamard定序的Walsh-Hadamard矩阵或称Sylvester矩阵,下文简称为H阵)是一种结构特殊的矩阵,可以通过如下方法迭代构造:
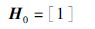
|
(1) |
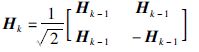
|
(2) |
其中,k是一个正整数[1].H阵除去归一化因子外只包含1和-1两种元素,不同两行之间可以构成相互正交的行向量,而且它和一个列向量的乘积可以用快速Hadamard变换进行计算,其时间复杂度仅为O(nlnn)[1].因为这些优越的性质,H阵被广泛应用于数字信号和图像处理(信号表达、滤波、编码、数据压缩)[1-2],生物医学信号分析[3]、通信系统[2, 4]、数字逻辑[5]、量子计算[6]等领域中.
单像素相机是Takhar等[7]在2006年提出的一种新型成像设备,为非可见光光谱感光元件目前难以制造为阵列成像的问题提供了一种解决方案,H阵在其中的应用可以显著地加速曝光过程[8]及图像重构[9].单像素相机包含3个主要部件[7, 10-14]: 单像素传感器、光调制元件(如数字微镜器件(digital micro-mirror device,DMD),下文以DMD为例说明)和透镜组.在压缩感知的框架中它的测量过程可以建模为y=Ax,其中x为长度n的实数列向量,表示一个$\sqrt{n}\times \sqrt{n}$像素的离散图像; A为m行n列的预先设计好的实数测量矩阵,m<n,其中每一行元素的正负表达了一次测量当中DMD每一个微镜角度的“开关”状态; y为长度m的实数列向量,表达一共m次的测量结果.在测量完成之后,y和A均为已知,利用图像梯度的稀疏性,原图像x一般通过y=Ax或||Ax-y||2<ε约束下最优化问题minxTV(x)来求解[9, 15],其中TV(x)表示x的总变差范数.解该最优化问题的一种高效算法是增广拉格朗日乘子和交替方向乘子法,而这个算法需要频繁计算矩阵A与向量的乘积[9].以30%的测量数和1 024×1 024像素的图像为例,对应的矩阵A有314 573行和1 048 576列,类似这样大型的矩阵和向量的乘法需要消耗较多的计算时间.为了加速这个乘法运算,通常采用打乱排列的H阵作为测量矩阵A=P1HkP2,其中P1为取n×n排列矩阵最上面m行得到的m×n矩阵,P2为另一个n×n排列矩阵.这样的构造一方面满足了压缩感知实践上对于测量矩阵的随机性要求,另一方面因为对向量x而言Ax=P1(Hk(P2x))仅仅需要进行2次时间复杂度为O(n)的向量排列操作以及1次时间复杂度为O(nlnn)的快速Hadamard变换,这就把矩阵向量相乘一般情况下的时间复杂度O(n2)改进到了O(nlnn)[1].
单像素相机图像分辨率的不断提高使得测量矩阵的维数也随之增加.这个过程中,快速Hadamard变换的执行时间以线性对数(linearithmic)的方式进行增长[16],即当图像x的长度增加为原来的c倍时,计算时间大约会变为原来的(1+lnc/lnn)c倍.随着n不断增大,快速Hadamard变换的计算将面临新的挑战.因此,为了解决规模比较大的快速Hadamard变换计算速度的问题,本文提出一种基二快速Hadamard变换的任务级并行算法.
2 算法设计 2.1 经典串行基二快速Hadamard变换与快速傅里叶变换类似,基二快速Hadamard变换可以通过蝴蝶运算结构来实现.因为这些结构在计算时间复杂度上的等价性,不失一般性地,本文选用序列定序的Walsh-Hadamard矩阵(下文简称为W阵)来设计并行算法.H阵和W阵之间存在双射关系:
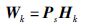
|
(3) |
其中,Ps为排列矩阵[17],脚标s代表对应的排列函数s(p)=r(g(b(p))),p=0,1,…,2k-1: b(p)计算p的二进制形式,g()计算一个二进制整数对应的格雷码,r()将输入的二进制位按照k位的宽度逆序,并返回对应的整数值[1].换言之,矩阵Wk的第p行与矩阵Hk的第s(p)行是一样的.以k=3,即8阶W阵为例:
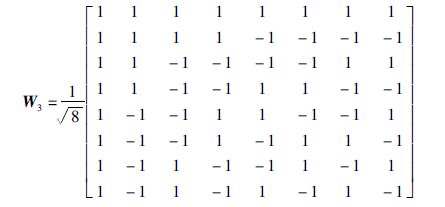
|
计算X=Wx的串行基二快速Hadamard变换算法的具体实现过程如下[9]:
Step 1 输入长度为n=2k的向量x=[x0,x1,…,xn-1]T.算法初始化申请长度为n的临时向量t=[t0,t1,…,tn-1]T和q=[q0,q1,…,qn-1]T.
Step 2 阶段1(对t进行循环赋值初始化): i=0,2,…,n-2,步长为2,计算ti=xi+xi+1和ti+1=xi-xi+1.
Step 3 阶段2至k(蝶形运算): 初始化计数器cs=2,l=1,进入循环:
1) 若cs>k终止循环,跳到Step 4.
2) 赋值m=2l,j=0,h=0.
3) 若h≥n-1跳到6).
4) 循环进行蝶形赋值: r=j,j+2,…,j+m-2,步长为2,赋值qh=tr+tr+m,qh+1=tr-tr+m,qh+2=tr+1-tr+m+1,qh+3=tr+1+tr+m+1,h=h+4.
5) 赋值j=j+2m,跳到3).
6) 至此当前阶段cs已完成,交换向量t和q的值(这样每个阶段的结果都保存到了向量t中).计数器cs和l自增1,跳回1).
Step 4 输出向量2-k/2t.算法结束.
通过上述算法计算输入长度为8的向量的例子X=W3x如图 1所示.其中实线表示正,虚线表示负,计算从左向右进行,每一个阶段结束时节点累加两条入射线的值.由图可见,蝴蝶运算的时间复杂度为O(nlnn).
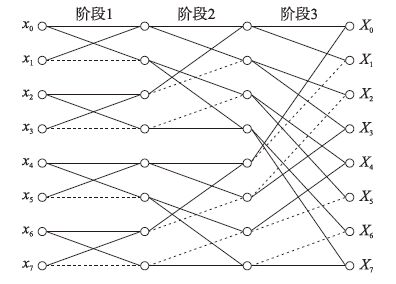
|
| 图 1 快速Hadamard变换蝴蝶运算示例X=W3x Figure 1 Example of butterfly diagram for fast Hadamard transform X=W3x |
快速Hadamard变换的反变换和正变换的形式完全一样.这是因为W阵是对称的酉矩阵[1],所以WTX=WTWx即有x=WTX=WX.
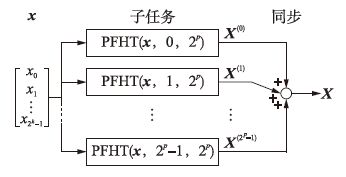
2.2 并行基二快速Hadamard变换要把总任务X=Wx进行任务级切分,直观的方法是将x分解为若干个向量的和x=∑ixi使得X=W∑ixi=∑iWxi,i=0,1,…,s-1,其中s表示子任务数.如果每个子任务X(i)=Wxi仅大约需要总任务时间的1/s,而且并行化带来的并行开销相对可以忽略不计,那么这样的任务分解是成功的.考虑长度为2k的向量x和xi,整数s=2p,p<k,将x等长度地划分为s段,选择其中的第i段作为xi的支撑,并令xi中其它元素为0,得到
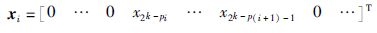
|
(4) |
根据串行基二快速Hadamard变换的算法,这样的分解对于分治处理的子任务有2个好处: 一是所需要的蝶形计算阶段数减少为k-p,二是在每一个蝶形运算阶段计算仅仅需要针对向量的支撑部分进行.
在串行算法的基础上,并行基二快速Hadamard变换子任务X(i)=Wxi的算法,即函数PFHT(x,i,s),具体实现过程设计如下:
Step 1 输入长度为n=2k的向量x=[x0,x1,…,xn-1]T,子任务数s=2p及子任务号i=0,1,…,s-1.算法初始化计算向量支撑部分的长度Ls=n/s,支撑起始位置下标ifrom=i×Ls,ito=ifrom+Ls-1,需要的阶段数S=k-p; 申请长度为n的临时向量t=[t0,t1,…,tn-1]T和q=[q0,q1,…,qn-1]T.
Step 2 阶段1(对t进行循环赋值初始化): a=ifrom,ifrom+2,…,ito-1,步长为2,计算ta=xa+xa+1和ta+1=xa-xa+1.
Step 3 阶段2至阶段S(蝶形运算): 初始化计数器cs=2,l=1,进入循环:
1) 若cs>S终止循环,跳到Step 4.
2) 赋值m=2l,j=ifrom,h=ifrom.
3) 若h>ito跳到6).
4) 循环进行蝶形赋值: r=j,j+2,…,j+m-2,步长为2,赋值qh=tr+tr+m,qh+1=tr-tr+m,qh+2=tr+1-tr+m+1,qh+3=tr+1+tr+m+1,h=h+4.
5) 赋值j=j+2m,跳到3).
6) 至此当前阶段cs已完成,交换向量t和q的值(这样每个阶段的结果都保存到了向量t中).计数器cs和l自增1,跳回1).
Step 4 扩散阶段(将向量t中下标ifrom至ito的结果“扩散”到整个向量作为结果).循环赋值: a=0,1,…,n-1,步长为1,计算sgn=parity(reverseBits(gray (a)) & ifrom),qa=sgn×tifrom+floor(a/s),其中gray()函数计算一个二进制整数对应的格雷码; reverseBits()函数将输入的二进制位按照k位的宽度逆序,并返回对应的整数值; 符号 & 表示整数按位与; parity()函数对整数的二进制位1进行计数,如果有奇数个1则返回-1,如果有偶数个1则返回1; floor()函数返回小于等于输入实数的最大整数.
Step 5 输出向量2-k/2q,即结果X(i).算法结束.
以输入长度向量为8的向量,子任务数为4,即k=3,p=2情况下子任务X(2)=Wx2的计算为例,如图 2所示.其中实线表示正,虚线表示负,计算从左向右进行.在本例中,蝴蝶运算只需要进行阶段1,在阶段1结束时,中间结果记为x′4和x′5.剩下的阶段则为一个扩散阶段,直接将x′4和x′5的值赋给X(2)的各个元素.
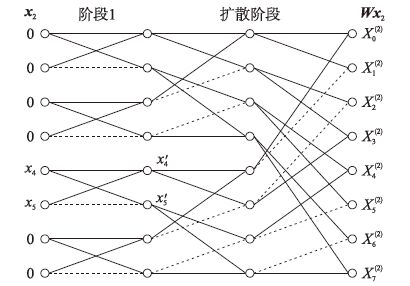
|
| 图 2 子任务X(2) = Wx2计算过程 Figure 2 Calculation process of subtask X(2) = Wx2 |
对比串行算法,并行子任务算法除了在计算的向量下标范围以及需要的阶段数不同之外,最后的p个阶段被替换为一个扩散阶段: 在完成蝴蝶运算阶段1至k-p后,对应于式(4)的中间结果
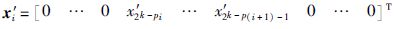
|
(5) |
将直接赋值给子任务的输出结果X(i),并调整其中每个元素的正负号,即
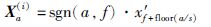
|
(6) |
其中a=0,1,…,n-1表示向量X(i)的下标,换言之X(i)=[X0(i),X1(i),…,Xn-1(i)]T; f=2k-pi是向量xi支撑起始的下标位置.为了使得通过式(6)计算的结果与X
根据定义式(4)及式(5),考虑并行子任务算法Step 3,可以得知在阶段1到阶段S蝶形运算的迭代过程中,中间结果x′f,x′f+1,…,x′f+2k-p-1中xf的符号并无改变,即:
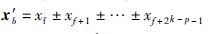
|
(7) |
其中b=f,f+1,…,f+2k-p-1,符号±表示算法针对不同的下标b迭代后的正号或负号结果.而最终结果向量X的第a个元素Xa可分解为Xa=∑i X(i)a,其中包含的xf成分的正负号恰好与W阵中的元素Wa,f一致.又因为H阵的元素可以通过公式:
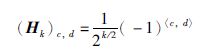
|
(8) |
直接计算得出,其中(Hk)c,d表示矩阵Hk的第c行第d列的元素(从0开始计数),c和d分别表示整数c和d对应的二进制位以向量表达的形式,〈c,d〉表示它们之间的内积[1].应用式(3),则式(6)中的符号调整函数可以构造如下:
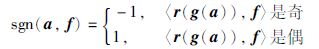
|
(9) |
其中a和f分别是整数a和f的二进制表达写为向量的形式,函数g(·)计算输入向量二进制形式的格雷码并以向量输出结果,函数r(·)对输入向量的元素进行逆序.这样的构造使得最终需要的结果可以通过所有子任务的结果累加得出,即:
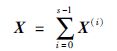
|
(10) |
其中s=2p为子任务数,如图 3所示.在上文并行算法的过程描述中,符号调整函数式(9)的实现采用了更利于编程实现的表达方式,将整数的位运算替代了向量运算.而对于常用的32位或64位整数,格雷码编码、按位逆序、位1奇偶计数都具有高效的位运算实现方式[18].此外,符合IEEE标准[19]定义的浮点数与-1的乘积可以简单地使用一次异或位运算实现.这样就避免了费时的循环和分支逻辑结构,使得算法的实现在多种计算平台上都能高效地执行.最终,整个并行开销主要取决于扩散阶段、同步及子任务向量累加的耗时.
|
| 图 3 完整并行算法框架示意图 Figure 3 Schematic diagram for parallelized framework |
尽管第2小节通过构造的方式说明了串行算法与并行算法数学上的等价性,因为浮点运算会引起精度损失,因而实际两种方法的计算结果会有轻微的差别.为了将这种差别量化,本文用串行的方式实现了式(10)作为仿真,亦即先使用并行算法中的子任务算法按顺序计算X(0),X(1),…,X(s-1),最后再累加起来.这样的好处是便于模拟子任务数非常多(s非常大)的情形,而误差与真正的并行计算保持一致.
设XS和XP分别表示串行算法与并行算法的计算结果.定义欧氏距离平方ε(k,p)=XS-XP2为并行算法的数值误差,分别针对不同的向量长度2k(k=10,11,…,20)及不同的子任务数2p(p=2,3,…,10)进行仿真,对于每一个情况:
1) 输入向量与输出向量的元素采用IEEE双精度浮点数表达;
2) 输入向量的每个元素采用均匀分布的[0,1]区间浮点伪随机数发生器产生;
3) 对于每一个k与p的组合,进行1 000次实验.将ε(k,p)视为随机变量,使用1 000个样本分别估计其均值和标准差.
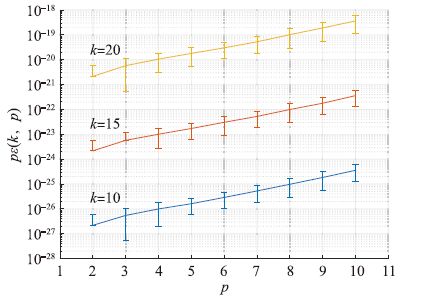
仿真结果如图 4所示(选取k=10,15,20),其中上下误差棒的长度表示标准差,当下界小于0时,下误差棒在对数坐标中不画出.仿真结果表明: 固定p,增大k,或者固定k,增大p,则误差ε(k,p)越大; 对于仿真中的最坏情况k=20和p=10,误差ε(k,p)小于10-18,因此在一般实践中可以忽略不计.
|
| 图 4 并行算法数值误差仿真 Figure 4 Numerical error of the parallel algorithm (simulation) |
在机理上,误差ε(k,p)是双精度浮点数在计算过程中的总体累积效果,与向量长度2k以及划分的子任务数2p有直接的关系,因此可以归纳出经验模型:

|
(11) |
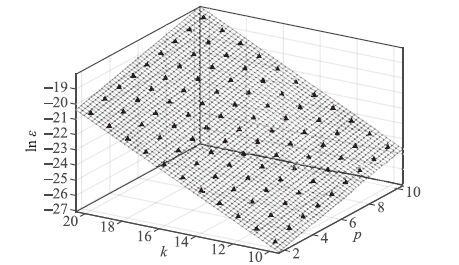
其中a,b,c都是常数.对所有k=10,11,…,20及p=2,3,…,10的ln ε(k,p)数据进行多维线性回归,得到a=0.264 6±0.007 0,b=0.601 6±0.004 5,c=-33.13±0.08,拟合平面如图 5所示.拟合指标中残差平方和SSE=0.050 99值较小,判定系数R-square=0.999 7非常接近1,可见模型(11)在此k和p值范围内和误差数据符合得很好.
|
| 图 5 并行算法仿真数值误差模型拟合 Figure 5 Model fitting for the numerical error of the parallel algorithm simulation |
为了实现并行算法的一个具体实例,本文基于POSIX线程[20]设计了并行执行的模型.该模型涉及POSIX线程的数据类型条件量pthread_cond_t和互斥量pthread_mutex_t,以及标准函数:
1) pthread_mutex_init: 初始化一个互斥量;
2) pthread_cond_init: 初始化一个条件量;
3) pthread_create: 创建一个新线程;
4) pthread_mutex_lock: 锁住一个互斥量,当互斥量已经处于锁住状态时,调用进程将阻塞直到互斥量变为解锁状态;
5) pthread_cond_broadcast: 解除当前所有被特定条件量阻塞的进程;
6) pthread_mutex_unlock: 解锁一个互斥量;
7) pthread_cond_wait: 原子操作释放指定互斥量并使得调用进程阻塞在条件量上,当函数成功返回之后,互斥量再度锁住并被调用进程所拥有.
并行执行模型的具体实现从MainProcedure开始进入,在创建各个子任务进程之后会随之不断循环执行.设定所需的全局变量:
向量x
pthread_cond_t condDataLoaded
pthread_mutex_t mutexLock
pthread_mutex_t mutexCountFinished
countWaiting=0
countFinished=False
notFinished=False
子任务线程函数ThreadFunc(index,segments)实现的伪代码如下:
while True do
pthread_mutex_lock( & mutexLock)
countWaiting=countWaiting+1
pthread_cond_wait( & condDataLoaded, & mutexLock)
countWaiting=countWaiting-1
sindex=PFHT(x,index,segments)
pthread_mutex_lock( & mutexCountFinished)
countFinished=countFinished+1
if countFinished等于segments then
输出结果∑isi
notFinished=False
countFinished=0
end if
pthread_mutex_unlock( & mutexCountFinished)
end while
主函数MainProcedure实现的伪代码如下:
pthread_mutex_init( & mutexLock,NULL)
pthread_mutex_init( & mutexCountFinished,NULL)
pthread_cond_init( & condDataLoaded,NULL)
对i=0,1,…,segments-1分别创建子任务线程,其中各线程函数为ThreadFunc(i,segments)
while True do
输入x
如果countWaiting<segments则忙等
pthread_mutex_lock( & mutexLock)
pthread_cond_broadcast( & condDataLoaded)
notFinished=True
pthread_mutex_unlock( & mutexLock)
忙等直到notFinished为False
end while
伪代码描述完毕.为了简洁,无限循环的退出条件和资源的释放并没有在伪代码中给出.
具体的代码使用了pthread库在Ubuntu 14.04 LTS上通过gcc 4.8.2编译实现,运行的PC平台拥有Intel Core i5-2410M CPU(2.30 GHz×4)及4 GB内存.实验对比了串行算法单线程实现及双线程并行算法实现(即两个子任务,s=2,p=1)的实际执行时间.计算任务为随机产生的2k长度(其中k取16到25)向量的Hadamard变换.为了减少扰动,将10次Hadamard变换计算作为一组(一次试验),并将得到的计时结果除以10作为该组一次Hadamard变换需要的时间,最后对每一个k值进行1 000次实验.换算出来的一次Hadamard变换耗时的结果以“均值±标准差”的形式给出.并行的效率以并行加速比Sp=Ts/Tp来量化[21],其中Ts为串行算法在CPU一个核上用单线程实现的执行时间,Tp为并行算法在CPU两个核上用双线程实现的执行时间.
因为本文提出的并行算法是基于一种目前广泛应用的成熟串行Hadamard快速变换算法[1, 9]实现的,而据本文作者所知,目前针对Hadamard快速变换并没有其它任务级的并行算法,因此,为了呈现该串行Hadamard快速变换算法的效率,并进一步突出本文提出的并行算法的优化效果,本文使用了算法时间复杂度同为O(n lnn)[16]的快速傅立叶变换目前最新的计算库FFTW(版本3.3.4)[22]在同平台下单线程计算同样长度向量的离散傅里叶变换所需时间Ts-fftw作为对照.Ts-fftw的计算使用了库函数fftw_plan_dft_r2c_1d,计算方法参数选用其默认值FFTW_MEASURE,对于每一个k值,进行1 000次实验,最后求实际耗时的平均值.实验结果如表 1所示.
| k | Ts-fftw/ms | Ts/ms | Tp/ms | Sp |
| 16 | 1.712 | 1.22±0.01 | 1.19±0.01 | 1.02 |
| 17 | 3.690 | 2.72±0.01 | 2.55±0.01 | 1.07 |
| 18 | 8.715 | 7.65±0.02 | 5.91±0.03 | 1.29 |
| 19 | 21.594 | 18.32±0.04 | 13.98±0.07 | 1.31 |
| 20 | 45.118 | 38.10±0.04 | 28.63±0.08 | 1.33 |
| 21 | 90.483 | 80.84±0.07 | 59.92±0.10 | 1.35 |
| 22 | 188.533 | 166.27±0.15 | 120.90±0.15 | 1.38 |
| 23 | 384.748 | 350.75±0.27 | 253.03±0.36 | 1.39 |
| 24 | 743.137 | 723.62±0.56 | 511.46±0.69 | 1.41 |
| 25 | 1 588.359 | 1 515.28±0.62 | 1 066.76±0.81 | 1.42 |
| 注:1) Hadamard快速变换并行算法的子任务数为2,即s=2,p=1.2) 输入向量的长度为2k; Ts和Tp分别表示单线程和双线程实现的实际执行时间; Ts-fftw为作为对照的FFTW库单线程计算同长度向量的傅立叶变换的时间; Sp=Ts/Tp为并行加速比,其值越大则实际并行实现的性能越好.3)Sp随着k的增大而增大,直观的解释是当子任务的计算时间变长,并行开销在Tp中的比例降低了.4)同向量长度下Ts比Ts-fftw稍快的原因是Hadamard快速变换的蝶形运算实现中并不需要乘法. | ||||
本文的重点是设计一种任务级的Hadamard变换的并行算法,如2.2节描述.在单个子任务中,并行开销仅包括扩散阶段的符号函数计算,而这个计算可以用位运算高效地进行.受益于这个结构,该算法可以在多种平台上有简单的实现.然而,这个优点并不意味着在所有应用中,该任务级并行算法一定比指令级并行更优越; 此外,扩散阶段的设计在数学意义上是否为X=Wx并行化的最优方案,仍是一个开放问题.
从实践的角度看,本文提出的并行算法的效率和具体硬件平台是高度相关的,这意味着:
1) reverseBits()和parity()的具体位运算的实现需要根据具体的硬件平台来选择,因为这些不同的实现方法涉及了内存访问(如使用查找表)和耗时算术运算(如使用乘法)之间的权衡.
2) 因为Hadamard变换本身的高效性,本文采用POSIX线程而不是MPI(message passing interface)来描述并行模型.这是因为一方面POSIX线程在多核PC平台上有轻量级的实现; 另一方面在单项素相机的应用背景下,未来考虑的是一种基于硬件(如FPGA)的实现.
3) 表 1中的实验结果会随着软硬件平台的改变而有所不同.因为总的并行开销不仅与扩散阶段有关,而且与所有子任务的同步延迟、所有子任务结果的累加有关,所以并行算法的实际执行时间不一定快于串行算法的时间.本文实验仅仅是提供了一个成功的示例.
6 结论本文提出了一种通用的基二快速Hadamard变换的任务级并行算法.通过对扩散阶段进行构造,并行算法和串行算法结果的等价性得以证明.数值仿真进一步地确认了并行算法结果的正确性,并量化展示了因为浮点运算精度损失带来的误差,提出了误差的经验模型.最后,PC上的POSIX线程实验给出了一种可行的应用示例.实验结果表明,在我们的平台和特定配置之下,对于输入向量长度220~225的问题规模,并行加速比可达到1.33~1.42.
| [1] | Agaian S S, Sarukhanyan H G, Egiazarian K O, et al. Hadamard transforms[M]. Washington, USA: SPIE Press , 2011 . |
| [2] | Horadam K J. Hadamard matrices and their applications[M]. Princeton, USA: Princeton University Press , 2007 . |
| [3] | Rezaul B, Daniel T, Lai H, et al. Computational intelligence in biomedical engineering[M]. Boca Raton, USA: CRC Press , 2007 . |
| [4] | Evangelaras H, Koukouvinos C, Seberry J. Applications of Hadamard matrices[J]. Journal of Telecommunications and Information Technology, 2003, 2 : 3–10. |
| [5] | Wallis W D. Introduction to combinatorial designs[M]. Boca Raton, USA: Chapman & Hall/CRC Press , 2007 . |
| [6] | Nakahara M, Ohmi T. Quantum computing[M]. Boca Raton, USA: CRC Press , 2008 . |
| [7] | Takhar D, Laska J N, Wakin M B, et al. A new compressive imaging camera architecture using optical-domain compression[C]//Electronic Imaging 2006. |
| [8] | Qin S J, Bi S, Xi N. Maximum length sequence encoded Hadamard measurement paradigm for compressed sensing[C]//2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM). Piscataway, NJ, USA: IEEE, 2014: 1151-1156. |
| [9] | Li C. An efficient algorithm for total variation regularization with applications to the single pixel camera and compressive sensing[D]. Houston, Texas, USA: Rice University, 2009. |
| [10] | Yu H, Liu Y, Peng Y, et al. A portable single-pixel camera based on coarse-to-fine coding light[C]//2015 IEEE International Conference on Imaging Systems and Techniques (IST). Piscataway, NJ, USA: IEEE, 2015: 1-5. |
| [11] | Rousset F, Ducros N, D′Andrea C, et al. Single pixel camera: An acquisition strategy based on the non-linear wavelet approximation[C]//2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). Piscataway, NJ, USA: IEEE, 2015: 6240-6243. |
| [12] | Sghaier M, Abdelkefi F, Siala M, et al. Single-Pixel-Camera paradigm for multiband cooperative sensing in cognitive radio systems[C]//2015 IEEE 81st Vehicular Technology Conference (VTC Spring). Piscataway, NJ, USA: IEEE, 2015: 1-5. |
| [13] | Chen H, Xi N, Song B, et al. Single pixel infrared camera using a carbon nanotube photodetector[C]//2011 IEEE Sensors. Piscataway, NJ, USA: IEEE, 2011: 1362-1366. |
| [14] | Chan W L, Charan K, Takhar D, et al. A single-pixel terahertz camera[C]//2008 CLEO/QELS Conference on Quantum Electronics and Laser Science. Piscataway, NJ, USA: IEEE, 2008: 1-2. |
| [15] | Golbabaee M, Vandergheynst P. Joint trace/TV norm minimization: A new efficient approach for spectral compressive imaging[C]//2012 19th IEEE International Conference on Image Processing (ICIP). Piscataway, NJ, USA: IEEE, 2012: 933-936. |
| [16] | Sedgewick R, Wayne K. Algorithms[M]. Boston, USA: Addison-Wesley Professional , 2011 . |
| [17] | Horn R A, Johnson C R. Matrix Analysis[M]. 2nd ed. New York, USA: Cambridge University Press , 2013 . |
| [18] | Henry J, Warren S. Hacker's delight[M]. 2nd ed. Boston, USA: Addison-Wesley . |
| [19] | Henry J, Warren S. Hacker's delight[M]. 2nd ed. Boston, USA:Addison-Wesley, 2013. |
| [20] | IEEE Std 754-2008. IEEE standard for floating-point arithmetic[S]. |
| [21] | 张林波, 迟学斌, 莫则尧, 等. 并行计算导论[M]. 北京: 清华大学出版社 ,2006 : 223 -238. Zhang L B, Chi X B, Mo Z R, et al. Introduction to parallel computing[M]. Beijing: Tsinghua University Press , 2006 : 223 -238. |
| [22] | Zhang L B, Chi X B, Mo Z R, et al. Introduction to parallel computing[M]. Beijing:Tsinghua University Press, 2006:223-238. |
| [23] | The FFTW Release Notes:FFTW 3.3.4[EB/OL]. (2014-03-16)[2015-03-12] http://www.fftw.org/release-notes.html. |



