1 引言
目前在实际生产中,焊接机器人的路径规划主要通过示教编程、多次的人工操作来优化路径,不仅示教过程效率低下,而且示教结果也很难保证焊接效率及焊接质量.当焊接任务的焊点较多时,路径规划的研究可以很大程度上提高焊接效率,国内外学者对路径长度的研究较多,Wang人[1]提出了GA-PSO算法以解决双机器人路径问题,其优化目标为路径长度.Chettibi[2]提出了一种轨迹规划器来处理机器臂的路径规划中的能耗问题.文[3]提出了一种改进的A*算法的动态路径规划算法能够使机器臂避开动态的障碍物.文[4]用一种新的方案以解决6自由度工业机器人无奇异路径规划.Yang[5]用一种新型的基于TSP(travelling salesman problem)的弹性网络和神经网络来解决点焊机器人路径规划中的变形问题.而在实际应用中,需要同时考虑多个焊接影响因素,本文将路径长度及能耗作为优化目标对焊机机器人进行路径规划.
当求解多目标组合优化问题时,群智能优化算法显示出了巨大的优点.其中常用的群智能优化算法有遗传算法、粒子群算法、蚁群算法等.粒子群算法因其收敛速度快和算法结构简单等优点,自提出之后便得到了广泛的应用.在用粒子群算法求解多目标优化问题中,不同的指导粒子选择策略会使算法的优化性能有很大的不同.Hu等[6]提出的动态邻域PSO算法求解多目标问题,对两个目标逐步计算粒子邻域内适应度较好的粒子,将其作为该粒子的指导粒子.文[7-8]指导粒子的选取策略为在所得到的外部档案中的非劣解中随机选取一个.与上述二者相比,不少学者为了均衡各个区域的搜索概率,基于非劣解在目标空间的密度来选取粒子.如Coello[9]采用网格法度量密度,Reddy[10]采用相邻非劣解之间的欧几里得距离求得,向长城等[11]则采用小生境方法作为密度的评价指标,Mostaghim等[12]提出了Sigma方法来选择指导粒子.以上算法的指导粒子选择方法都是基于目标空间进行选择,然而,当优化问题真实Pareto前沿在决策空间不连贯、非线性时,这些指导粒子策略很大程度上会导致大部分粒子在决策空间远离Pareto前沿的区域搜索,不利于接近Pareto前沿,导致搜索效率很低.文[13]提出了一种新型基于决策空间的指导粒子选择策略兼顾了局部和全局搜索能力,当优化问题真实Pareto前沿在决策空间不连贯、非线性时,该算法的优化效果异常明显.然而该算法针对的是连续空间的多目标优化问题,而实际运用中大多数是离散多目标优化问题,如TSP问题、生产调度等.本文对该算法提出改进,以使其适用于解决离散多目标优化问题.
2 焊接机器人路径规划问题模型本文分析路径规划时考虑路径长度和能耗两个优化指标.路径规划指的是焊接机器人的焊点顺序规划,然而在分析路径长度和能耗时又涉及到机器人的运动学与动力学,这时便需要分析焊点之间的轨迹规划问题.因此本文的数学模型分为整体和局部,整体为TSP问题,局部(两个焊点之间)为轨迹规划问题.
在算法的开始,初始化随机产生焊点的焊接顺序,然后再对焊接顺序上前后两个焊点之间进行轨迹规划,进而得到焊接路径长度及能耗.然后根据这两个适应度来选择非劣解进行算法迭代.最后在运用粒子群算法求得非劣解基础上,根据生产需要,选定合适的权重,即可得到符合生产需求的焊点顺序.
2.1 路径长度分析旅行商问题(TSP)是一个复杂的组合优化问题,群智能算法在对组合优化问题的解决方面显示了比较好的优化效果[14].TSP问题描述: 旅行商必须对每个城市访问一次,并且最终返回到开始的城市.假定N个城市点的集合{v1,v2,…,vN},cki,j是城市vi、vj之间的花费,TSP的优化目的为[15]
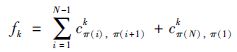
|
(1) |
若k=1,则为单目标TSP,通常指两个城市之间的距离; 若k>1,则为多目标TSP.如果ci,jk=ci,jk,则为对称TSP问题,否则为不对称TSP问题.
本文对焊接问题进行了简化,焊接过程中的提枪、进枪动作及焊枪与工件的避障问题未考虑在内.当机器人在执行操作时,各个关节必须协调运动,因此必须使关节的角速度、角加速度连续变化,若发生突变,将会给机器人带来冲击,因此要进行轨迹规划.轨迹指机器人操作臂在工作过程中的位移、速度和加速度.工业机器人的轨迹规划可以分为点到点(point to point)运动和轨迹跟踪(trajectory tracking)运动.轨迹规划可以在关节空间进行,也可以在笛卡尔空间进行,由于本文的目标为点与点之间的规划,不需要轨迹跟踪,并且关节空间轨迹规划简单,不存在机器人机构奇异点问题,因此本文选择关节空间的轨迹规划.
本文采用五次多项式插值算法进行关节空间轨迹规划,通过6个约束条件: 初始位置的关节角位移θ0、终止位置的关节角位移θn、初始位置的关节角速度${{\dot{\theta }}_{0}}=0$、终止位置的关节角速度${{\dot{\theta }}_{n}}=0$、初始位置的关节角加速度${{\ddot{\theta }}_{0}}=0$终止位置的关节角角速度${{\ddot{\theta }}_{n}}=0$,即可求解五次多项式θ(t)=K0+K1t+K2t2+K3t3+K4t4+K5t5,得到各个关节参数关于时间的函数: 关节角度函数θ(t)、角速度函数$\dot{\theta }\left( t \right)$、角加速度函数$\ddot{\theta }\left( t \right)$.
在求解路径长度时,当两个焊点之间的轨迹规划完成之后,焊枪在两个焊点之间的角位移方程θ(t)为已知的连续曲线,由于机器人的关节空间曲线与笛卡尔空间的曲线并不是连续对应关系,因此不能直接得出焊枪末端的笛卡尔空间运动曲线.然而正运动学可以求解笛卡尔空间某个时刻焊枪的位姿,因此本文以近似的直线长度来代替实际笛卡尔空间的路径长度的方法求解焊枪的路径.具体方法为: 以时间为分割单位将笛卡尔空间的路径曲线分为多个小区间,随着分割区段数量的增加,近似直线长度逐渐接近实际笛卡尔空间的路径长度,当区段数量达到一定值时,近似长度和实际长度之差可以忽略不计.焊点之间的路径长度为
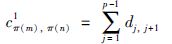
|
(2) |
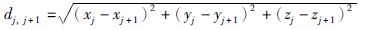
|
(3) |
其中,cπ(m),π(n)1为焊点m和n之间的路径长度.当计算cπ(m),π(n)1时,将焊点m和n之间的轨迹分为p段,dj,j+1为第j个区间两端过渡点(xj,yj,zj)、(xj+1,yj+1,zj+1)之间的直线距离,(xj,yj,zj)、(xj+1,yj+1,zj+1)可运用运动学正问题由关节角θ(t)通过坐标转换变为笛卡尔空间坐标.
2.2 能耗分析机器人动态性能由动力学方程描述,研究机器人运动与关节力(力矩)间的动态关系.机器人动力学要解决两类问题:
动力学正问题是根据关节驱动力矩或力,计算机器人的运动(关节位移、速度和加速度); 动力学逆问题是已知关节的位移、速度和加速度,求出所需要的关节力矩或力.对机器人动力学的研究,所采用的方法很多,有拉格朗日(Lagrange)方法、牛顿—欧拉(Newton-Euler)、高斯(Gauss)、凯恩(Kane)等方法.拉格朗日动力学则是基于系统能量的概念,以简单的形式求得非常复杂的系统动力学方程,并具有显式结构,物理意义比较明确[16].
(1) 拉格朗日函数
对于任何机械系统,拉格朗日函数L定义为系统总的动能Ek与总的势能Ep之差,即:
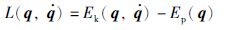
|
(4) |
式中,q=[q1,q2,…,qn]表示动能与势能的广义坐标,$\dot{q}=\left[ {{{\dot{q}}}_{1}},{{{\dot{q}}}_{2}},\cdots ,{{{\dot{q}}}_{n}} \right]$为相应的广义速度.
(2)机器人系统动能
在机器人中,连杆是运动部件,连杆i的动能Eki为连杆质心线速度引起的动能和连杆角速度产生的动能之和,即:
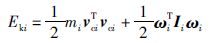
|
(5) |
系统的动能为n个连杆的动能之和,即:
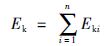
|
(6) |
由于vci和ωi是关节变量q和关节速度$\dot{q}$的函数,因此,从式(6)可知,机器人的动能是关节变量和关节速度的标量函数,记为${{E}_{\text{k}}}\left( q,\dot{q} \right)$,可表示成
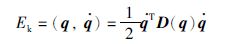
|
(7) |
式中,D(q)是n×n阶的机器人惯性矩阵.
(3) 机器人系统势能
设连杆i的势能为Epi,连杆i的质心在O坐标系中的位置矢量为pci,重力加速度矢量在坐标系中为g,则:
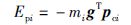
|
(8) |
机器人系统的势能为各连杆的势能之和,即:
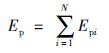
|
(9) |
它是q的标量函数.
(4) 拉格朗日方程
系统的拉格朗日方程为
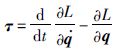
|
(10) |
上式又称为拉格朗日—欧拉方程,简称L-E方程.式中,τ是n个关节的驱动力或力矩矢量,上式可写成:
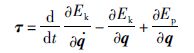
|
(11) |
针对6自由度的关节机器人逆运动学问题,因为其结构参数多、解具有非线性和耦合性,并且需要求解代数方程等,因此求解比较困难[17].本文的轨迹规划采用关节空间的轨迹规划,在计算轨迹过程中,运用Matlab的机器人工具箱(robotics toolbox)对6自由度的关节机器人进行逆运动学分析.本研究运用D-H坐标系理论,分析该机器人的运动学问题,并在运动学分析的基础上,在关节空间采用五次多项式函数插值法,研究机器人轨迹规划的问题.
Step 1 轨迹求解: 根据两点的焊枪位姿,求出各关节位于两点时的关节角度.运用五次多项式求解出中间点各关节中间点向量,并得出关节角、关节角速度、关节角加速度关于时间t的中间点向量.
Step 2 运用逆动力学求解出个关节力矩.
Step 3 计算两点间的耗能.根据式(12)求出机器人在两点之间的能耗.能耗公式:
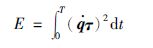
|
(12) |
其中,E为能耗,${\dot{q}}$关节速度,τ为关节力矩.
离散化能耗公式为
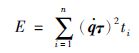
|
(13) |
Step 4 根据焊点顺序,将所有焊点之间的能耗相加即为该路径下总能耗.
3 改进多目标粒子群优化算法 3.1 粒子群算法基本原理基于对鸟群捕食活动的规律性的启发,1995年Kennedy和Eberhart首次提出了粒子群优化(particle swarm optimization,PSO)[18]算法.在PSO算法对鸟群捕食行为的模拟中,每只鸟被命名为一个没有质量和体积的粒子,多个粒子共存、合作寻优.每个粒子根据其自身及群体其它粒子的经验,在问题空间中向更好的位置“飞行”.粒子个体在飞行过程所经历过的最好位置称为个体极值(pBest),整个群体目前所经历过的最好位置称为全局极值(gBest).粒子状态用D维速度vi=(vi1,vi2,…,viD)和位置Xi=(xi1,xi2,…,xiD)表示,则每个粒子根据式(14)、式(15)更新自己的状态,从而产生下一代群体.
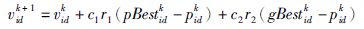
|
(14) |

|
(15) |
式中,k为当前迭代次数; c1 、c2是学习因子(又称加速因子),通常为正数,调节在自身最优位置和全局最优位置的牵引力度; r1、r2是介于0和1之间的随机数.
PSO算法在优化连续问题时显示出来优越的性能,但在解决TSP等离散问题时,原始的PSO算法并不适用,需要对原始PSO算法改进方可应用.Kennedy和Eberhart于1997年提出了一种二进制粒子群优化算法(binary PSO,BPSO)[19],用概率选择参数来实现粒子在空间中的移动.Parsopoulos[20]对PSO算法产生的连续解进行近似取整运算,以取整之后的解来计算适应值,粒子的位置和速度更新公式依旧沿用连续PSO算法.Clerc[21]在求解TSP问题时提出了TSP-DPSO算法.该算法通过对粒子位置和速度矢量的操作,实现了连续粒子群向离散空间的映射.
3.2 多目标粒子群算法TC-MOPSO离散化(1) 三态协调搜索指导粒子选择策略离散化
传统的指导粒子选择策略均是基于目标空间进行选择,文[13]所提出的三态指导粒子选择策略,基于决策空间将所有的粒子分为受约束粒子和不受约束粒子,然后根据粒子激发机制将受约束粒子分为激发态粒子和非激发态粒子.最终将所有粒子分为3种状态: 不受约束状态、激发态、非激发态,不同状态的粒子选择不同的指导粒子选择策略.
TC-MOPSO算法在对受约束粒子及不受约束粒子分类中运用聚类的未加权平均距离法将决策空间按区域划分.各个区域的中心是根据该区域所包含的所有非劣解坐标值的平均值所求出,然后求得各个区域中心间的欧几里得距离,同时计算出各个粒子与各个区域中心的欧几里得距离,找出与粒子最近的区域,若该粒子与该区域小于某个值,则该粒子为该区域的受约束粒子,否则为不受约束粒子.由于TC-MOPSO的区域划分、受约束粒子和不受约束子分类方法均是根据3维坐标空间的欧几里得距离进行运算,然而在求解离散多目标优化问题时,粒子的位置不是用三维坐标来表示,而是用一组序列来表示,此时TC-MOPSO算法便失效.因此应该重新定义粒子间距离、区域划分、受约束粒子和不受约束子分类方法.
粒子间距离的重新定义.在TC-MOPSO算法中,粒子间决策空间的距离定义为两个粒子坐标空间的欧几里得距离,在求解组合优化问题时,粒子的位置为一组排列序列,因而需要重新定义粒子间在决策空间的距离: 将含有不同的边数作为衡量两个路径的距离,不同的边数越多,两个路径的距离就越大.粒子间距离公式为
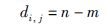
|
(16) |
其中,di,j为粒子i和粒子j的距离,n为TSP问题的城市数量,m为粒子i和粒子j的具有的相同的边数.例如粒子a=[1,2,3,4,5,6,7,8],粒子b=[1,2,3,4,5,6,8,7],则a、b间的距离为2.
受约束粒子和不受约束粒子分类.根据前一次迭代所得到的非劣解,运用聚类算法的最短距离法将决策空间划分区域,并编号Region1~Regionm,然后计算各个粒子距离各个区域的距离.计算某粒子i与区域q的距离dRi,q时,将该粒子与该区域内的所有非劣解的最小距离作为该粒子与该区域的距离.找出与该粒子最近的区域p,如果该粒子与该区域的距离小于某个阈值dthreshold,则该粒子为区域p的受约束粒子.反之,该粒子为不受约束粒子.
不受约束粒子的指导粒子在所有的非劣解目标空间距离排序靠前10%的非劣解中随机选择(全局选择策略),若将所有受约束粒子的指导粒子在其所在的聚类区域中的非劣解中随机选择(区域选择策略),随着算法的迭代可能会使一些决策空间区域内部粒子过多,其它区域内的粒子则相对过少,因而这些区域的搜索概率相应会降低,因此应采取措施平衡各个区域的搜索概率,该算法采取一种粒子激发机制以解决这个问题.
TC-MOPSO算法中的粒子激发机制可以动态地调整各个非劣解附近的搜索粒子数量,以平衡各个区域的搜索概率.原理: 当某个区域中的非劣解数量过少时,若使非劣解数量和搜索概率一致导致,则该区域的搜索粒子数量过少,使该区域的搜索陷入停滞状态,因而在非劣解过少的区域中,适当增加搜索粒子可以提高算法平衡各个区域的搜索概率.粒子激发机制具体步骤如下:
计算各个区域的粒子激发值ratio:
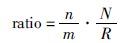
|
(17) |
其中,n为该区域所含非劣解个数,m为该区域所含受约束粒子的个数,N为种群规模,R为外部档案上限.对于每个受约束粒子,若rand<ratio(rand为0~1之间的随机数),则该粒子属于非激发态粒子,否则该粒子被激发为激发态粒子.非激发态粒子指导粒子选择策略为区域选择策略,激发态粒子指导粒子选择策略为全局选择策略.式(17)是为了平衡各个区域的搜索概率,当m、n、R均达到上限时,m=N,n=R,此时ratio的值为1.在正常情况下,ratio的值均为小于1大于0的数,ratio的值随着n的增大而增大,随着m的增大而减小.这便满足了当某区域的n值较大时,该区域就存在较多的潜在的非劣解,此时ratio值的增大有利于增大该区域的搜索概率; 而当m值较大时,说明该区域存在过多的搜索粒子,减小ratio的值有利于该区域的受约束粒子转化为激发态粒子,跳出该区域的搜索,转而搜索其它区域.从而实现了平衡各个区域的搜索概率的期望.对于激发值的判断值设置采用随机数而不采用一个固定的值原因如下: 粒子激发机制整体上受控于ratio值,单次的激发机制具有随机性,是因为用一个随机数可以使粒子转变为激发态依一定的概率进行,ratio值越大越有可能触发激发机制,使算法处于动态平衡,可以防止算法陷入局部最优.若以固定值来判断粒子是否激发,由于不能确定算法在迭代过程中的ratio值,若固定值设置过大,则有可能使所有粒子变为激发态粒子,若固定值设置过小,则有可能所有粒子均不会成为激发态粒子,这两种情况都不利于平衡算法的寻优能力.
但是,由于ratio的值严格受控于n和m的值,当某些区域的n值过小,按其比例会分配非常少的粒子在该区域进行搜索,此时群智能算法的协同优化特点便会在该区域失效,为了解决这个问题,对式(17)进行了改进,见式(18):
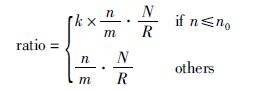
|
(18) |
当某个区域的非劣解数量n小于n0时,将该区域的粒子激发值增大k倍,可以减小该区域的受约束粒子转化为激发态粒子,从而使这些粒子依然在该区域搜索.
对于n0和k值的设置,理论值范围是n0∈[1,R],k>1.二者相互配合可以达到较好的局部与全局搜索效果,在一定范围内的变化并不会对算法有明显的影响.由于不同的测试函数所含有的真实Pareto解的分布情况不同,若分布较为均匀,则这两个参数的设置基本没有影响.因此当R为100,n0的值设为2,k值设为4可以满足大部分测试函数.由于文中的指导粒子选择策略的机理,如果阈值过大,算法的局部搜索能力便会增强,全局搜索能力减弱; 如果阈值过小,全局搜索能力便会增强,局部搜索能力减弱.本文的阈值dtresold设为TSP问题排序个数的一半.
综上所述,三态指导粒子选择策略为: 先将所有粒子分为两类,受约束粒子和不受约束粒子.远离所有区域的粒子为不受约束粒子,靠近某个区域的粒子为受约束粒子.然后运用粒子激发机制将受约束粒子分为2类: 激发态和非激发态粒子.激发态和不受约束的粒子指导粒子选择策略为在全局选择策略; 非激发态粒子的指导粒子选择策略为区域选择策略.
(2) 改进外部档案保存机制
原算法对传统外部档案的改进在减小计算复杂度的同时又尽可能提高非劣解分散性.因而在求解多目标离散问题时,该方法依然有效.
3.3 DTC-MOPSO算法具体实现步骤根据以上算法的描述,离散化三态协调搜索多目标粒子群算法(DTC-MOPSO)详细步骤如下:
Step 1 初始化.初始化参数,初始化种群各个粒子的位置和速度及个体历史最优值.
Step 2 运用Pareto支配方法,找出非劣解集并将其存储在外部档案中,计算非劣解基于目标空间的距离.
Step 3 为每个粒子寻找指导粒子.如果非劣解数量不大于20,在非劣解集中随机选择一个非劣解作为其指导粒子; 如果非劣解数量大于20,运用三态指导粒子选择策略为其寻找指导粒子.
Step 4 运用式(14)、式(15)更新每一个粒子的位置和速度,评估粒子的适应度,根据适应度更新粒子的个体历史最优.
Step 5 将外部档案的非劣解和当前迭代的粒子放入一个暂时的档案中,运用Pareto支配方法,找出暂时的档案中的非劣解集,并将其储存在外部档案中,计算非劣解的密度.若外部档案规模超出上限,运用本文提出的外部档案保存机制,保留R个非劣解.
Step 6 应用突变因子,在当前的迭代粒子中依概率产生突变.
Step 7 增加迭代次数t,若t<Tmax,跳到Step 4; 否则终止迭代,输出外部档案中的解作为最终解.
3.4 算法性能测试及分析本文选择DTC-MOPSO、EM-MOPSO(elitist-mutated MOPSO)[7]及Deb提出的解决多目标问题的遗传算法NSGA-Ⅱ[22]进行比较.通过对100个点的TSP双目标问题进行求解,采用GD(代距)、SP(分散性指标)及t(运行时间)三个性能评价指标来分析新算法DTC-MOPSO的性能.
3.4.1 性能评价准则学者们对多目标优化算法的性能测试提出了各种评价准则,本文运用了其中的3个评价准则来评价算法的优劣.同时也加入了算法的运行时间对算法的复杂度进行评价.
(1) GD(代距).这个标准用来描述算法所获得的非劣解与问题的真实Pareto前端之间的距离.
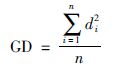
|
(19) |
其中,n为算法所得非劣解的个数,di为第i个解到真实Pareto最优解集的最小欧几里得距离(在目标向量空间).
若GD=0,表示所得非劣解均属于Pareto最优解集.该指标反映算法所得优化解集的与Pareto最优解的逼近程度.
(2) SP(分散性).该指标描述非劣解在目标空间上的分布范围.
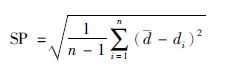
|
(20) |
式中,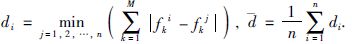
(3) t(运行时间).该指标为算法迭代最大次数所需要的时间,可以一定程度上反应算法的计算复杂度.
3.4.2 测试数据及参数设置测试用例选择100个城市的TSP问题,目标为双目标.城市间花费在1~100之间的整数中随机产生.在算法比较中,测试用例保持不变.
当测试不同的多目标算法的性能时,真实Pareto解需要已知.但是,对多目标优化而言,真实Pareto解并不容易求得.本文用近似Pareto解代替真实Pareto解,具体近似Pareto解的求法为: 先将各种算法多次求解的非劣解放在一个档案中,然后根据Pareto支配原则,并根据在目标空间的分散性及多样性,从这个档案中求出一定数目的非劣解作为近似Pareto解.本文的算法求解次数为每种算法单独运行50次,近似非劣解数目为50.
3种算法的种群规模均为100,DTC-MOPSO、EM-MOPSO的外部档案规模为100,NSGA-Ⅱ的精英解集规模为100.3种算法在求解测试函数时迭代100次.DTC-MOPSO的区域划分系数为0.1,学习因子C1为1.0,学习因子C2随着迭代从0.5线性递增到1.5,收缩因子为0.9,惯性权重为0.4.EM-MOPSO学习因子C1、C2为1.0,惯性权重为0.4,分格数为30,突变因子的参数与原文一致.EM-MOPSO的学习因子C1、C2分别为1.0、0.5; 收缩因子为0.9; 惯性权重为0.4; 在突变过程中,突变粒子数为15,Pem为0.2; 突变范围mutScale随着迭代从0.2线性递减到0.01.NSGA-Ⅱ为实数编码,交叉和突变因子ηc、ηm均为20,突变池规模为原始种群规模的一半.3种算法运算编程采用相同的编程习惯,每个算法独立运行20次,统计各个算法评价指标的均值和方差.测试环境为: CPU: Intel(R)Core(TM)i5-3210M CPU@2.50 GHz; 内存: 4.00 GB; 操作系统: 64位Windows 7; 运行平台: Matlab 2014a.
3.4.3 算法测试结果与分析根据以上设置,求得算法的各种性能指标如表 1所示,其中较好的数据在表中加黑表示.
| 算法 | GD | SP | t | |||||||||
| min | max | std | mean | min | max | std | mean | min | max | std | mean | |
| NSGA-Ⅱ | 146.43 | 243.40 | 29.95 | 199.46 | 54.86 | 264.07 | 57.05 | 110.78 | 203.46 | 219.77 | 3.40 | 209.33 |
| EM-MOPSO | 59.50 | 108.79 | 15.16 | 84.67 | 16.99 | 60.01 | 11.37 | 33.25 | 22.510 | 22.76 | 0.06 | 22.62 |
| DTC-MOPSO | 22.10 | 68.73 | 12.10 | 51.64 | 8.35 | 39.84 | 9.88 | 20.81 | 36.194 | 37.99 | 0.44 | 37.15 |
收敛性分析: 从表 1中的3种算法GD数据可以得出改进算法的GD均值及标准差值均小于另外两种算法.DTC-MOPSO算法收敛性优于NSGA-Ⅱ算法,是因为改进的PSO算法可以很好地协调整体和局部搜索,使算法的搜索不断地向真实的Pareto前沿搜索,不断地接近Pareto前沿.而NSGA-Ⅱ虽然局部搜索能力较好,但全局搜索能力较差,因而易陷入局部最优.DTC-MOPSO算法收敛性优于EM-MOPSO,是由于DTC-MOPSO算法采用新型的指导粒子选择策略可以增大在非劣解前沿的搜索效率,同时兼顾全局搜索能力,因而收敛性优于后者.
多样性分析: 从表 1中的3种算法的SP数据可以得出DTC-MOPSO算法的分散性远远优于另外2种算法.原因在于DTC-MOPSO算法不但很好地协调了全局与局部搜索能力,同时采用的改进外部档案保存机制可以使每次保存的非劣解均匀地分布于目标空间.
复杂度分析: 从表 1中3种算法运行时间可以看出,改进算法的时间略微大于EM-MOPSO算法,远远小于NSGA-Ⅱ算法,这是因为,与EM-MOPSO算法相比,改进算法在三态协调指导粒子选择策略及外部档案在保存非劣解时均花费了时间.
综上所述,DTC-PSO仅仅运用了比EM-MOPSO算法稍微多的时间代价,而所取得的算法收敛性以及分散性均远远优于EM-MOPSO算法.而无论在收敛性、分散性还是算法复杂度方面均优于NSGA-Ⅱ算法.
4 焊接机器人多目标路径规划 4.1 优化对象分析本文优化对象为汽车白车身焊接点焊顺序规划.如图 1所示为双机器人点焊位置分布,具体坐标见表 2.本文只考虑单个机器人的路径规划,优化目标为简化的路径长度及能耗.焊接机器人选型为安川机器人ES165D.
|
| 图 1 白车身焊点分布 Figure 1 The distribution of body-in-white′s spots |
| 序号 | X | Y | Z |
| 1 | 1 929.14 | -600.142 | 666.876 |
| 2 | 1 934.11 | -639.345 | 665.808 |
| 3 | 1 934.69 | -678.812 | 664.171 |
| 4 | 1 934.85 | -719.019 | 663.651 |
| 5 | 1 695.41 | -607.300 | 715.673 |
| 6 | 1 690.48 | -622.294 | 701.080 |
| 7 | 1 694.94 | -646.784 | 715.807 |
| 8 | 1 690.08 | -666.503 | 701.601 |
| 9 | 1 694.47 | -686.470 | 715.941 |
| 10 | 1 689.67 | -710.712 | 702.123 |
| 11 | 1 605.39 | -574.233 | 607.257 |
| 12 | 1 625.86 | -582.701 | 617.580 |
| 13 | 1 628.7 | -601.829 | 628.843 |
| 14 | 1 629.22 | -633.532 | 643.024 |
| 15 | 1 629.53 | -662.358 | 652.834 |
| 16 | 1 629.23 | -720.474 | 668.215 |
| 17 | 1 511.18 | -605.947 | 579.883 |
| 18 | 1 511.48 | -641.282 | 592.229 |
| 19 | 1 512.02 | -670.893 | 603.626 |
| 20 | 1 511.86 | -729.171 | 616.430 |
工业机器人轨迹规划的研究和控制对于提高工业机器人的工作效率起着十分重要的影响[23].在能耗计算过程中必须要对机器人进行轨迹规划.轨迹规划过程分为正运动学分析和逆运动学分析.其中,正运动学为根据各个关节角度求解机器人末端位姿.机器人的逆运动学分析指机器人的末端笛卡尔空间到关节空间的映射方法,得到运动学逆解,便可以用于机器人的末端笛卡尔空间的位姿控制.也就是已知机器人末端执行器相对于机器人基座的位置和位姿,计算出满足要求的关节角、关节加速度.然后求解动力学逆解,根据关节角、关节加速度求出关节力矩.
本文用Matlab机器人工具箱对机器人的运动学及逆运动学及逆动力学进行分析并求出能耗.首先求出任意两个焊点之间的能耗,然后根据焊点顺序,将所有路径上的焊点间能耗相加即得出中能耗.整体优化过程如下:
1) 用Link函数根据每个关节的DH参数[θ d a α]生成对应的关节连杆框架.
2) 用SerialLink函数根据各个关节的Link函数对目标机器人建立完整的数学模型.
3) 根据平移向量和欧拉角的构造变换矩阵的函数,如transl、trotx、troty和trotz,生成对应的变换矩阵.
4) 用ikine函数采用数值解法计算对应于齐次变换矩阵的关节角.
5) 根据jtraj函数求得运动学逆解即关节角、关节加速度、关节加加速度.
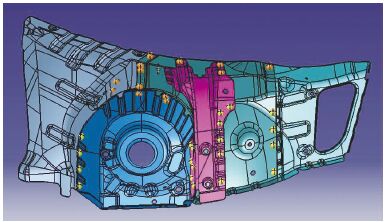
6) 用逆动力学求解函数rne求出各个关节的力矩; 根据能耗公式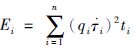
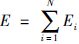
7) 根据ikine函数计算焊枪各个时刻位于笛卡尔空间的位置,计算两个焊点之间的近似路径长度.根据焊接顺序计算整个路径长度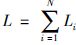
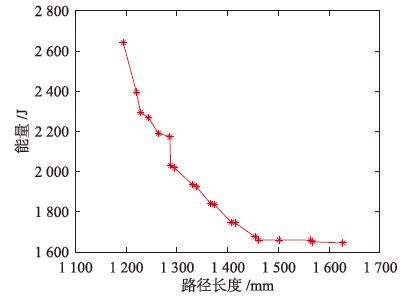
将以上计算路径长度和能耗运用到多目标优化算法适应度计算中,初始种群数量设置为200,迭代次数为300,外部档案规模为20.随机优化初始种群路径,算法迭代300次后所求的非劣解如图 2所示.本文的两个焊点之间的区段数量设为50.
|
| 图 2 焊接机器人路径规划Pareto解 Figure 2 The Pareto solutions of welding robot path planning |
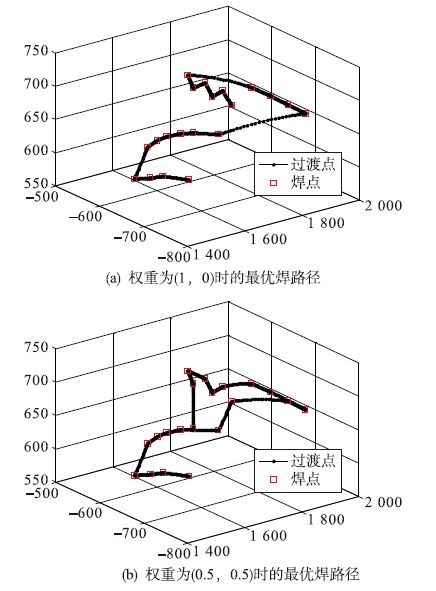
多目标非劣解求解目的是为不同的生产权重提供依据,在实际生产中,在生产中的权重是一定的.当两个目标权重为(1,0),最优焊接路径为: 16→9→8→6→5→7→1→2→3→4→10→15→14→13→12→11→17→18→19→20.如图 3(a)所示,路径长度和能耗分别为1 197.11 mm、2 645.92 J.当两个目标权重为(0.5,0.5),最优焊接路径为: 15→6→5→7→8→9→1→2→4→3→10→15→14→13→12→11→17→18→19→20,如图 3(b)所示,路径长度和能耗分别为1 337.04 mm、1 931.01 J.
|
| 图 3 不同权重时的最优焊点路径 Figure 3 The optimal path of spots of different weights |
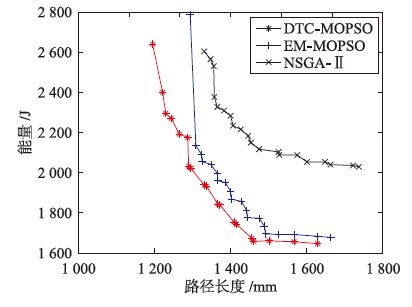
在实际生产过程中,根据生产需求,首先确定两个目标的权重,然后从所得的非劣解中选取最优值,即可得出此时的最优路径.本文将DTC-MOPSO与另外两种算法所得出的非劣解进行比较,3种算法初始种群数量设置为200,迭代次数为300,外部档案规模为20,其余参数设置参照本文3.4.2节.3种算法优化结果见表 4.其中加黑的数据为优化结果较好的部分.图 4为3种算法某次所得的非劣解在目标空间的分布.
| 算法 | GD | SP | t | |||||||||
| min | max | std | mean | min | max | std | mean | min | max | std | mean | |
| NSGA-Ⅱ | 121.45 | 321.02 | 95.24 | 213.39 | 23.29 | 146.29 | 36.10 | 35.93 | 82.32 | 135.87 | 17.97 | 113.51 |
| EM-MOPSO | 135.92 | 215.62 | 70.61 | 243.65 | 6.90 | 104.71 | 21.22 | 29.41 | 8.00 | 8.93 | 0.29 | 8.43 |
| DTC-MOPSO | 125.58 | 205.84 | 90.42 | 178.77 | 8.15 | 43.45 | 5.36 | 26.66 | 8.19 | 9.74 | 0.45 | 8.92 |
|
| 图 4 3种算法所获得的路径规划Pareto解 Figure 4 The Pareto solutions of path planning generated by three algorithms |
从表 4可以看出3种算法求得的多目标焊接机器人路径非劣解的优劣.DTC-MOPSO算法所得的非劣解与另外两种算法相比,更接近真实非劣解前沿.DTC-MOPSO算法所得的非劣解在收敛性上略微好于NSGA-Ⅱ,远远优于EM-MOPSO所得的非劣解.同时图 4也显示出DTC-MOPSO算法比其它两种算法更接近Pareto前沿.由于优化对象仅有20个点,复杂度远远低于前文100个点的复杂度,因而DTC-MOPSO算法的优化效果不如前文那么明显.同时,粒子群算法的外部档案保存的为非劣解,而NSGA-Ⅱ的外部档案采用非支配排序方法,不仅保存了非劣解,同时也保存了次优解.当优化问题复杂度较低时,非劣解数量减少,此时NSGA-Ⅱ的非支配排序法的效果要优于粒子群算法的外部档案方法,但这同时是以牺牲时间为代价的.当优化问题的复杂度较大时,在算法迭代到一定程度后,非劣解便达到外部档案的上限,此时NSGA-Ⅱ的非支配排序法进行排序已是多余之举,而DTC-MOPSO算法仅保存非劣解的方法不仅足以到达指导粒子进行搜索,同时也降低了运算复杂度.
对于所得非劣解的分散性而言,DTC-MOPSO算法同样优于其他两种算法,这是因为,只要在算法迭代过程中,所得的非劣解超过外部档案规模时,便要进行剔除动作,只要有剔除动作,便可以体现改进算法的优势.但是随着求解问题复杂度的降低,改进算法的分散性优势会降低.这是因为剔除的次数越多,DTC-MOPSO算法的优势就越明显,反之,其优势就会减弱.当所求问题的非劣解始终没有达到外部档案的上限时,DTC-MOPSO算法的外部档案保存策略便会失效,在分散性方面便与其它算法没有区别.
综上所述,随着优化问题复杂度的增加,改进算法在收敛性、分散性及运算复杂度的优势会逐渐增加,但在解决复杂度较低的优化问题时,算法的优势会减弱甚至成为弱势.因而在实际生产中,当焊接机器人的焊点较多时,采用DTC-MOPSO算法会有比较明显的优化效果.
5 结论本文研究了焊接机器人多目标路径规划问题.在优化问题中,对多目标粒子群算法TC-MOPSO进行了改进以适用于离散多目标优化问题,形成了可以求解离散多目标优化问题的DTC-MOPSO算法.通过对100个点的多目标路径规划的求解,并与两种经典的多目标优化算法相比较,结果证明改进的算法大大提高了算法的收敛性和解的分散性.在焊接机器人多目标路径规划问题中,以安川机器人ES165D的焊枪路径长度和能耗作为优化目标,用DTC-MOPSO算法求解出了多目标路径规划问题的非劣解,并与另外两种算法比较,结果显示新算法所得的非劣解在收敛性和分散性均要好于另外两种经典的优化算法,为焊接生产提供了一定的指导意义.同时,由两次优化对象的结果可以得出,改进算法在优化问题的复杂程度不同时,优势也不同.当优化问题较复杂时,运用DTC-MOPSO算法可以得到较好的效果; 而当优化问题复杂度降低时,DTC-MOPSO算法的效果优势会减弱.因此,本文方法在求解焊点较多的焊接机器人路径规划中有较好的优化效果.
| [1] | Wang X, Shi Y, Ding D, et al. Double global optimum genetic algorithm-particle swarm optimization-based welding robot path planning[J]. Engineering Optimization, 2015 . DOI:10.1080/0305215X.2015.1005084 |
| [2] | Chettibi T, Lehtihet H E. Minimum cost trajectory planning for industrial robots[J]. European Journal of Mechanics A/Solids, 2004 (23): 703–715. |
| [3] | 顾晨. 六自由度机械臂的动态路径规划和控制研究[D]. 镇江:江苏科技大学, 2014. Gu C. Research of dynamic path planning and control of Six degrees of freedom manipulator[D]. Zhenjiang:Jiangsu University of Science and Technology, 2014. |
| [4] | 盛巍. 基于多自由度工业机械臂的避障路径规划技术的研究[D]. 无锡:江南大学, 2012. Sheng W. The research of planning technology for obstacle avoidance path based on multi-degree of freedom industrial manipulator[D]. Wuxi:Jiangnan University, 2012. |
| [5] | Yang H, Shao H. Distortion-oriented welding path optimization based on elastic net method and genetic algorithm[J]. Journal of Materials Processing Technology, 2009, 209 (9): 4407–4412. DOI:10.1016/j.jmatprotec.2008.11.019 |
| [6] | Hu X, Eberhart R. Multiobjective optimization using dynamic neighborhood particle swarm optimization[C]//Proceedings of the 2002 Congress on Evolutionary Computation. Piscataway, NJ, USA:IEEE, 2002:1677-1681. |
| [7] | Janga Reddy M, Nagest Kumar D. An efficient multi-objective optimization algorithm based on swarm intelligent for engineering design[J]. Engineering Optimization, 2007, 39 (1): 49–68. DOI:10.1080/03052150600930493 |
| [8] | Li X. Better spread and convergence:Particle swarm multiobjective optimization using the maximin fitness function[C]//Genetic and Evolutionary Computation-GECCO 2004. Berlin, Germany:Springer, 2004:117-128. |
| [9] | Coello C, Pulido G T, Lechuga M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8 (3): 256–279. DOI:10.1109/TEVC.2004.826067 |
| [10] | Reddy M, Kumar J, Nagesh D. An efficient multi-objective optimization algorithm based on swarm intelligence for engineering design[J]. Engineering Optimization, 2007, 39 (1): 49–68. DOI:10.1080/03052150600930493 |
| [11] | 向长城, 黄席樾, 杨祖元, 等. 小生境粒子群优化算法[J]. 计算机工程与应用, 2007, 43 (15): 41–43. Xiang C C, Huang X Y, Yang Z Y, et al. Niche particle swarm optimization algorithm[J]. Computer Engineering and Applications, 2007, 43 (15): 41–43. |
| [12] | Mostaghim S, Teich J. Strategies for finding good local guides in multi-objective particle swarm optimization (MOPSO)[C]//Proceedings of the 2003 IEEE Swarm Intelligence Symposium. Piscataway, NJ, USA:IEEE, 2003:26-33. |
| [13] | 王学武, 薛立卡, 顾幸生. 三态协调搜索多目标粒子群优化算法[J]. 控制与决策, 2015 (11): 1945–1952W. |
| [14] | Chen S M, Chen C Y. Solving the traveling salesman problem based on the genetic simulated annealing ant colony system with particle swarm optimization techniques[J]. Expert Systems with Applications, 2011, 38 (12): 14439–14450. DOI:10.1016/j.eswa.2011.04.163 |
| [15] | Albayrak M, Allahverdi N. Development a new mutation operator to solve the traveling salesman problem by aid of genetic algorithms[J]. Expert Systems with Applications, 2011, 38 (3): 1313–1320. DOI:10.1016/j.eswa.2010.07.006 |
| [16] | 张海荣. 多关节机器人的运动轨迹规划研究[D]. 南京:南京工业大学, 2006. Zhang H R. Study of moving path planning of the manipulator[D]. Nanjing:Nanjing Tech University, 2006. |
| [17] | 刘亚军. 6R操作臂逆运动学分析与轨迹规划[J]. 机械工程学报, 2012, 48 (3): 9–15. Liu Y J. Inverse kinematics and trajectory planning of 6R serial manipulators[J]. Journal of Mechanical Engineering, 2012, 48 (3): 9–15. DOI:10.3901/JME.2012.03.009 |
| [18] | Kennedy J, Eberhart R C. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. Piscataway, NJ, USA:IEEE, 1995:1942-1948. |
| [19] | Kennedy J, Eberhart R C. A discrete binary version of the particle swarm algorithm[C]//Proceedings of the IEEE International Conference on Systems, Man and Cybernetics. Piscataway, NJ, USA:IEEE, 1997:4104-4108. |
| [20] | Parsopoulos K E, Vrahatis M N. Recent approaches to global optimization problems through particle swarm optimization[J]. Natural Computing, 2002, 1 (2/3): 235–306. DOI:10.1023/A:1016568309421 |
| [21] | Clerc M. Discrete particle swarm optimization, illustrated by the traveling salesman problem[M]. Berlin, Germany: Springer , 2004 : 219 -239. |
| [22] | Deb K, Pratap A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6 (2): 182–197. DOI:10.1109/4235.996017 |
| [23] | Luo L P, Yuan C, Yan R J, et al. Trajectory planning for energy minimization of industry robotic manipulators using the Lagrange interpolation method[J]. International Journal of Precision Engineering and Manufacturing, 2015, 16 (5): 911–917. DOI:10.1007/s12541-015-0119-9 |



