1 引言
柔性作业车间调度问题(flexible job-shop scheduling problem,FJSP)是对传统的作业车间调度问题的扩充,突破了机器唯一性的限制,增加了调度的灵活性,更加贴近生产现状.FJSP在考虑工件所有工序加工顺序的同时,还要考虑每道工序的机器分配问题.车间调度算法的本质是NP-hard问题,因此,本文研究的更复杂问题也是NP-hard问题[1-2].因此,对FJSP的研究具有重要的理论意义和应用价值.
目前,求解FJSP的方法有人工神经网络、进化计算、智能优化算法等,但是研究的热点主要集中在智能优化算法上,如粒子群优化算法(particle swarm optimization,PSO)、蚁群优化算法(ant colony optimization,ACO)、遗传算法(genetic algorithm,GA)等.Xi等[3]针对生产管理和组合优化的FJSP,采用混合粒子群优化算法来求解,引入了模拟退火算法来实现局部搜索,有效地避免了算法陷入局部最优; Na等[4]针对多层次工作结构的FJSP,建立了混合整数线性规划模型,为了提高GA计算实例的性能,提出一种优先规则和局部搜索规则的GA来求解; Imen等[5-6]针对最大完工时间最小化的FJSP,提出了一种新的GA来求解,这种新算法采用了新的染色体表示,并采用不同的交叉和变异策略,通过对基准实例和一个药品制造公司的具体数据的测试,表明了所提出算法的有效性; Mo等[7]针对以最大完工时间最小化和加工成本为目标的多目标FJSP,建立了一个新的非线性整数规划模型,为了权衡目标函数,提出一种基于ELECTRE方法的多目标GA; 白俊杰等[8]针对分批调度的多目标FJSP,提出一种粒子群优化算法来求解,为了避免决策者在非劣解中选择困难,加入决策者偏好信息来引导算法的搜索方向,并通过实例仿真验证了算法的有效性和可行性; 赵诗奎[9-10]针对最大完工时间最小化的FJSP,提出一种混合遗传算法来求解,为了增强粒子邻域搜索能力,在GA中引入2级邻域搜索策略,并通过基准算例验证了算法的有效性; 施进发等[11]针对传统作业车间调度问题的局限性,建立了以机器总负荷、成品合格率和设备利用率等为目标的FJSP模型,并利用蚁群算法来求解,为了提高算法求解效率和防止算法过程中非劣解的产生,优化设计了调度布局和采用连续空间的蚁群算法,并通过具体生产实例验证了算法的有效性; 石小秋等[12]针对传统柔性作业车间调度问题,提出一种离散多种群入侵杂草优化算法,引入了多种群思想,并采用自适应变异位数策略和邻城搜索策略来提高算法的收敛速度和寻优精度; Ka等[13]针对多目标FJSP,建立了以最大完工时最小化、关键机器工作量和总工作量三个性能指标的多目标FJSP模型,并提出了一种混合离散萤火虫算法来求解,为了平衡资源限制和机器灵活性,构建了一个合适的吸引力、距离和移动来实现连续函数到离散函数的转换,并通过对基准函数进行测试验证了算法的有效性.
蝙蝠算法[14](bat algorithm,BA)是由学者Yang于2010年提出的一种新的元启发式搜索算法,它的机理是模拟蝙蝠的回声定位原理.蝙蝠在搜寻猎物的过程中,通过调整超声波脉冲强度来实现大范围的搜索.在飞行的过程中,蝙蝠通过不断地调整超声波脉冲频率来掌握猎物不断变化的位置.自从BA提出以来,该算法已经逐渐在不同领域受到学者的重视.Ali[15]将BA应用到电力系统稳定性的研究中; 石浩等[16]将BA应用到WSN定位中去; 陈媛媛等[17-18]提出一种思维进化蝙蝠算,并将其应用到混合气体红外光谱特征选择中.除了实际的应用以外,还有许多学者将BA应用到函数优化[19]、模式识别[20]、工程问题优化[21]等.在车间调度领域,自从BA被提出以来,已经有很多学者对此进行研究.Marichelvam等[22-23]于2013年将BA应用到混合流水车间调度问题上,并通过仿真实验表明BA比遗传算法和粒子群算法在求解该问题上更有效; Luo等[24]于2014年提出一种离散BA求解置换流水车间调度问题,仿真实验结果表明了BA在求解车间调度问题上是有效的; Zhang等[25]于2014年提出一种改进BA求解置换流水车间调度问题,仿真实验结果表明改进后的BA具有较好的可行性和有效性; La等[26]于2015年针对两阶段混合流水车间调度问题,提出一种混合蝙蝠算法来求解,仿真实验结果表明该算法优化效果好于原BA算法.
从上述文献研究成果可以看出,BA已经应用到很多领域,但是应用到FJSP问题上的还很少,研究主要集中在混合流水车间调度和置换流水车间调度问题上.基于此,本文针对FJSP特点,提出了一种更加有效的改进蝙蝠算法对FJSP进行求解.为了有效地避免算法早熟收敛、提高蝙蝠算法的全局搜索能力和精度,本文对FJSP环境下的基本蝙蝠算法做如下改进:
(1) 在粒子编码阶段,为了有效、简洁地表达出所有工件的工序与粒子种群之间的关系,本文提出一种单层整数编码策略,并定义了FJSP的相关操作来完成种群的初始化工作;
(2) 在算法的速度和位置计算方面,算法重新定义了速度和位置的相关算子,使其适应于FJSP环境;
(3) 重新调整惯性权重的值,在粒子种群进化的过程中,合理地控制全局搜索能力和局部探索能力是非常重要的,为了克服基本BA的固定参数不足的缺点,本文采用呈指数递减的惯性权重策略.
2 问题描述及建模FJSP可以描述为: 设有n个待加工工件,用集合形式表示为J={J1,J2,…,Ji,…,Jn}(i∈[1,n]且i∈N*); m台待用机器,用集合形式表示为M={M1,M2,…,Mj,…,Mm}(j∈[1,m]且j∈N*); 每个工件需要经过若干道工序加工才能完成,但是每个工件的工序数量不一定相同,且每道工序可以选择在给定的不同机器设备上进行加工; λ表示总工序数; λi表示第i个工件的工序数量; Sij表示第i个工件的第j道工序上可选择加工的机器数量; Oij表示第i个工件的第j道工序; Wijk表示第i个工件的第j道工序在机器k上加工; Mij表示第i个工件的第j道工序的可加工机器的集合; Tijk表示第i个工件的第j道工序在机器k上加工时间.本文研究的FJSP调度的目标需要满足以下的约束条件,并需要确定工件的加工顺序和各个工序所选择的加工设备,最终使得调度性能指标达到最优.满足的约束条件有:
(1) 每道工序可选择的机器可以有多台,但是只能从可选机器集中选择一台进行加工.
(2) 每道工序一旦开始加工,在加工过程中不能中断.
(3) 一台机器在同一时刻最多只能有一个工件在上面加工.
(4) 工件的到达时间包含在加工时间内.
(5) 已经加工完成的机器在工件没有运送到达时可以选择停止或空载运行.
FJSP的调度目标是找出n个工件所有工序的一个加工顺序,使其总完工时间到达最小.计算工件所有工序总完工时间的计算方法为
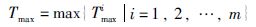
|
(1) |
式(1)中,Tmaxi表示机器i上的最后一个工件的完成时间; Tmax表示所有工件都完工的最后时刻的完工时间,即总调度时间.
3 改进蝙蝠算法 3.1 编码策略改进蝙蝠算法求解FJSP问题首先要解决的就是编码问题,编码方案是蝙蝠算法和FJSP之间的一座桥梁.为此,编码方案需要做到以下3点:
(1) 能够表示每个工件工序之间的先后顺序;
(2) 能够表示每个工件工序所要选择的加工机器;
(3) 表达方式要尽量简洁.为了达到这3点,本文采用单层整数编码策略(single integer encoding strategy,SIES),其编码大小为λ.编码形式表示为O=m1,m2,…,mp,…,mλ,其中,mp代表的含义是对应工件的工序所选择的加工机器且mp∈[1,m].首先,编码策略O给出了所有工序的顺序,即m1,m2,…,mp,…,mλ; 其次,编码策略O给出了每道工序所选择的加工机器mp; 最后,编码策略O的表达方式比较简洁.下面给出编码策略的具体示例.
表 1所示为一个3×4的FJSP实例,符号“-”表示对应工序不能在该机器上加工.
| 工件 | 工序 | 可选机器和对应加工时间 | |||
| M1 | M2 | M3 | M4 | ||
| J1 | O11 | 3 | - | 4 | 2 |
| O12 | 3 | - | 3 | 3 | |
| O13 | - | 5 | 3 | 1 | |
| J2 | O21 | 4 | 2 | 3 | 5 |
| O22 | 4 | 4 | - | 3 | |
| O31 | 2 | 4 | 3 | - | |
| J3 | O32 | 1 | - | 3 | 2 |
| O33 | 2 | 2 | - | 5 | |
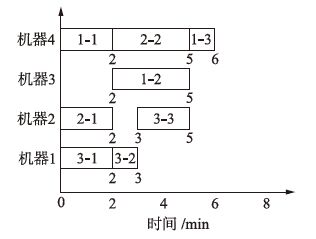
对应的单层整数编码策略如图 1所示,工序编码序列为O=4,3,4,2,4,1,1,2,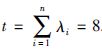

|
| 图 1 单层整数编码图 Figure 1 Chart of single integer encoding |
种群初始化是算法的初期工作,为了完成蝙蝠算法求解FJSP的种群初始化工作,需要完成算法与调度之间的相关链接定义,如定义1所示.
定义1 种群初始化相关操作定义
工序最大选择机器矩阵PSM(the process maximum selection machine matrix,PSM): 表达了每道工序所能选择的加工机器集合.以表 1中的实例数据为例,可得

|
PSM是一个λ×max(Sij)矩阵,其中max(Sij)表示所有工序中能选择的机器的最大个数,∞表示该工序不在该机器上进行加工.例如,第1行(1,3,4,∞)表示O11可在机器1、3、4上进行加工,以此类推.
工序选择机器数矩阵PSMN(the process selection machine number matrix,PSMN): 表达了每道工序所能选择的加工机器数量.以表 1中的实例数据为例可得,PSMN是一个λ×2矩阵.例如,第1行(1,3)表示O11可加工的机器数量为3,以此类推.
下面给出种群初始化工作的算法伪代码.
定义变量:
工序最大选择机器矩阵: PSM
工序选择机器数矩阵: PSMN
位置: X
种群规模: PopSize
工序数量: λ
begin:
for i=1 to PopSize do
begin:
for j=1 to λ do
begin:
X(i,j)=PSM(j,rand i[1 PSMN(j,2)],
1,1)
end
end
end
3.3 位置更新假设搜索空间为D维,vi(t)和xi(t)分别表示t时刻蝙蝠i的速度位置,则t+1时刻蝙蝠i的速度vi(t+1)和位置xi(t+1)更新公式:
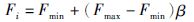
|
(2) |
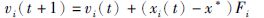
|
(3) |
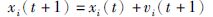
|
(4) |
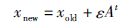
|
(5) |
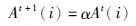
|
(6) |
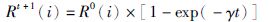
|
(7) |
式(2)~式(7)中,Fi表示蝙蝠i的更新频率,Fmax和Fmin分别表示更新频率的最大值和最小值.β是随机产生的数且β∈[0,1]; x*表示全局最优解,xold表示的是一个从最优解集中随机选择的一个最优解,At表示响度平均值,A(i)表示脉冲的响度,ε是随机产生的数且ε∈[-1,1],R(i)表示发射速率,0<α<1,γ>0,α∈R,γ∈R.
标准的蝙蝠算法流程如文[14]所示.BA的首次提出主要是解决连续域函数优化问题.为了将其应用到离散域优化问题,Yang[26]等提出一种二进制蝙蝠算法(binary bat algorithm,BBA).FJSP虽然是离散域组合优化问题,但是无法直接将BBA应用到FJSP中.因此,根据FJSP的特点,本文直接将BA中连续量在求解离散域上圆整化,且式(4)需要重新定义,如式(8)所示:
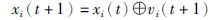
|
(8) |
式(8)中,是加法算子,含义是利用速度vi(t+1)与位置xi(t)的变换来实现算法在可行解空间的移动.这里的变换涉及到置换序列和变异序列的定义,其中置换序列的定义为: 位置为X,置换序列(i,j)的操作为交换X中第i个元素和第j个元素; 变异序列的定义为: 每经过一次迭代,如果当前最好解劣于种群最好解,则进行变异.变异序列(i,j)的操作是指将Oij的选择进行变异且变异的值属于Mij.
3.4 惯性权重调整蝙蝠算法中速度与位置的更新过程和粒子群优化算法[8]有一定的相似性.在式(9)[9]中,惯性权重w的引入,平衡了算法的全局和局部搜索能力.为了使算法在种群初期拥有比较全面搜索的能力,采用呈指数递减的方式来计算公式,如式(10)所示:
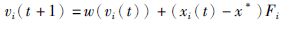
|
(9) |
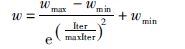
|
(10) |
式中,wmax和wmin分别是惯性权重的最大值和最小值,iter是当前的迭代次数,MaxIter是最大迭代次数.
3.5 算法流程综上所述,下面给出求解FJSP的改进蝙蝠算法的基本步骤:
步骤1 参数初始化,主要包括蝙蝠种群大小PopSize、脉冲响度A(i)和频率F(i)、脉冲发射速率R(i)、惯性权重最大值wmax和最小值wmin、工件数量n、机器数量m等.
步骤2 基于单层整数编码策略产生编码序列并初始化种群.
步骤3 计算适应度值.
步骤3.1 将n个工件载入加工矩阵和临时资源池中.
步骤3.2 在加工矩阵中从每个工件的第1道工序开始加工,首先判断该工序所需要的机器是否被其它工序所占用,如果不是,则该工件标记为可加工状态,同时记录对应的工件号和工序号,否则标记该工件为等待加工状态.
步骤3.3 在加工矩阵和临时资源池中,从第1个工件开始加工,先判断工件是否处于正在被加工状态,如果是且剩余时间大于0,则该工件继续加工; 如果否,再判断该工件的所有工序是否都已经完成: 如果是则释放该工件所占用的机器; 否则,将该工件的下一道工序载入加工矩阵和临时资源池中.
步骤3.4 判断所有工件是否都已经完成,如果是则转步骤3.5,否则转步骤3.2.
步骤3.5 输出适应度值.
步骤4 判断是否达到终止条件.如果是,转步骤3; 否则转步骤5.
步骤5 通过式(2)、式(8)、式(9)调整频率和更新速度和位置产生新解xnew.
步骤6 如果rand>ri成立,从最好解集中选择一个,通过式(5)产生解,并覆盖原来的解,得到新解xnew.
步骤7 计算xnew对应的适应度值fitnew.
步骤8 判断fitnew<fit(i)和rand<Ai是否同时成立,如果是,则接受新解,并利用式(6)、式(7)更新ri和Ai.否则进行越界判断,并根据式(8)进行更新.
步骤9 转步骤4.
步骤10 输出最佳解.
说明 加工矩阵存储的是工件与工序的相关信息,包括未被激活、等待加工、正在加工和已经完成加工等信息.临时资源池中存储的是机器的2种状态: 0,不可用态; 1,可用态.
4 实例仿真与分析本文改进蝙蝠算法求解FJSP采用Matlab编程环境实现,在处理器为Pentium 1.6 GHz,内存为8 GB的PC机下运行.算法参数设置如表 2所示.
| 参数名称 | 值 |
| PopSize | 100 |
| MaxIter | 500 |
| Fmax | 1 |
| Fmin | 0 |
| α | 0.9 |
| γ | 0.9 |
| A | 0.25 |
| wmax | 0.96 |
| wmin | 0.36 |
这里,上述参数的设置值是根据每个实例的50次实验得到的,下面做详细的说明: PopSize为种群规模,在实验中,使用了PopSize=10,15,20,50,100,150,250,从实验中发现PopSize取100时对于每个实例的优化问题效果良好,因此在实验中PopSize使用固定值100; MaxIter为最大迭代次数,在实验中发现算法在迭代次数250左右开始收敛到最好解,因此这里设置MaxIter为500; Fmax和Fmin分别为频率的最大值和最小值,α和γ为常量,A为响度,其中α类似于模拟退火算法中的冷却因素,这里它们分别设置为1、0、0.9、0.9和0.25,这里的设置是依据参考文[14]中的实验设置; w为惯性权重,wmax和wmin分别为惯性权重的最大值和最小值,较大的w有利于算法的全局搜索,较小的w有利于算法的局部搜索,但是过小的w会使得群体失去探索的性能,根据表 5中的实验结果,wmin设置为0.36,wmax设置为0.96.
4.1 实例测试为了比较验证本算法的性能,采用文[27-29]中的3个实例进行测试,并与文献中所提出的算法对应的实例的计算结果进行比较.
实例1 数据来源于文[27]中的数据,分别有10个工件和6台机器.利用本文提出的改进蝙蝠算法对实例进行优化求解,对实例独立计算50次,得到的最优解为82,对应最优解的甘特图如图 3所示.

|
| 图 3 实例1最优解的甘特图 Figure 3 The Gantt chart of the optimal solution for instance 1 |
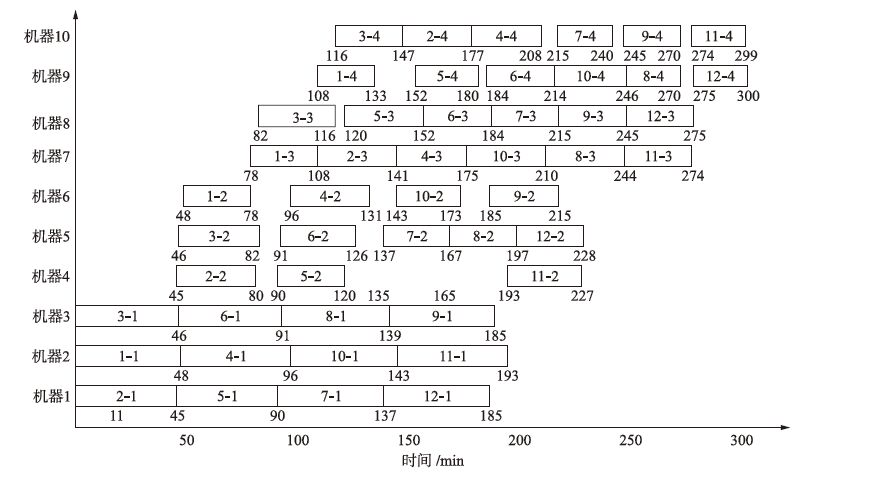
实例2 数据来源于文[28]中的数据,共有12炉钢水(即工件),在加工过程中,经过的4道工序分别为炼钢、精炼、连铸和轧制,其中,每道工序的并行机器数分别为3、3、2和2.文[6]中采用遗传算法求解得到的最优解为347,文[28]采用粒子群算法求解得到的最优解为317.利用本文提出的改进蝙蝠算法对实例进行优化求解,对实例独立计算50次,得到的最优解为300,对应最优解的甘特图如图 4所示.
|
| 图 4 实例2最优解的甘特图 Figure 4 The Gantt chart of the optimal solution for instance 2 |
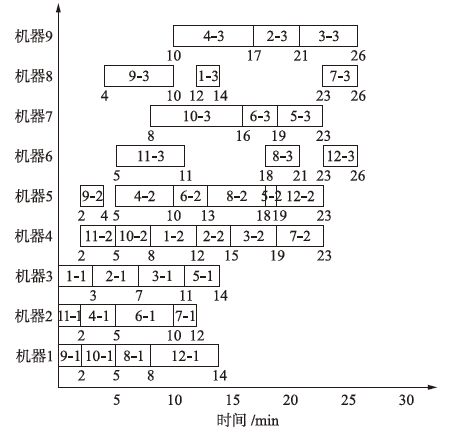
实例3 数据来源于文[29]中的数据,有12个工件、9台机器和3道工序,每道工序中并行机器数分别为3、2和4.利用本文提出的改进蝙蝠算法对实例进行优化求解,对实例独立计算50次,得到的全局最优解为26,对应最优解的甘特图如图 5所示.
|
| 图 5 实例3最优解的甘特图 Figure 5 The Gantt chart of the optimal solution for instance 3 |
将本文提出的改进蝙蝠算法与其它几种使用相同数据,并且具有代表性的算法进行结果对比,比较结果如表 3所示,其中,符号“-”表示对应文献中的算法未对该实例进行求解.
| 实例 | 文献算法 | 文献结果 | 本文结果 |
| 实例1 | NSGA-II | 85 | 82 |
| 实例2 | GA/PSO | 347/317 | 300 |
| 实例3 | GSA | 28 | 26 |
表 3给出了实验对比结果,文[27]算法使用基于改进非支配排序遗传算法对实例1进行求解,得到的最好解为85,本文算法得到的最好解为82,最好解精度比算例1中的算法提高了3.529%; 文[6]算法使用遗传算法、文[28]使用混合粒子群算法对实例2进行求解,得到的最好解分别为347和317,本文算法得到的最好解为300,最好解精度比实例2中的算法分别提高了5.363%和13.545%; 文[29]算法使用改进的遗传模拟退火算法对实例3进行求解,得到的最好解为28,本文算法得到的最好解为26,最好解精度比算例3中的算法提高了7.143%.在上述3个实例中,遗传算法、粒子群算法和模拟退火算法都存在早熟、易陷入局部最优等缺点.在蝙蝠算法中,惯性权重w的引入,平衡了粒子的全局搜索和局部探索的能力.为了使粒子在初期能进行较全面的搜索,引入了呈指数递减的惯性权重方式,有效地避免了粒子早熟收敛.从上述比较结果可以得知,本文的改进蝙蝠算法在求解FJSP上是有效的,并且能够取得良好的结果.
表 4给出了50次实验下本文算法求解3个实例的性能分析.在表 4中,给出本文算法求解3个实例的平均计算时间和收敛到最好解的平均迭代次数,对于算法求解实例1,在平均迭代次数233时算法收敛于最好解82,平均计算时间为15 s; 对于算法求解实例2,在平均迭代次数326时算法收敛于最好解300,平均计算时间为32 s; 对于算法求解实例3,在平均迭代次数162时收敛于最好解162,平均计算时间为11 s.可以看出,本文算法在求解FJSP上能在较短的时间内获得较好的解,且具有较快的收敛性能.
| 实例 | 最好解/
最大解 | 平均计算
时间/s | 达到最好解
的百分比 | 收敛到最好解的
平均迭代次数 |
| 实例1 | 82/86 | 15 | 92 | 233 |
| 实例2 | 300/317 | 32 | 84 | 326 |
| 实例3 | 26/27 | 11 | 96 | 162 |
表 5给出了本文算法中惯性权重w在10个不同数值下的实验结果对比,较大的w有利于算法的全局搜索能力,较小的w有利于增强算法的局部探索能力,但是w取值过小时,算法收敛速度过快,易导致算法早熟收敛.从表 5中可以得到,当wmin=0.36,wmax=0.96时,对3组实例测试取得的效果最佳; 当wmin=0.26,wmax=0.96和wmin=0.46,wmax=0.96时,对实例1和实例3在最好解上取得的效果也最佳; 当wmin=0.16,wmax=0.96和wmin=0,wmax=1时,对3个实例在最好解上取得的效果并不是最佳,原因是过小的惯性权重易导致算法早熟收敛;当wmin=0.16,wmax=0.56、wmin=0.26,wmax=0.56、wmin=0.36,wmax=0.56和wmin=0.46,wmax=0.56时,对3个实例在最好解和达到最好解的百分比上取得的效果并不是最佳,原因是初始的w较小,算法前期无法进行充分的全局搜索,导致算法在可行解空间搜索具有局限性.因此,本文建议在改进蝙蝠算法求解FJSP上,将wmin的值设置为0.36,wmax的值设置为0.96.
| 参数设置 | 实例1/实例2/实例3 | |||
| 最好解 | 最大解 | 达到最好解的百分比 | 平均解 | |
| w=1 | 85/305/28 | 90/325/31 | 82/80/84 | 85.54/307.10/28.32 |
| wmin=0,wmax=1 | 87/313/28 | 95/337/32 | 76/74/78 | 87.94/315.12/28.56 |
| wmin=0.16,wmax=0.56 | 86/310/28 | 92/335/32 | 78/74/80 | 86.74/312.96/28.50 |
| wmin=0.16,wmax=0.96 | 83/307/27 | 89/320/30 | 82/80/90 | 83.66/307.98/27.20 |
| wmin=0.26,wmax=0.56 | 86/308/28 | 92/329/31 | 80/74/82 | 86.58/310.08/28.34 |
| wmin=0.26,wmax=0.96 | 82/303/26 | 87/317/28 | 88/84/96 | 82.38/304.58/26.06 |
| wmin=0.36,wmax=0.56 | 85/307/27 | 92/327/31 | 80/76/82 | 85.72/308.16/27.42 |
| wmin=0.36,wmax=0.96 | 82/300/26 | 86/317/27 | 92/84/96 | 82.16/302.50/26.04 |
| wmin=0.46,wmax=0.56 | 83/306/27 | 90/325/30 | 84/80/88 | 83.68/307.96/27.22 |
| wmin=0.46,wmax=0.96 | 82/303/26 | 87/317/29 | 90/82/96 | 82.32/304.80/26.10 |
针对FJSP,本文提出了一种改进蝙蝠算法来求解.成功将蝙蝠算法应用到FJSP中的前提是要建立工序与粒子种群之间的关系,为此,提出一种单层整数编码策略方案; 其次,算法重新定义了粒子的速度和位置相关的算子.为了有效地避免算法早熟收敛、提高算法的全局搜索能力和精度,提出一种呈指数递减的惯性权重策略.最后,针对实际生产车间调度问题,建立了调度模型,设计了具体算法,实验结果表明改进蝙蝠算法在求解FJSP上的可行性和有效性,从而为解决这类问题提供了新的途径和方法.将算法应用于求解多目标FJSP以及调度规则的挖掘是进一步的研究方向.
| [1] | Garey E L, Johnson D S, Sethi R. The complexity of flowshop and job-shop scheduling[J]. Mathematics of Operations, 1976 (1): 117–129. |
| [2] | Rock H. The three-machine no-wait flow shop problem is NP-complete[J]. Association for Computing Machinery, 1984, 31 (2): 336–345. DOI:10.1145/62.65 |
| [3] | Xi W J, Wu Z M. An effective hybrid optimization approach for multi-objective flexible job-shop scheduling problems[J]. Computers and Industrial Engineering, 2005, 48 (2): 409–425. DOI:10.1016/j.cie.2005.01.018 |
| [4] | Na H, Park J. Multi-level job scheduling in a flexible job shop environment[J]. International Journal of Production Research, 2013, 52 (13): 3877–3887. |
| [5] | Imen D, Kinza N M, Assia L. A new genetic algorithm for flexible job-shop scheduling problems[J]. Journal of Mechanical Science and Technology, 2015, 29 (3): 1273–1281. DOI:10.1007/s12206-015-0242-7 |
| [6] | 崔建双, 李铁克, 张文新. 混合流水车间调度模型及其遗传算法[J]. 北京科技大学学报, 2005, 27 (5): 623–626. Cui J S, Li T K, Zhang W X. Hybrid flowshop scheduling model and its genetic algorithm[J]. Journal of University of Science and Technology Beijing, 2005, 27 (5): 623–626. |
| [7] | Mohamad R, Amirsaman K, Parviz F, et al. A hybrid multi-objective genetic algorithm based on the ELECTRE method for a capacitated flexible job shop scheduling problem[J]. The International Journal of Advanced Manufacturing Technology, 2015, 77 (1/2/3/4): 51–66. |
| [8] | 白俊杰, 龚毅光, 王宁生, 等. 多目标柔性作业车间分批优化调度[J]. 计算机集成制造系统, 2010, 16 (2): 396–403. Bai J J, Gong Y G, Wang N S, et al. Multi-objective flexible job shop scheduling with Lot-splitting[J]. Computer Integrated Manufacturing Systems, 2010, 16 (2): 396–403. |
| [9] | 赵诗奎. 求解柔性作业车间调度问题的两级领域搜索混合算法[J]. 机械工程学报, 2015, 51 (14): 174–184. Zhao S K. Bilevel Neighborhood Search hybrid algorithm for the flexible job shop scheduling problem[J]. Journal of mechanical engineering, 2015, 51 (14): 174–184. |
| [10] | Wang X J, Gao L, Zhang C Y, et al. A multi-objective genetic algorithm based on immune and entropy principle for flexible job-shop scheduling problem[J]. International Journal of Advanced Manufacturing Technology, 2010, 51 (5//6/7/8): 757–767. |
| [11] | 施进发, 焦合军, 陈涛. 交货期惩罚下柔性调度多目标Pareto优化研究[J]. 机械工程学报, 2012, 48 (12): 184–192. Shi J F, Jiao H J, Chen T. Multi-objective pareto optimization on flexible job-shop scheduling problem about due punishment[J]. Journal of Mechanical Engineering, 2012, 48 (12): 184–192. DOI:10.3901/JME.2012.12.184 |
| [12] | 石小秋, 石宇强, 袁雪娇. 离散多种群入侵杂草优化算法求解柔性作业车间调度算法[J]. 信息与控制, 2015, 44 (2): 238–243. Shi X Q, Shi Y Q, Yuan X J. Invasive weed optimization algorithm with discrete nulti-popalation for the flexible job-shop scheduling problem[J]. Information and Control, 2015, 44 (2): 238–243. |
| [13] | Karthikeyan S, Asokan P, Nickolas S. A hybrid discrete firefly algorithm for multi-objective flexible job shop scheduling problem with limited resource constraints[J]. The International Journal of Advanced Manufacturing Technology, 2014, 72 (9/10/10/12): 1567–1579. |
| [14] | Yang X S. A new metaheuristic bat-inspired algorithm[J]. Nature Inspired Cooperative Strategies for Optimization, 2010, 284 : 65–74. DOI:10.1007/978-3-642-12538-6 |
| [15] | Ali E S. Optimization of power system stabilizers using bat search algorithm[J]. International Journal of Electrical Power and Energy Systems, 2014, 61 : 683–690. DOI:10.1016/j.ijepes.2014.04.007 |
| [16] | 石浩, 王万良, 李燕君, 等. 基于Lévy飞行特征的蝙蝠算法及其在WSN定位中的应用[J]. 传感技术学报, 2015, 28 (6): 888–894. Shi H, Wang W L, Li Y J, et al. Bat algorithm based on Lévy flight feature and its localization application in WSN[J]. Chinese Journal of Sensors and Actuators, 2015, 28 (6): 888–894. |
| [17] | 陈媛媛, 王志斌, 王召巴. 基于改进蝙蝠算法的红外光谱特征选择[J]. 红外与激光工程, 2014, 43 (8): 2715–2721. Chen Y Y, Wang Z B, Wang Z B. Feature selection of infrared spectrum based on improved bat algorithm[J]. Infrared and Laser Engineering, 2014, 43 (8): 2715–2721. |
| [18] | 陈媛媛, 王志斌, 王召巴. 思维进化蝙蝠算法及其在混合气体红外光谱特征选择中的应用[J]. 红外与激光工程, 2015, 44 (3): 845–851. Chen Y Y, Wang Z B, Wang Z B. Mind evolutionary bat algorithm and its application to feature selection of mixed gases infrared spectrum[J]. Infrared and Laser Engineering, 2015, 44 (3): 845–851. |
| [19] | Yang X S. Bat algorithm for multi-objective optimization[J]. International Journal of Bio-Inspired Computation, 2011, 3 (5): 267–274. DOI:10.1504/IJBIC.2011.042259 |
| [20] | Komarasamy G, Wahi A. An optimized k-means clusterin-g technique using bat algorithm[J]. European Journal of Scientific Research, 2012, 84 (2): 263–273. |
| [21] | Yang X S, Gandomi A H. Bat algorithm:A novel approach for global engineering optimization[J]. Engineering Com-putation, 2012, 29 (5): 267–289. |
| [22] | Marichelvam M K, Prabaharan T. A bat algorithm for realistic hybrid flowshop scheduling problems to minimize makespan and mean flow time[J]. ICTACT Journal on Soft Computing, 2012, 3 (1): 428–433. DOI:10.21917/ijsc |
| [23] | Marichelvam M K, Prabaharan T, Yang X S, et al. Solving hybrid flow shop scheduling problems using bat algorithm[J]. International Journal of Logistics Economics and Globalisation, 2013, 5 (1): 15–29. DOI:10.1504/IJLEG.2013.054428 |
| [24] | Luo Q F, Zhou Y Q, Xie J, et al. Discrete bat algorithm for optimal problem of permutation flow shop scheduling[J]. Scientific World Journal, 2014, 2014 : 1–15. |
| [25] | Zhang J J, Li Y G. An improved bat algorithm and its application in permutation flow shop scheduling problem[J]. Advanced Materials Research, 2014, 1049-1050 : 1359–1362. DOI:10.4028/www.scientific.net/AMR.1049-1050 |
| [26] | Dekhici L, Belkadi K. A bat algorithm with generalized walk for the two-stage hybrid flow shop problem[J]. International Journal of Decision Support System Technology (IJDSST), 2015, 7 (3): 1–16. DOI:10.4018/IJDSST |
| [27] | 张超勇, 董星, 王晓娟, 等. 基于改进非支配排序遗传算法的多目标柔性作业车间调度[J]. 机械工程学报, 2010, 46 (11): 156–164. Zhang C Y, Dong X, Wang X J, et al. Improved NSGA-Ⅱ for the multi-objective flexible job-shop scheduling problem[J]. Journal of Mechanical Engineering, 2010, 46 (11): 156–164. DOI:10.3901/JME.2010.11.156 |
| [28] | 张其亮, 陈永生. 基于混合粒子群-NEH算法求解无等待柔性流水车间调度问题[J]. 系统工程理论与实践, 2014, 34 (3): 802–809. Zhang Q L, Chen Y S. Hybrid PSO-NEH algorithm for solving no-wait flexible flow shop scheduling problem[J]. Systems Engineering-Theory & Practice, 2014, 34 (3): 802–809. |
| [29] | Min D, Dunbing T, Adriana G, et al. Energy-efficient scheduling for a flexible flow shop using an improved genetic-simulated annealing algorithm[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29 (5): 418–429. DOI:10.1016/j.rcim.2013.04.001 |