2. 西南交通大学数学学院, 四川 成都 610031;
3. 西南交通大学交通运输与物流学院, 四川 成都 610031
2. School of Mathematics, Southwest Jiaotong University, Chengdu 610031, China;
3. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China
1 引言
多智能体系统是由多个交互通讯、协调合作的智能体组成的系统,目的在于解决大型、复杂的现实问题[1-2].近年来,随着应用的需要和技术的发展,多智能体系统在无人机编队飞行、机器人探测、传感器网络和集聚控制等领域得到了广泛应用,吸引了大量研究者的关注[3-4].一致性问题作为多智能体协调控制的基础,如今已成为控制学界的一个研究热点.
在实际的多智能体系统中,通讯网络带宽和智能体自身能量都是有限的.在这种情况下,控制设计的关键就在于能否充分利用有限的资源来保证系统的控制性能[5].众所周知,采用传统的采样控制,即周期采样控制方式[6],可以减少智能体之间的通信次数,从而节省计算资源.从系统分析和设计的角度看,周期采样方式易于接受.但从网络资源利用的角度看,当两个连续采样数据间仅存在微小变化、大小几乎相同时,若还是周期地执行控制任务,就会造成不必要的资源浪费[5, 7].为了克服周期采样控制方式的不足,文[8-9]提出了一种新的基于事件触发控制(event-triggered control)方法.所谓事件触发控制方法是在保证闭环系统具有一定性能(如稳定性)的情况下,一旦预先设定好的事件触发条件不成立,控制任务随即被执行.换句话说,事件触发控制就是控制任务“按需”执行,同时保证系统具有一定的性能[7, 10].目前,基于事件触发控制的多智能体系统一致性问题的研究已取得不少成果[11-23].如,文[11-14]主要研究的是基于事件触发控制的1阶多智能体系统的一致性问题; 文[15-16]基于事件触发控制研究了2阶多智能体系统的一致性问题; 文[17-21]分别针对一般线性和非线性多智能体系统的一致性问题进行了研究,其中文[17, 20]对系统具有时变时滞的情形给出了具体分析,文[18-19]讨论了系统在切换拓扑下的一致性问题; 文[22-23]主要研究了基于事件触发控制的领导跟随系统的一致性问题.多智能体系统的平均一致性问题作为一类重要的一致性问题,也已受到许多学者的关注和研究[11-13, 18, 21].
受已有成果的启发,本文研究的是基于事件触发控制的2阶多智能体系统的平均一致性问题.基于同步式触发机制给出了系统的一致性协议,通过对各智能体的状态进行分解将系统的一致性分析转化为稳定性证明,并利用矩阵理论和李亚普诺夫稳定性理论给出了系统达到平均一致性的充分条件.
2 问题描述 2.1 代数图论多智能体系统中智能体之间的通讯拓扑通常用结构图来描述.记G=(V,ε,A)为含有n个智能体的系统的通讯拓扑图,其中V={1,2,…,n}表示节点集合,ε⊆V×V表示边集合,A=(aij)∈Rn×n表示邻接矩阵.有向图中的一条边eij∈ε代表一个有序节点对(i,j),其中i为起始节点,j为目标节点,表示节点i可以接收到节点j的信息.在无向图中,任何节点之间的边都是无向的,如果节点i和节点j之间有边相连,则表示这两个节点可以相互传递信息,即有(i,j)∈ε⇔(j,i)∈ε.邻接矩阵A中的元素与边相关,aij=1eij∈ε且令aii=0.对于节点i,定义其邻居节点集为Ni={j∈V(i,j)∈ε,j≠i},入度为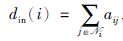
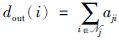
引理1 [3] 图G的拉普拉斯矩阵L具有以下性质:
(1) 0是矩阵L的一个特征值,1是其对应的特征向量,满足L1=0;
(2) 如果图G是有向强连通或无向连通的,那么0是矩阵L的单一特征值;
(3) 如果图G是有向强连通且平衡或无向连通的,那么矩阵L是对称半正定阵且有n个非负实数特征值,可按升序排列为
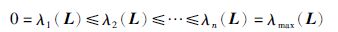
|
其中,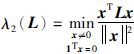
引理2 [15](Schur补) 对于对称矩阵S=ST,以下3个条件等价:
(1) S>0;
(2) S11>0,S22-S12TS11-1S12>0;
(3) S22>0,S11-S12S22-1S12T>0.
其中,S11、S22均为方阵.
引理3 [22] 若矩阵Am×m和Bm×m均为Hermitian阵,则如下不等式成立:
(1) λmin(A)+λmin(B)≤λmin(A+B);
(2) λmax(A)+λmax(B)≥λmax(A+B).
2.2 2阶多智能体系统的平均一致性考虑一个含有n个智能体的系统,对于每个智能体i,其2阶动力学方程描述为
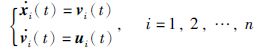
|
(1) |
其中,xi(t)∈Rm,vi(t)∈Rm和ui(t)∈Rm分别表示智能体i在t时刻的位置、速度和控制输入(也即一致性协议).
定义1 对于所有的智能体i∈V,如果存在控制协议ui(t)使得闭环系统在任何初始状态下满足:
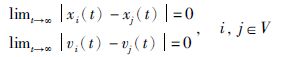
|
则称系统(1)达到一致.特别地,如果:
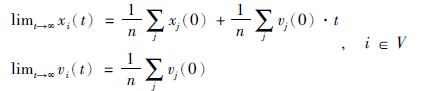
|
则称系统(1)达到平均一致.
3 主要结果 3.1 一致性协议本节考虑多智能体系统(1)在固定无向拓扑下的平均一致性问题.给出如下一致性协议:
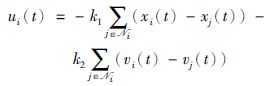
|
(2) |
其中,k1,k2>0分别为位置和速度反馈增益.
在基于同步式事件触发机制的一致性算法中,针对所有的智能体i∈V,设计触发函数f(具体形式将在后面给出),并根据触发函数对所有的智能体定义一个单调递增的时间点列tk(k=0,1,…),令i(t)=xi(tk),i(t)=vi(tk)(t∈[tk,tk+1))分别表示智能体i在此时间段内的采样位置和采样速度,其中tk称为触发时刻,数值上取为使得f=0的时间点值.因此,根据上述定义,可将式(2)改写成:
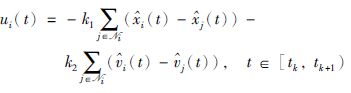
|
(3) |
式(3)即为基于事件触发控制的一致性协议.从式(3)中可以看出,智能体之间只有在事件触发时刻才进行信息通讯,在两个相邻事件触发时刻之间,控制输入保持不变,从而节省了网络和计算资源.
3.2 一致性分析本小节主要分析多智能体系统(1)在控制协议(3)的作用下平均一致性的收敛问题.
令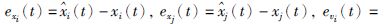
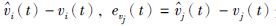
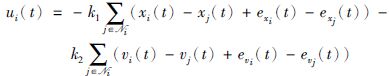
|
(4) |
于是整个闭环系统可以描述为
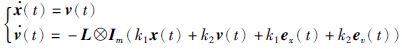
|
(5) |
其中,x=col(x1,x2,…,xn)∈Rn,v=col(v1,v2,…,vn)∈Rn,ex=col(ex1,ex2,…,exn)∈Rn,ev=col(ev1,ev2,…,evn)∈Rn分别为n个智能体的整体位置、速度、位置误差和速度误差.L是图G的拉普拉斯矩阵.
将位置和速度分解成如下形式:
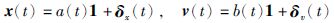
|
其中,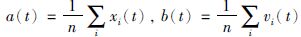
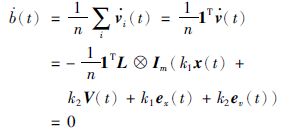
|
于是对于任意时间t,恒有:
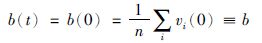
|
进而根据位置与速度的关系可得:
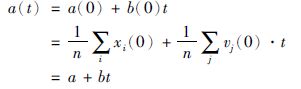
|
其中a、b为常数.从而有:
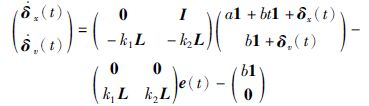
|
(6) |
其中,e(t)=col(ex(t),ev(t)),1是元素全为1的列向量且有1Tδx(t)=1Tδv(t)=0.
整理式(6)可得:
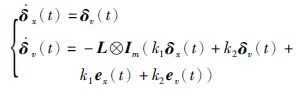
|
(7) |
于是,研究系统(1)的平均一致性问题在此转化为分析系统(7)的稳定性问题,下面将利用李亚普诺夫稳定性理论证明(7)是稳定的.
定理1 考虑多智能体系统(1)在一致性协议(3)的作用下,假设图G是无向连通的,若满足如下条件:
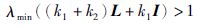
|
(8) |
且限定条件:
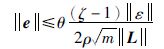
|
(9) |
成立,其中θ、ζ、ρ均为控制参数.则对于任意初始状态均有:
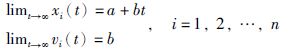
|
即系统能达到平均一致性.
证明 令ε(t)=col(δx(t),δv(t)),构造如下的李亚普诺夫函数:
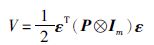
|
(10) |
其中,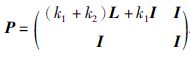
对式(10)求导得
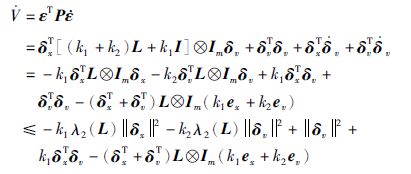
|
利用不等式性质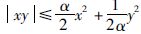
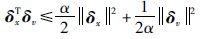
|
其中,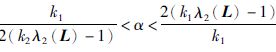
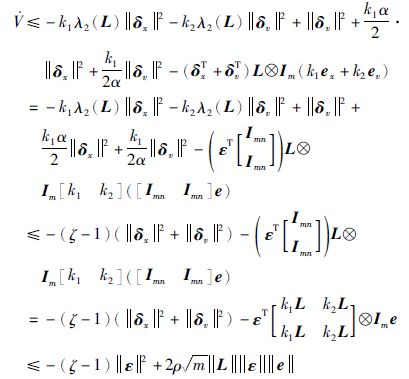
|
这里:
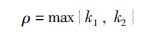
|
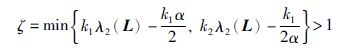
|
根据式(9),如果:
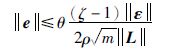
|
则有:
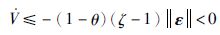
|
其中,0<θ<1.
于是,可将触发函数f定义为
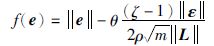
|
对于所有的智能体i∈V,其第k(k=0,1,…)个事件触发当且仅当f(e)=0.由状态误差的定义知,在tk时刻,e(t)=e(tk)=0,从而式(9)总是可满足的.
于是,由李亚普诺夫稳定性理论知,系统(7)是稳定的且对于任意的初始状态δx(0),δv(0),均有:
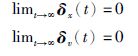
|
从而有:
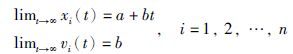
|
即系统(1)达到了平均一致性.
证毕.
为了表明在整个事件触发控制过程中不会产生Zeno现象,给出如下定理证明.
定理2 考虑多智能体系统(1)在一致性协议(3)的作用下,假设图G是无向连通的且满足式(8)和式(9),则对于所有的智能体i∈V,其任意2个连续事件触发时刻之间的间隔tk+1-tk不小于:
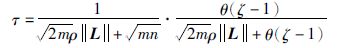
|
证明 类似于文[11],对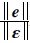
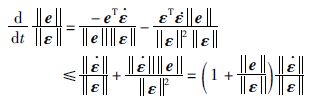
|
根据式(7),有:
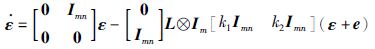
|
于是有:
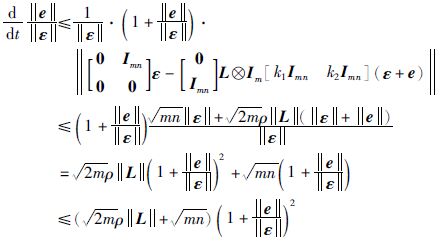
|
令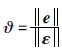
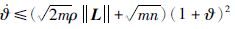
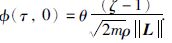
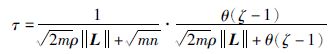
|
证毕.
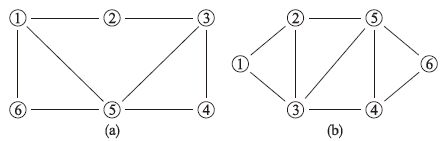
4 仿真实验本节用Matlab仿真实验来验证理论方案的有效性和正确性.为了能够更好地表明本文所给算法的合理性及本文的研究意义,实验中考虑一个由6个智能体组成的系统在2种不同拓扑结构(见图 1)下的一致性问题,并结合传统的周期采样控制算法和本文给出的事件触发控制算法分别进行实验.为了便于实验操作,仅考虑m=1的情况.
|
| 图 1 通讯拓扑图 Figure 1 Communication topology map |
在仿真实验中,多智能体的初始位置、速度和各参数分别设置为: x(0)=[4619.22.48],v(0)=[2.5-1.33.2-43-2.2],k1=1.5,k2=2,α=0.7,θ=0.99,周期采样T=0.15 s.
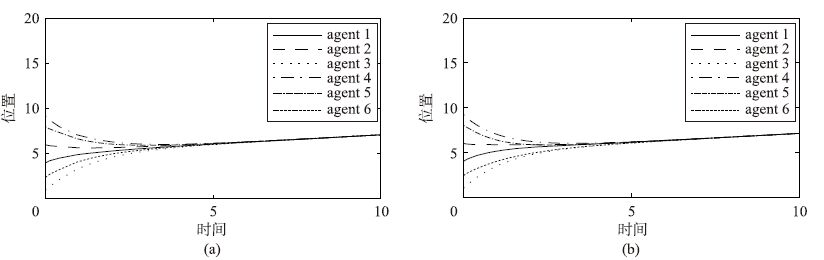
图 2和图 3分别给出了多智能体系统在2种不同拓扑结构下的位置和速度轨迹.
|
| 图 2 智能体的位置轨迹 Figure 2 Position tracking trajectories of the agents |
|
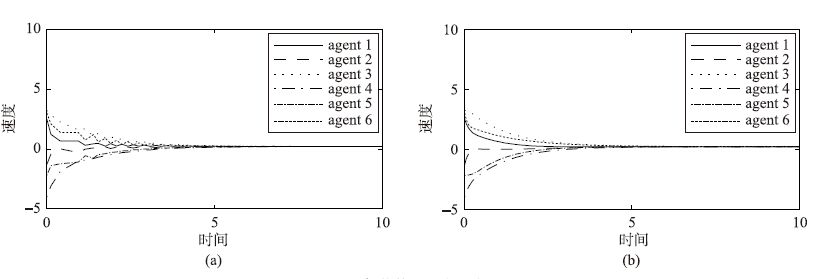
| 图 3 智能体的速度轨迹 Figure 3 Velocity tracking trajectories of the agents |
由图 2和图 3可知,在两种不同的拓扑结构下,系统中所有智能体的位置和速度状态最终在平均值处趋于一致,这即表明本文所给的算法是有效的.
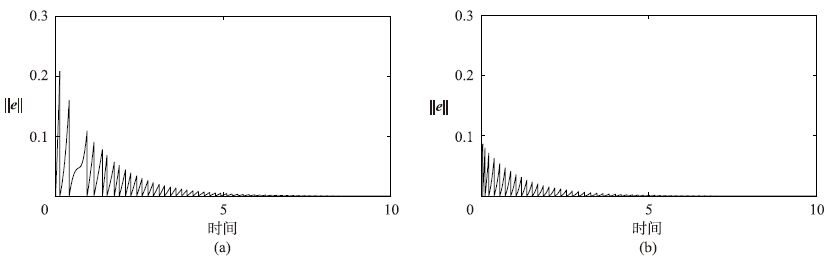
为了说明在基于事件触发控制的一致性算法中,各智能体之间只有在事件触发时刻才进行信息采样,现针对多智能体系统的误差进行分析,图 4给出了多智能体系统在两种不同拓扑结构下的误差e的演化趋势.
|
| 图 4 智能体的测量误差演化图 Figure 4 Evolution of the measurement error of the agents |
由图 4可知,在两种不同拓扑结构下,系统中每个智能体均是在状态误差达到某一特定值时才触发事件.
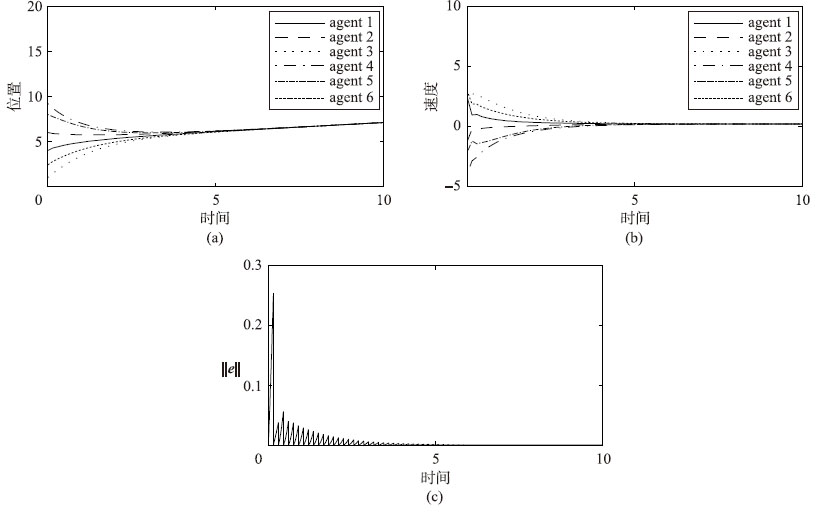
图 5给出了多智能体系统在图 1(a)下基于周期采样控制算法的仿真结果.
|
| 图 5 周期采样控制算法仿真结果 Figure 5 Simulation results of the time-triggered control algorithms |
从图 2(a)、图 3(a)和图 5(a)、图 5(b)可以看出,在同一拓扑结构下,这两种控制算法均可使得系统中所有智能体的位置和速度状态达到平均一致.另外,计算在仿真时间[0,10]内的采样数据通信量.在事件触发策略下,每个智能体发送出去的采样数据包的数量为51,整个系统的信息交换量为816,而在周期采样策略下,每个智能体产生67个采样数据包,整个系统的信息通信数为1072,也就是说采用事件触发控制算法只需大约76.12%的采样数据进行信息交换就可以使得多智能体系统在[0,10]内达到一致.从图 4(a)和图 5(c)可以看出,采用本文所提的事件触发控制算法可以减少智能体的采样次数,从而减少智能体之间的通信次数,节省网络资源.这即证明了本文所研究算法的合理性,也表明了本文的研究意义.
5 结论本文研究了二阶多智能体系统的平均一致性问题.针对周期采样控制方法存在的不足,给出了一种基于事件触发机制的控制算法.通过对智能体的状态进行分解,将系统的一致性问题转化为闭环系统的稳定性问题,并通过理论分析证明了多智能体系统在该控制算法下最终可以达到平均一致.最后,仿真实例验证了理论方案的正确性.在接下来的工作中,将进一步研究在切换有向拓扑及存在外部干扰情况下的多智能体系统的一致性问题.
| [1] | Liu X W, Lu W L, Chen T P. Consensus of multi-agent systems with unbounded time-varying delays[J]. IEEE Transactions on Automatic Control, 2010, 55 (10): 2396–2401. DOI:10.1109/TAC.2010.2054770 |
| [2] | 邵浩宇, 胡爱花. 基于事件驱动控制的非线性多智能体的一致性[J]. 信息与控制, 2015, 44 (1): 38–42. Shao H Y, Hu A H. Consensus of nonlinear multi-agent systems with event-triggered control[J]. Information and Control, 2015, 44 (1): 38–42. |
| [3] | Gao Y P, Wang L. Sampled-data based consensus of continuous-time multi-agent systems with time-varying topology[J]. IEEE Transactions on Automatic Control, 2011, 56 (5): 1226–1231. DOI:10.1109/TAC.2011.2112472 |
| [4] | Liu Z W, Guan Z H, Shen X M, et al. Consensus of multi-agent networks with a periodic sampled communication via impulsive algorithms using position-only measurements[J]. IEEE Transactions on Automatic Control, 2012, 57 (10): 2639–2643. DOI:10.1109/TAC.2012.2214451 |
| [5] | 丁磊. 不同数据触发机制下的多智能体系统一致性及H∞滤波[D]. 大连:大连海事大学, 2014. Ding L. Consensus and H∞filtering of multi-agent systems based on various data-triggering mechanisms[D]. Dalian:Dalian Maritime University, 2014. |
| [6] | Yu W W, Zheng W X, Chen G R, et al. Second-order consensus in multi-agent dynamical systems with sampled position data[J]. Automatica, 2011, 47 (7): 1496–1503. DOI:10.1016/j.automatica.2011.02.027 |
| [7] | 胡松林. 基于事件触发机制的网络化控制系统的分析和综合[D]. 武汉:华中科技大学, 2012. Hu S L. Analysis and synthesis of networked control systems with event-triggering scheme[D]. Wuhan:Huangzhong University of Science and Technology, 2012. |
| [8] | Arzen K E. A simple event-based PID controller[J]. Proceedings of IFAC World Congress, 1999, 18 : 423–428. |
| [9] | Tabuada P. Event-triggered real-time scheduling of stabilizing control tasks[J]. IEEE Transactions on Automatic Control, 2007, 52 (9): 1680–1685. DOI:10.1109/TAC.2007.904277 |
| [10] | Fan Y, Feng G, Wang Y, et al. Distributed event-triggered control of multi-agent systems with combinational measurements[J]. Automatica, 2013, 49 (2): 671–675. DOI:10.1016/j.automatica.2012.11.010 |
| [11] | Dimarogonas D V, Johansson K H. Event-triggered control for multi-agent systems[C]//Proceedings of the 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference. Piscataway, NJ, USA:IEEE, 2009:7131-7136. |
| [12] | Dimarogonas D V, Frazzoli E. Distributed event-triggered control strategies for multi-agent systems[C]//Proceedings of the 47th Annual Allerton Conference on Communication, Control, and Computing. Piscataway, NJ, USA:IEEE, 2009:906-910. |
| [13] | Dimarogonas D V, Frazzoli E, Johansson K H. Distributed event-triggered control for multi-agent systems[J]. IEEE Transactions on Automatic Control, 2012, 57 (5): 1291–1297. DOI:10.1109/TAC.2011.2174666 |
| [14] | Wang Z X, Fei M R, Du D J, et al. Event-triggered average consensus for multiagent systems with time-varying delay[J]. Mathematical Problems in Engineering, 2014, 19 (2): 281–297. |
| [15] | Hu J P. Second-order event-triggered multi-agent consensus control[C]//Proceedings of the 201231st Chinese Control Conference. Piscataway, NJ, USA:IEEE, 2012:6339-6344. |
| [16] | Yan H C, Shen Y C, Zhang H, et al. Decentralized event-triggered consensus control for second-order multi-agent systems[J]. Neurocomputing, 2014, 133 (8): 18–24. |
| [17] | Wang X F, Lemmon M D. Event-triggering in distributed networked control systems[J]. IEEE Transactions on Automatic Control, 2011, 56 (3): 586–601. DOI:10.1109/TAC.2010.2057951 |
| [18] | Xie D S, Xu S Y, Chu Y M, et al. Event-triggered average consensus for multi-agent systems with nonlinear dynamics and switching topology[J]. Journal of the Franklin Institute-Engineering and Applied Mathematics, 2015, 352 (3): 1080–1098. DOI:10.1016/j.jfranklin.2014.11.004 |
| [19] | Yue D, Yin X X. Adaptive event-triggered consensus for multi-agent systems with stochastic switching topologies and delays[C]//IEEE International Symposium on Industrial Electronics. Piscataway, NJ, USA:IEEE, 2013:1-6. |
| [20] | Mu N K, Liao X F, Huang T W. Event-based consensus control for a linear directed multiagent system with time delay[J]. IEEE Transactions on Circuits and Systems Ⅱ-Express Briefs, 2015, 62 (3): 281–285. DOI:10.1109/TCSII.2014.2368991 |
| [21] | Zhang Z Q, Hao F, Zhang L, et al. Consensus of linear multi-agent systems via event-triggered control[J]. International Journal of Control, 2014, 87 (6): 1243–1251. DOI:10.1080/00207179.2013.873952 |
| [22] | Xie D S, Yuan D M, Lu J W, et al. Consensus control of second-order leader-follower multi-agent systems with event-triggered strategy[J]. Transactions of the Institute of Measurement and Control, 2013, 35 (4): 426–436. DOI:10.1177/0142331212454046 |
| [23] | Li H Q, Liao X F, Huang T W, et al. Event-triggering sampling based leader-following consensus in second-order multi-agent systems[J]. IEEE Transactions on Automatic Control, 2015, 60 (7): 1998–2003. DOI:10.1109/TAC.2014.2365073 |



