1 引言
极限学习机算法[1]是针对单个隐藏层的前馈型神经网络的监督型学习算法[2-3].传统的神经网络学习算法(如BP,back propagation)通常需要人为设置大量的网络训练参数,很容易陷入局部最优,而且基于梯度下降学习方法还存在需要多次迭代的缺点[4-5].与传统BP相比,极限学习机只需要设置网络的隐层节点个数,在算法执行过程中不需要调整网络的输入权值以及隐层神经元的阈值,并且产生唯一的最优解,因此具有训练参数少、学习速度快[6-7]且泛化性能好等优点[8],文[9-11]通过实验验证了极限学习机在分类上相对于BP和支持向量机(support vector machine,SVM)的优势.
但是极限学习机也存在着一些自身的不足,如极限学习机网络的输入权值以及隐层神经元的阈值是随机获取的,在一定程度上导致网络稳定性差.当训练数据中存在离群点或者扰动时,隐层输出矩阵存在病态问题,导致网络鲁棒性变差、泛化性能和预测精度降低[12].
极限学习机可以分为固定型极限学习机(extreme learning machine,ELM)和增量型极限学习机(I-ELM)[13].ELM只需要一次计算就可结束训练过程,因此训练时间非常短,但是隐层神经元数目存在最佳选取值问题.由于ELM的训练过程可以被看作是求解线性方程组,所以文[14]提出了一种选择使输出矩阵满秩的输入权值和阈值的改进方法,文[15]提出了一种牛顿算法用于求解并优化输出权值.它适用于分类[16]和在线故障诊断[17]和在线实时预测[18-19]等.
而I-ELM已经被证明随着隐层节点数目的递增,I-ELM的输出误差逐渐变小并趋向于0.但是I-ELM中输出权值的计算次数等于隐层节点数目,因此训练速度不如ELM.它适用于在线连续学习过程中做回归和分类问题
等[20].从I-ELM训练过程增加神经元个数的判断依据出发,由于I-ELM训练过程中,输入权值以及隐层神经元的阈值是随机取得,存在部分隐层神经元的输出权值过小,使其对网络输出贡献很小,使得网络的学习速度变慢,进而影响增加隐层神经元的个数,使网络变得更复杂,而且降低了网络的稳定性.为此,文[21]基于凸优化概念提出了凸增量极限学习机(CI-ELM),它与I-ELM的本质区别在于: 增加一个隐层节点后I-ELM函数为fn=fn-1+βnhn,而CI-ELM函数为fn=(1-βn)fn-1+βnhn,基于这种改变并结合I-ELM的原理,CI-ELM求解权值和余差的公式也做了相应的修改.文[22]基于选取使余差最小的输入权值和阈值提出了提升随机搜索的增量型极限学习机(EI-ELM),但是它的训练时间会大大增加.这两种方法都能在一定程度上改善I-ELM的泛化性.
针对I-ELM的缺点,本文提出了一种给隐层输出加上一个偏置求得最优权值的改进方法(improved incremental extreme learning machine,Ⅱ-ELM),该偏置与隐层神经元阈值的本质区别是: 在Ⅱ-ELM的学习步骤中,阈值先于隐层输出并且是随机的,而偏置是后于隐层输出且与网络的误差存在某种函数关系,是存在最优解的.本文分析证明了该偏置的存在性,并且通过与I-ELM、CI-ELM和EI-ELM在回归问题上的仿真对比以及与I-ELM在分类问题上的仿真对比,验证所提出的改进方法的有效性.
2 I-ELM算法的描述本文研究的I-ELM网络如图 1所示.

|
| 图 1 I-ELM网络 Figure 1 I-ELM network |
如图 1所示,I-ELM网络有m个输入n个输出.a表示当前隐层神经元的输入权值,是一个1×m的矩阵,它的元素为[-1,1]之间的随机值; bL表示第L个隐层神经元的阈值,当其隐层神经元选择式(1)对应的加法型激励函数时,bL取值为[-1,1]之间的随机数; 而选择式(2)对应的激励函数时,bL取值为[0,0.5]之间的随机数.给定训练集为{(Xi,Yi)}(i=1,2,…,N)(N为训练样本的个数).其中X为m×N的矩阵,它表示N组数据的输入; Y为n×N的矩阵,它表示N组数据的输出.
隐层神经元的激励函数可自己选择,本文选择的加法隐层神经元的激励函数为

|
(1) |
本文选择的径向基隐层神经元的激励函数为

|
(2) |
若x为矩阵,则$x.\widehat{{}}2$表示将x矩阵里每个元素平方.
设最大隐层神经元个数为M,期望误差(即余差平方均值的开方)为ε,余差(即网络的实际输出与目标之间的差值矩阵)E的初值是输出Y.隐层神经元个数L从1开始增加.
I-ELM的学习步骤如下:
当L<M且误差大于期望误差时:
(1) L=L+1.
(2) 随机获取当前隐层神经元的输入权值a和阈值b.
(3) 计算当前隐层神经元激励函数ɡ(x)的输入x.
1) 加法隐层神经元: 将b扩展成一个1×N的矩阵b(每列都相同),然后计算:

|
(3) |
2) 径向基隐层神经元: 将a扩展成一个N×m的矩阵(每行都相同),然后计算:

|
(4) |
(4) 计算当前的隐层输出:
1) 加法隐层神经元:

|
(5) |
2) 径向基隐层神经元:

|
(6) |
(5) 然后计算出该隐层神经元的输出权值:

|
(7) |
(6) 最后计算添加一个隐层神经元之后的余差:

|
(8) |
根据式(7)所求得的输出权值能使网络的误差下降最快,后面将对此进行证明.重复上述操作,直到误差小于期望误差时停止学习; 若误差一直大于期望误差,则当L>M时停止学习,这是由于输入权值a和阈值b的随机性造成的,这时应该重新开始学习.
最后,根据给定的测试集{(Xi,Yi)}(i=1,2,…,J)(J为测试样本的个数),测试训练好的网络是否达到要求.若达到要求,则认为该I-ELM网络训练成功.
上述I-ELM原理的分析中,式(7)求得的β可以使H最接近E(即网络误差下降最快)[1, 13].这里,阐述一下证明过程.为了方便证明这一点,假设只有一个输出,即E为一个1×N的矩阵,而H也为一个1×N的矩阵.
证明 当E=[e1,e2,…,eN],H=[h1,h2,…,hN]时
(1) 此时的输出权值为一个标量,记为β.由式(7)可知:

|
(9) |
(2) 它们的余差由式(8)可知:

|
(10) |
(3) 它们的误差记为Z,由式(10)可知:

|
(11) |
(4) 求使误差Z最小的权值β:
对函数:

|
(12) |
求导得出:
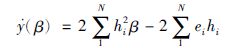
|
(13) |
由式(13)中
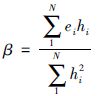
|
(14) |
对比式(14)与式(9)可知,式(7)求得的输出权值β可以使网络误差最小,即误差下降速度最快.
通过上面分析可知,由于网络输入权值以及隐层神经元的阈值的随机取得,使得隐层输出H也是随机的,而余差E是已知的.所以,当求输出权值β时,会出现
针对上面对I-ELM网络误差下降速度慢的原因分析,本文提出给隐层输出加上了一个偏置m,使隐层输出H中的每个元素加m后,再计算输出权值k.这样通过m调节隐层输出H的方法,可以极大程度地避免求得输出权值过小、隐层神经元无效的情况,并因此提高I-ELM网络的误差下降速度.
为了方便说明改进效果,假设网络只有一个输出.例如当H=[0.1,0.2,0.3,0.4],E=[0.66,0.33,0,-0.33]时,由式(7)得到I-ELM网络的输出权值为0,误差没变化,该隐层节点无效.而改进后,可以通过调节m值改变H.当m=-0.3时,H=[-0.2,-0.1,0,0.1],相对应输出权值k=-3.3,此时网络的误差下降到0.
当然,并不是每一个m取值都能使网络的误差下降得比之前还小; 有时也会出现m值为0时,网络是最优的,这就意味着该隐层节点不需要加偏置m.例如当H=[0.1,0.2,0.3,0.4],E=[0.2,0.4,0.6,0.8]时,相对应输出权值k=2,此时网络的误差下降到0,添加偏置m反而会使网络变差.针对这些问题,下面将讨论该如何选取m值.
当E=[e1,e2,…,eN],H=[h1,h2,…,hN],偏置为m时,假设M=[(h1+m),(h2+m),…,(hN+m)].
(1) 先求E和M之间的误差Z′:
由式(7)可知此时的输出权值应为

|
(15) |
由式(11)可知,此时误差Z′为

|
(16) |
将式(15)的k值代入式(16)得:

|
(17) |
由式(16)可知,不管m取何值,Z′根号里的式子都是大于等于0的,即m的取值范围是(-∞,+∞).
(2) 求使Z′最小的m值:
为了使Z′最小,对函数求导:

|
(18) |
设


|
(19) |
设c1=a1b2-a2b1,c2=2(a1b3-a3b2),c3=a2b3-a3b2,为求得式(18)中y(m)的极值,令式(19)中(m)=0.
假设导数$\dot{y}=\left( m \right)$无解,即b1m2+b2m+b3=0.又


式(19)求得的极值点不仅是式(18)中y(m)的极值,而且是式(16)和式(17)中Z′的极值.而使Z′最小的m值在极值点、导数无解的点和边界点中,式(16)和式(17)中Z′的边界点是m=±∞,且在两个边界点上的Z′值是相同的.但是m取±∞时,由式(15)可知输出权值k为0,这是不符合要求的.又因为不存在使导数(m)无解的点.所以,当使Z′最小的m值在极值点中时,则取该m值并计算对应的输出权值k; 当使Z′最小的m值在边界点中时,该隐层节点无效,将其删除; 当Z′是恒定值(后面会证明此时隐层输出矩阵H里的元素都相等,所以这种情况出现的概率极小)时,无论m为何值,网络的误差下降程度都一样,取m=0,并计算对应的输出权值k.
下面分析y(m)极值点的几种存在类型:
(1) 当c1≠0时:
此时相当于解一个一元二次方程,先判断其解的存在性,其中a22=4a1a3.它的判别式为

|
(20) |
由于Δ≥0,所以极值点存在,得到两个极值点:

|
(21) |

|
(22) |
当Δ>0时,这两个极值点不相同,一个是极小值,一个是极大值.此时,$\dot{y}=\left( m \right)$=-(m-m1)(m-m2)/(b1m2+b2m+b3)2.当(m)>0时,误差Z′单调上升; 当(m)<0时,误差Z′单调下降.由上可知,m从负无穷大到正无穷大取值时,误差Z′会先从误差e(添加该隐层神经元前的误差)逐渐上升到极大值再逐渐下降到极小值最后再逐渐上升到误差e(或者是从误差e逐渐下降到极小值再逐渐上升到极大值最后再逐渐下降到误差e).因此,其中的极小值点能使误差Z′最小.将求得的两个极值点代入式(17),取其中使式(17)中Z′最小的极值点m,即为极小值点,再通过式(15)求得相应的输出权值k.
当Δ=0时,这两个极值点相同.此时

|
(23) |
又因为a22=4a1a3,所以只要a1、a2、a3中有一个为0,其它两个也为

|
(24) |
又a1、a3、b1、b3都是大于0的,由式(24)转换得:

|
(25) |
又由于a22=4a1a3,假设4b1b3≥b22,4b1b3≥b22两边再同时除以a22得到:

|
(26) |
所以只要证明4b1b3≥b22,即证明

|
(27) |
将式(27)代入式(24)得:

|
(28) |
这时c1=0.当c1≠0时,假设Δ=0,得到c1=0与条件不符,假设错误,所以c1≠0时,Δ≠0.
现在证明
证明1
1) N=2时,很容易得到:

|
(29) |
2) 假如N=k时:

|
(30) |
3) 那么由式(30)得,当N=k+1时:
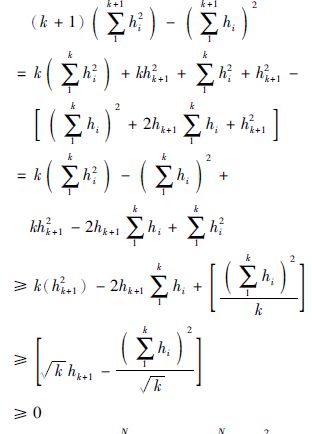
|
(31) |
综上所述,
(2) 当c1=0且c2≠0时:
得到一个极值点:

|
(32) |
由于c1=0,又

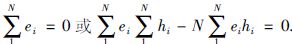
当

当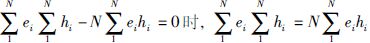


|
前面已证明

(3) 当c1=0、c2=0时: c1=a1b2-a2b1=0,c2=2(a1b3-a3b1)=0.
当a1=0时b1=N≠0,所以a2=0、a3=0,此时c3=a2b3-a3b2=0; 当a1≠0时,c3=a2b3-a3b2=a2a3b1/a1-a2a3b1/a1=0.
因此当c1=0、c2=0时,c3=0.此时$\dot{y}\left( m \right)=0$,误差Z′是一个固定值.m值取0,并计算对应的输出权值k.
由证明2可知,只有当隐层输出矩阵H里的元素都相等时,c1=c2=c3=0,所以这种情况出现的概率极小.
证明2 当c1=c2=c3=0时,h1=h2=…=hN.
1) 当c1=c2=c3=0时:
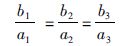
|
(33) |
即为
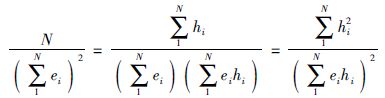
|
(34) |
2) 由式(34)得出:

|
(35) |
3) 由式(35)和前面证明过的定理

以上是关于调节输出矩阵H的偏置m值和对应的输出权值k的取法.通过上述分析可知,Ⅱ-ELM这种方法得到的是使误差最小的点,而I-ELM相当于取的是偏置m=0时的点,所以如果在相同的初始误差下添加一个神经元,Ⅱ-ELM肯定比I-ELM的误差下降得多.
Ⅱ-ELM的学习步骤只需要将I-ELM学习步骤中的第(5)步改为: 求得该隐层神经元的隐层输出偏置m和输出权值k,其它的学习步骤和I-ELM一样.因此,每添加一个神经元,Ⅱ-ELM和I-ELM在学习的时间上基本上差不多,又由于Ⅱ-ELM比I-ELM的误差下降得多,所以在相同的误差要求下,Ⅱ-ELM学习速度比I-ELM快.
4 仿真研究本文对Ⅱ-ELM和I-ELM进行了回归和分类仿真实验,并对其结果进行对比,此外还对比了Ⅱ-ELM、CI-ELM和EI-ELM在回归问题上改善I-ELM的程度.本文的实验数据都来自于UCI数据库数据.为了方便对比Ⅱ-ELM、CI-ELM和EI-ELM对I-ELM的改善程度,实验数据基本与CI-ELM和EI-ELM这两种改进方法所用数据一致.数据经过归一化后的范围是(-1,1),关于Ⅱ-ELM和I-ELM的所有仿真都是在MATLAB R2009a,3.0 GHz CPU和1GRAM的PC机上完成.
表 1给出了本文实验的4个真实的回归问题的说明.图 2给出了添加3 000个隐层神经元时,I-ELM、Ⅱ-ELM、CI-ELM和EI-ELM网络的测试误差下降曲线.从图 2可以发现,不管是用加法隐层神经元还是径向基隐层神经元,Ⅱ-ELM的收敛速度都比I-ELM、CI-ELM和EI-ELM快得多.
| 名称 | 训练数据 | 测试数据 | 属性 |
| Abalone | 2 000 | 2 177 | 8 |
| Auto price | 80 | 79 | 15 |
| Boston housing | 250 | 256 | 13 |
| Machine CPU | 100 | 109 | 6 |

|
| 图 2 用Abalone数据训练I-ELM网络、Ⅱ-ELM网络CI-ELM网络EI-ELM网络的对比 Figure 2 Comparison of I-ELM network,Ⅱ-ELM network,CI-ELM network and EI-ELM network on Abalone data |
表 2、表 3和表 4分别给出了添加200个隐层神经元时,训练I-ELM、Ⅱ-ELM、CI-ELM、EI-ELM四个真实的回归问题的结果: 训练时间(反映学习速度)、测试误差(反映网络的测试精度)、测试误差的方差(反映网络的稳定性).结果是在同一实验条件下对每个回归问题训练20次以上取其平均值得到的.最后,表 2、表 3和表 4还给出了只添加30个隐层神经元时的Ⅱ-ELM训练结果,用Ⅱ-ELM(30)表示.
| 数据名称 | Sigmoid (training time) | RBF (training time) | ||||||||
| Ⅱ-ELM(30) | Ⅱ-ELM | CI-ELM | EI-ELM | I-ELM | Ⅱ-ELM(30) | Ⅱ-ELM | CI-ELM | EI-ELM | I-ELM | |
| Abalone | 0.045 3 | 0.278 5 | 0.453 1 | 2.580 1 | 0.221 4 | 0.088 5 | 0.586 8 | 1.020 9 | 5.600 6 | 0.503 0 |
| Auto price | 0.006 6 | 0.043 8 | 0.060 0 | 0.314 1 | 0.032 9 | 0.007 5 | 0.050 6 | 0.085 8 | 0.403 1 | 0.046 8 |
| Boston housing | 0.010 2 | 0.068 4 | 0.121 1 | 0.433 2 | 0.051 5 | 0.011 3 | 0.075 2 | 0.127 6 | 0.797 2 | 0.065 7 |
| Machine CPU | 0.004 7 | 0.031 3 | 0.044 2 | 0.311 2 | 0.023 4 | 0.007 9 | 0.052 8 | 0.087 6 | 0.411 4 | 0.044 7 |
| 数据名称 | Sigmoid (testing RMSE) | RBF (testing RMSE) | ||||||||
| Ⅱ-ELM(30) | Ⅱ-ELM | CI-ELM | EI-ELM | I-ELM | Ⅱ-ELM(30) | Ⅱ-ELM | CI-ELM | EI-ELM | I-ELM | |
| Abalone | 0.080 9 | 0.078 9 | 0.082 8 | 0.081 8 | 0.092 0 | 0.087 2 | 0.079 4 | 0.085 8 | 0.082 9 | 0.093 8 |
| Auto price | 0.105 5 | 0.089 2 | 0.092 7 | 0.089 6 | 0.097 7 | 0.110 3 | 0.095 5 | 0.119 6 | 0.113 9 | 0.126 1 |
| Boston housing | 0.120 1 | 0.104 3 | 0.110 6 | 0.105 5 | 0.116 7 | 0.118 1 | 0.105 1 | 0.145 5 | 0.107 7 | 0.132 0 |
| Machine CPU | 0.045 1 | 0.042 0 | 0.048 9 | 0.046 6 | 0.050 4 | 0.046 6 | 0.032 5 | 0.058 9 | 0.055 4 | 0.067 4 |
| 数据名称 | Sigmoid (standard deviation of testing RMSE) | RBF (standard deviation of testing RMSE) | ||||||||
| Ⅱ-ELM(30) | Ⅱ-ELM | CI-ELM | EI-ELM | I-ELM | Ⅱ-ELM(30) | Ⅱ-ELM | CI-ELM | EI-ELM | I-ELM | |
| Abalone | 0.001 9 | 0.000 5 | 0.003 0 | 0.002 0 | 0.004 6 | 0.002 2 | 0.001 8 | 0.002 9 | 0.002 7 | 0.015 2 |
| Auto price | 0.012 6 | 0.005 0 | 0.008 3 | 0.002 2 | 0.006 9 | 0.010 6 | 0.004 3 | 0.017 7 | 0.018 9 | 0.025 5 |
| Boston housing | 0.007 5 | 0.003 4 | 0.005 9 | 0.009 8 | 0.011 2 | 0.007 5 | 0.002 0 | 0.007 6 | 0.008 4 | 0.012 6 |
| Machine CPU | 0.005 5 | 0.004 0 | 0.008 4 | 0.006 0 | 0.007 9 | 0.008 3 | 0.005 6 | 0.011 6 | 0.014 8 | 0.017 7 |
由表 2可知: 在隐层神经元个数相同的情况下,4种算法I-ELM、Ⅱ-ELM、CI-ELM和EI-ELM学习过程所花的时间排序为: I-ELM<Ⅱ-ELM<CI-ELM<EI-ELM.一般情况下,优化I-ELM都会使I-ELM每添加一个隐层神经元学习所花的时间变长.表 2中,Ⅱ-ELM学习过程所花的时间几乎和I-ELM一样.由上述分析可得,优化算法Ⅱ-ELM相比于CI-ELM和EI-ELM,学习速度更快且几乎和原I-ELM算法学习速度一样.
由表 3可知: 在隐层神经元个数相同的情况下,4种算法I-ELM、Ⅱ-ELM、CI-ELM、EI-ELM的测试标准误差排序为: Ⅱ-ELM<EI-ELM<CI-ELM<I-ELM.由此可得: 优化算法Ⅱ-ELM相比于CI-ELM、EI-ELM、I-ELM,网络精度更高.
由表 4可知: 在隐层神经元个数相同的情况下,4种算法I-ELM、Ⅱ-ELM、CI-ELM和EI-ELM的测试标准误差的方差排序为: Ⅱ-ELM<(EI-ELM、CI-ELM)<I-ELM.由此可得,优化算法Ⅱ-ELM相比于CI-ELM、EI-ELM和I-ELM,网络更稳定.
由表 2、表 3和表 4可知: 在优化算法Ⅱ-ELM只添加30个隐层神经元,对比于其它算法添加200个隐层神经元时可以发现,在测试误差和测试误差方差相差不多的情况下,Ⅱ-ELM训练所花时间大大减少.所以,在误差要求一样的情况下,Ⅱ-ELM算法的学习速度要比CI-ELM、EI-ELM和I-ELM快.
表 5给出了本文实验的4个真实的分类问题的说明.图 3给出了Ⅱ-ELM和I-ELM添加到100个隐层神经元时,网络分类识别的正确率上升曲线.从图中可以发现,不管是用加法隐层神经元还是径向基隐层神经元,Ⅱ-ELM的正确率上升速度都比I-ELM快得多.
| 名称 | 训练数据 | 测试数据 | 属性 |
| Banknote authentication | 686 | 686 | 5 |
| Balance Scale | 313 | 312 | 5 |
| shuttle | 7 250 | 7 250 | 10 |
| glass | 107 | 107 | 10 |

|
| 图 3 I-ELM网络和Ⅱ-ELM网络对Banknote authentication数据分类的对比 Figure 3 Comparison between I-ELM network and Ⅱ-ELM network on Banknote authentication data classification |
表 6给出了Ⅱ-ELM和I-ELM添加100个隐层神经元时,训练上述4个真实的分类问题的结果: 正确率.
| 名称 | Sigmoid | RBF | ||
| Ⅱ-ELM | I-ELM | Ⅱ-ELM | I-ELM | |
| Banknote authentication | 0.982 5 | 0.696 8 | 0.981 0 | 0.689 5 |
| Balance Scale | 0.875 0 | 0.810 9 | 0.871 8 | 0.820 5 |
| shuttle | 0.859 9 | 0.796 1 | 0.857 1 | 0.796 6 |
| glass | 0.579 4 | 0.364 5 | 0.551 4 | 0.364 5 |
由表 6可知: 在隐层神经元个数相同的情况下,无论是用加法隐层神经元还是径向基隐层神经元,Ⅱ-ELM在分类正确率上都要比I-ELM高.
5 总结与展望本文给在I-ELM的隐层输出加上一个偏置m,使其网络在相同输入权值和隐层神经元阈值的条件下,网络训练的误差下降得更快,不但提高了网络的训练速度,同时还提高了测试的精度.通过对Ⅱ-ELM、CI-ELM和EI-ELM在回归问题的对比实验,结果验证了Ⅱ-ELM比CI-ELM、EI-ELM的学习速度更快、网络精度更高、网络更稳定.以及通过Ⅱ-ELM和I-ELM在回归和分类问题上的对比仿真实验,结果验证了Ⅱ-ELM无论是在回归问题上还是分类问题上都比I-ELM效果更好,较好地解决了I-ELM由于输入权值以及隐层神经元的阈值是随机取得,在训练过程中增加神经元会存在部分隐层神经元的输出权值过小,导致其对网络输出贡献很小,降低了网络的训练速度,使网络变得更加复杂的问题.
| [1] | Huang G B, Bai Z, Kasun L L C, et al. Local receptive fields based extreme learning machine[J]. IEEE Computational Intelligence Magazine, 2015, 10 (2): 18–29. DOI:10.1109/MCI.2015.2405316 |
| [2] | Huang G B, Zhu Q Y, Siew C K. Extreme learning machine:A new learning scheme of feedforward neural networks[C]//Proceedings of International Joint Conference on Neural Networks. Piscataway, NJ, USA:IEEE, 2004:985-990. |
| [3] | Huang G B, Zhu Q Y, Siew C K. Extreme learning machine:Theory and applications[J]. Neurocomputing, 2006, 70 (1/2/3): 489–501. |
| [4] | Popa C A. Enhanced gradient descent algorithms for complex-valued neural networks[C]//International Symposium on Symbolic and Numeric Algorithms for Scientific Computing. Piscataway, NJ, USA:IEEE, 2014:272-279. |
| [5] | You Z, Wang X R, Xu B. Exploring one pass learning for deep neural network training with averaged stochastic gradient descent[C]//International Conference on Acoustics, Speech and Signal Processing. Piscataway, NJ, USA:IEEE, 2014:6854-6858. |
| [6] | Yeu C W T, Lim M H, Huang G B, et al. A new machine learning paradigm for terrain reconstruction[J]. IEEE Geoscience and Remote Sensing Letiers, 2006, 3 (3): 382–386. DOI:10.1109/LGRS.2006.873687 |
| [7] | Huang G B, Lei C, Siew C K. Universal approximation using incremental constructive feedforward networks with random hidden nodes[J]. IEEE Transactions on Neural Networks, 2006, 17 (4): 879–892. DOI:10.1109/TNN.2006.875977 |
| [8] | Huang G B, Zhu Q Y, Mao K Z, et al. Can threshold networks be trained directly?[J]. IEEE Transactions on Circuits and Systems Ⅱ:Express Briefs, 2006, 53 (3): 187–191. DOI:10.1109/TCSII.2005.857540 |
| [9] | Tang X L, Han M. Ternary reversible extreme learning machines:The incremental tri-training method for semi-supervised classification[J]. Knowledge and Information Systems, 2010, 23 (3): 345–372. DOI:10.1007/s10115-009-0220-4 |
| [10] | Wang D H, Huang G B. Protein sequence classification using extreme learning machine[C]//Proceedings of International Joint Conference on Neural Networks. Piscataway, NJ, USA:IEEE, 2005:1406-1411. |
| [11] | Huang G B, Ding X J, Zhou H M. Optimization method based extreme learning machine for classification[J]. Neurocomputing, 2010, 74 . |
| [12] | Jun G, Yaw F C, Koon N B, et al. Quantitative diagnosis of cervical precancer using fluorescence intensity and lifetime imaging from the stroma[C]//Photonics Global Conference. Piscataway, NJ, USA:IEEE, 2012:1-5. |
| [13] | Huang G B, Chen L, Siew C K. Universal approximation using incremental constructive feedforward networks with random hidden nodes[J]. IEEE Transactions on Neural Networks, 2006, 17 (4): 879–892. DOI:10.1109/TNN.2006.875977 |
| [14] | Chen Z X, Zhu H Y, Wang Y G. A modified extreme learning machine with Sigmoidal activation functions[J]. Neural Computing and Applications, 2013, 22 (3/4): 541–550. |
| [15] | Balasundaram S. On extreme learning machine for ε-insensitive regression in the primal by Newton method[J]. Neural Computing and Applications, 2013, 22 (3): 559–567. |
| [16] | Ma X, Zhou S K, Li Y B. Incremental human action recognition with online sequential extreme learning machine[J]. International Journal of Advancements in Computing Technology, 2013, 5 (9): 155–163. DOI:10.4156/ijact |
| [17] | Yin G, Zhang Y T, Li Z N. Online fault diagnosis method based on incremental support vector data description and extreme learning machine with incremental output structure[J]. Neurocomputing, 2014, 128 : 224–231. DOI:10.1016/j.neucom.2013.01.061 |
| [18] | 马超, 张英堂. 在线核极限学习机及其在时间序列预测中的应用[J]. 信息与控制, 2014, 43 (5): 624–629. Ma C, Zhang Y T. Online kernel extreme learning machine and its application to time series prediction[J]. Information and Control, 2014, 43 (5): 624–629. |
| [19] | 曹卫华, 李熙, 吴敏, 等. 基于极限学习机的热轧薄板轧制力预测模型[J]. 信息与控制, 2014, 43 (3): 272–275. Cao W H, Li X, Wu M, et al. A rolling force prediction model for hot rolled sheets based on extreme learning machine[J]. Information and Control, 2014, 43 (3): 272–275. |
| [20] | Guo L, Hao J H, Liu M. An incremental extreme learning machine for online sequential learning problems[J]. Neurocomputing, 2014, 128 : 50–58. DOI:10.1016/j.neucom.2013.03.055 |
| [21] | Huang G B, Chen L. Convex incremental extreme learning machine[J]. Neurocomputing, 2007, 70 (16/17/18): 3056–3062. |
| [22] | Huang G B, Chen L. Enhanced random search based incremental extreme learning machine[J]. Neurocomputing, 2008, 71 (16/17/18): 3460–3468. |



