1 引言
低压氮气是钢铁生产过程中重要的保护气体,合理的对低压氮气系统进行有效地预测及调度可以提高低压氮气的使用效率,节约生产成本.然而由于生产现场管网情况复杂,难以建立基于运行机理的预测模型对低压氮气系统管网压力进行预测.随着工业信息化的进展,钢铁企业现场的实时数据库中积累了越来越多的与生产和用能相关的数据,基于数据的方法越来越受到该领域研究人员的关注.
目前基于数据的冶金能源系统预测已存在大量研究.其中神经网络方法有前馈神经网络[1]和回声状态神经网络(echo state network,ESN)[2]等.然而,由于神经网络方法需要的训练数据量大、 计算消耗时间长,在实际应用中效果并不稳定.最小二乘支持向量机(least squares support vector machine,LSSVM)[3]由于其解决了小样本、 高维度、 非线性等问题,同时具有算法复杂度低,运算速度快等优点,在回归建模上有着广泛的应用[4-7].文[8]建立了基于数据的LSSVM的柜位预测模型.文[9]建立了一个具有多输出的LSSVM回归模型对转炉煤气系统多柜柜位进行预测.文[10]则将LSSVM由单核扩展为多核来进行能源系统数据的预测.然而在氮气系统的管网中,由于用户消耗量对管网压力的影响存在一定时间的延迟,因此需要考虑压力与其影响因素的延迟相关性,而以上这些文献并未将该问题加以考虑.
目前针对数据相关性的量化分析方法,有马氏距离[11]、 欧氏距离[12]、 相关系数[13]等,而其中相关系数方法的使用更为普遍,但也无法直观表述两种影响因素的内在关联.因果关系(Causality)是事物发展的重要规律,Granger提出的Granger Causality[14]方法迅速在金融时间序列分析[15]、 时间序列的降维[16]等领域得到应用.然而,Granger Causality由于其解决问题的单一性,无法直接用来对工业系统进行建模.Pearl于2000年提出了Causality模型[17],由于其直观的表达方式,目前在面部识别[18]、 知识发现[19-20]、 系统诊断[21]方面都有着一定的应用.但以上研究的问题在于,并不能将系统的延迟很好地融入所确立的模型中.
本文根据冶金能源系统中氮气管网的实际情况,建立了低压氮气管网的Causality模型.鉴于影响因素的消耗对管网压力影响存在延迟的特点,本文提出了一种基于输入延迟的多核LSSVM对管网压力进行建模预测.为了表明本文方法在趋势和数值的预测上都具有较高的精度,使用某企业低压氮气管网压力的真实数据,将4种方法的结果进行对比: 第1种方法为使用相关系数计算延迟后用原始LSSVM进行预测; 第2种方法使用本文方法计算延迟后用原始LSSVM进行预测; 第3种方法使用相关系数方法计算延迟后用多核LSSVM进行预测; 第4种为本文方法.对比实验结果说明了本文所建立的模型在压力预测上与其它方法相比具有较高的精度.
2 问题描述冶金企业是能源消耗大户,目前钢铁企业通过保证管网的压力来为转炉炼钢持续提供低压氮气.如图 1为低压氮气系统的结构简图.从图 1中可以看出,制氧机分离出的低压氮气输入管网中,供给各个用户使用.
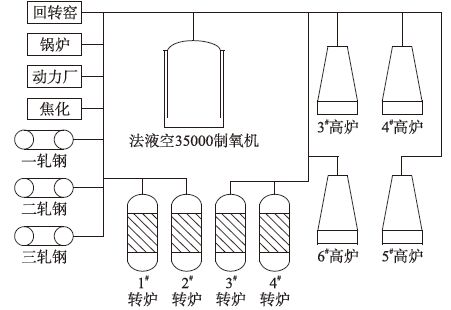
|
| 图 1 氮气系统结构简图 Figure 1 Structure of the nitrogen system |
其中,转炉使用低压氮气量是对管网压力产生重要影响的因素.目前,冶金企业中的能源调度基本是调度人员依靠自身的经验来进行调整.然而,由于调度人员经验上存在差异并且实际炼钢的生产周期和低压氮气的使用量并未严格按照生产计划进行,导致了一段时间的生产过后,管网压力便会出现不足的情况.此时为了保证炼钢的正常进行,需向外部空分企业购买额外的氮气,不仅是对能源的浪费,同时也大大增加了炼钢成本.因此,根据当前低压氮气的使用情况,对管网压力进行准确的预测,不仅可以为调度人员的后续调度提供指导,而且对于钢铁企业节约能源、 降低成本有着重要的意义.
3 基于Causality的延迟时间计算鉴于其建立准确的机理模型十分困难,本文通过基于数据的方法建立了基于影响因素的压力预测模型进行分析.在模型中,影响因素为压力和转炉使用低压氮气流量,因此需要分别计算两种影响因素的延迟.基于这些实际情况,本文建立了氮气管网压力与影响因素延迟的因果图模型如图 2所示.
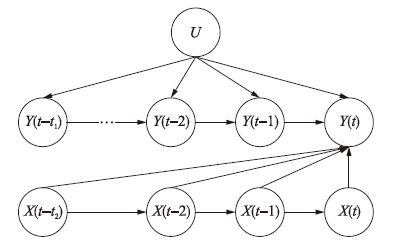
|
| 图 2 氮气管网压力与影响因素延迟关系的因果模型 Figure 2 Causal model of the relationship between the pressure of nitrogen pipe and the factors with time delay |
图 2中,节点U代表外界不可控因素,Y代表低压氮气管网压力,X则代表转炉炼钢过程中的低压氮气消耗量.图中箭头代表该因果图内因果关系的方向,由因指向果.图 2代表的含义是,外界的不可控因素,压力自身的历史数值与当前及历史时刻的影响因素流量都是导致管网压力改变的原因.
鉴于此种情况,本文提出了一种基于Causality的延迟时间计算方法,并且给出了对应的约束条件.方法步骤如下:
1) 计算压力本身的延迟时间,定义条件概率如下式所示:
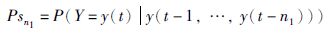
|
(1) |
其中,n1代表可能的延迟时间范围,y为管网压力,Psn1代表在时间延迟为n1时与当前工况匹配的概率.根据现场调研,一般取n1∈[0,10].在计算过程中,需满足条件:
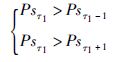
|
(2) |
即当延迟时间为τ1时,时间粒度[y(t),…,y(t-n1)]与当前工况最为吻合.
2) 计算转炉使用氮气流量相对于压力的延迟时间.定义概率:
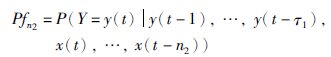
|
(3) |
表示在确定了压力自身的延迟时间情况下,加入影响因素xt,该时间粒度与当前的工况相匹配的概率.其中n2为可能的延迟时间范围,取n2∈[0,10].其满足的约束条件应为
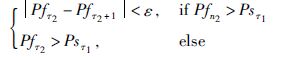
|
(4) |
上式考虑了2种情况: 第1种是当加入影响因素序列xt时,在可能的延迟时间范围之内与当前工况的匹配程度均大于没有影响因素的情况.此时应选取因果关系趋于平稳的时间点τ2作为因素的时间延迟,取ε=10-4.第2种情况是当加入影响因素序列xt时,在可能的延迟时间范围之内,加入影响因素后该时间粒度代表的生产过程与当前工况的匹配程度相比较未加影响因素之前互有高低,此时则应当取最后一个Pfn2>Psτ1的时刻作为因素延迟τ2.
4 基于影响因素延迟的多核LSSVM 4.1 基于延迟关系的训练样本构造本文根据不同影响因素的训练样本分别进行构造.假设选取N条训练样本,则训练样本构造形式如下:
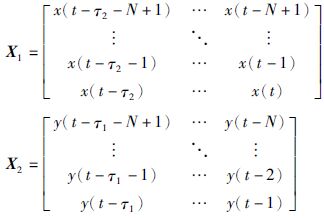
|
(5) |
测试集构造如下:
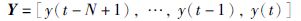
|
(6) |
由于原始的LSSVM并未针对影响因素模型进行单独分析,且未完全考虑到样本的多样性.针对低压氮气管网模型的特殊性,本文提出了一种基于影响因素延迟的多核最小二乘支持向量机.该方法根据影响因素的不同,分别构造训练样本,每个训练样本都对应一个核函数,其回归模型可修改为
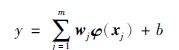
|
(7) |
式(7)中,y表示模型的输出变量,b为偏置量,xj=(x1,x2,…,xτj)表示模型的m个影响因素,其中j=1,2,…,m,延迟分别为τj,φ与wj分别为第j个影响因素对应的非线性映射函数和权重,本文均采用高斯核函数作为非线性映射函数.基于影响因素的多核最小二乘支持向量机的求解可归结为一个带约束的优化问题:
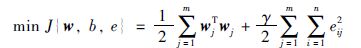
|
(8) |
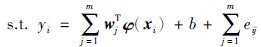
|
(9) |
式(8)中,γ表示惩罚系数,i为训练样本数据点序数,n为样本条数,eij为第j个输入变量对应的样本拟合误差.求解该优化问题通常引入拉格朗日乘子α将约束优化问题转化为无约束优化问题:
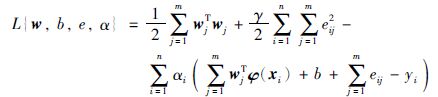
|
(10) |
消去e和ω得到方程组:
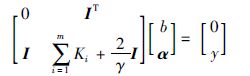
|
(11) |
式(11)中,Ki=φT(xi)φ(xj)为第i个影响因素对应的核函数,文中均采用高斯核函数,I为n维单位阵且I=[1,1,…,1]T.根据上式求解可得回归模型:
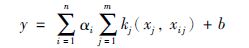
|
(12) |
根据以上描述,本文算法流程如图 3所示.
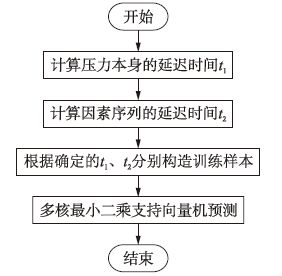
|
| 图 3 算法流程图 Figure 3 Steps of the algorithm |
为了验证本文所提方法的有效性,以国内某钢铁企业的低压氮气系统作为研究对象,从生产现场数据库中提取2014年1月的2 000个数据作为延迟时间的计算样本,然后从其中取出800个有效样本用于建模.在正常生产的情况下,低压氮气的压力需要高于940 kPa.而当压力低于950 kPa时,调度人员就需要根据现场的实际情况来对生产进行合理调度.本文将对生产现场正常工况和超限工况两种不同的情况分别进行对比实验加以验证.
为了表明本文方法对压力预测的有效性,采用均方根误差(root mean square error,RMSE)和平均绝对百分比误差(mean absolute percentage error,MAPE)对预测结果进行统计.其定义如式(13)和式(14)所示:
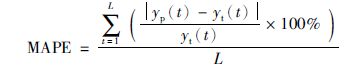
|
(13) |
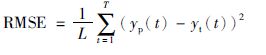
|
(14) |
其中yp(t)为预测值,yt(t)为真实值,L为预测长度.
5.1 正常工况下的时间延迟计算选取正常工况下低压氮气管网压力作为预测目标,根据本文方法计算得到压力自身的延迟时间τ1=5和转炉低压氮气使用流量的延迟时间τ2=4.相关系数方法可得到τ1=1和τ2=1,其中相关系数约束条件γ=0.4.根据十折交叉验证方法[22]分别选取原始LSSVM以及多核LSSVM的参数如表 1所示.
| 预测方法 | 核函数
宽度1 | 核函数
宽度2 | 惩罚系数 |
| 相关系数,原始LSSVM | 5.87 | - | 773.54 |
| Causality,原始LSSVM | 6.12 | - | 869.72 |
| 相关系数,多核LSSVM | 6.54 | 6.15 | 1 015.85 |
| 本文方法 | 6.32 | 6.18 | 1 004.75 |
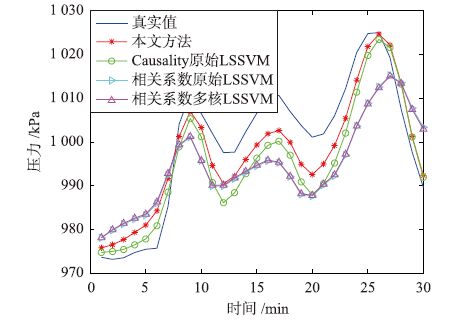
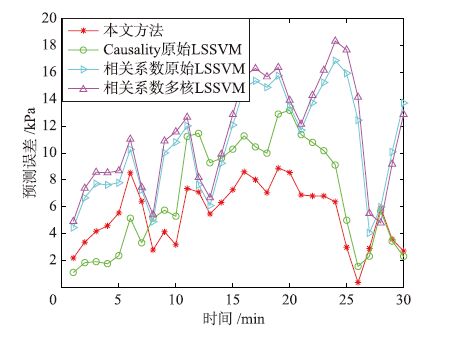
通过4种方法进行预测,结果如图 4所示,误差比较如图 5所示,误差统计结果如表 2所示.
|
| 图 4 正常工况下预测结果对比 Figure 4 Comparison of the predicted results under the normal condition |
|
| 图 5 正常工况下预测误差对比 Figure 5 Comparison of the predicted errors under the normal condition |
| 预测方法 | MAPE | RMSE /kPa |
| 相关系数,原始LSSVM | 0.010 6 | 11.277 4 |
| Causality,原始LSSVM | 0.006 8 | 7.905 1 |
| 相关系数,多核LSSVM | 0.010 5 | 11.204 2 |
| 本文方法 | 0.005 5 | 5.925 8 |
根据图 4可以看出,4种方法均可预测出数据的波动趋势,但是在数值的精度上,本文方法要略优于其它3种方法.从表 1和图 5可以看出,本文方法的MAPE和RMSE都小于其它3种方法,说明本文方法较其它3种方法相比有着良好的精度改善.
5.2 压力超过最低限度的情况下延迟时间的计算本文对压力低于最低安全限度的情况也进行了仿真实验.根据本文的方法取压力自身的延迟时间τ1=10和转炉低压氮气使用流量的延迟时间τ2=6,相关系数方法计算得到τ′1=1和τ′2=1,使用十折交叉验证方法选取LSSVM的参数如表 3所示.
| 预测方法 | 核函数
宽度1 | 核函数
宽度2 | 惩罚系数 |
| 相关系数,原始LSSVM | 4.52 | - | 196.88 |
| Causality,原始LSSVM | 3.87 | - | 210.32 |
| 相关系数,多核LSSVM | 4.02 | 3.87 | 199.74 |
| 本文方法 | 3.16 | 3.53 | 205.13 |
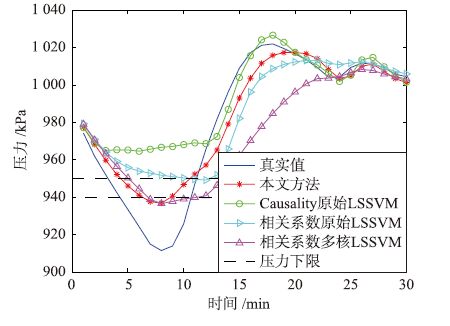
通过本文改进方法与原始LSSVM分别预测,预测结果如图 6所示,误差比较如图 7所示,统计结果如表 4所示.
|
| 图 6 异常工况下预测结果对比 Figure 6 Comparison of the predicted results under the abnormal condition |
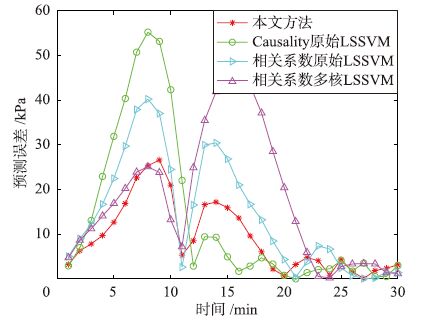
|
| 图 7 异常工况下预测误差对比 Figure 7 Comparison of the predicted errors under the abnormal condition |
| 预测方法 | MAPE | RMSE /kPa |
| 相关系数延迟,原始LSSVM | 0.015 0 | 19.054 5 |
| Causality延迟,原始LSSVM | 0.018 0 | 22.996 2 |
| 相关系数,多核LSSVM | 0.014 3 | 21.941 0 |
| 本文方法 | 0.009 6 | 11.966 6 |
根据图 6可以看出,使用相关系数方法与原始LSSVM进行预测虽然预测出了大致趋势,但是并未预测出压力即将超限的情况.使用基于Causality的方法计算出因素延迟后,直接使用原始LSSVM方法进行预测,效果依然不理想.使用相关系数方法与多核LSSVM预测虽预测出了超限情况,误差却很大,容易引起错误判断.而使用本文方法计算了因素的延迟时间后,通过改进的多核LSSVM方法却准确预测出了压力超限的情况并且在数值上具有较高的精度.从表 4可以看出,本文方法MAPE和RMSE都要小于其它3种方法且RMSE精度提高较大,可信度更高.通过表 2和表 4可以看出,本文方法在正常工况与异常工况下都具有更高的预测精度.
6 结论本文针对冶金企业中的低压氮气系统压力的预测问题进行研究,提出一种基于Causality的影响因素延迟时间计算方法方法,同时根据计算出的二者的延迟时间分别构造训练样本.在预测阶段,本文提出了一种基于影响因素延迟的多核LSSVM模型,用来对低压氮气管网压力进行预测建模.本文通过分别对某冶金企业的低压氮气管网的正常工况和异常工况两种不同的情况进行实验对比,说明本文方法不仅提高了正常生产过程中的预测精度,而且对于管网压力即将发生的异常情况,也给出了较为满意的预测结果,对于低压氮气后续的调度工作具有重要的指导意义.
| [1] | Bhaskar K, Singh S N. AWNN-assisted wind power forecasting using feed-forward neural network[J]. IEEE Transactions on Sustainable Energy, 2012, 3 (2): 306–315. DOI:10.1109/TSTE.2011.2182215 |
| [2] | Zhao J, Wang W, Liu Y, et al. A two-stage online prediction method for a blast furnace gas system and its application[J]. IEEE Transactions on Control Systems Technology, 2011, 19 (3): 507–520. DOI:10.1109/TCST.2010.2051545 |
| [3] | 阎威武, 邵惠鹤. 支持向量机和最小二乘支持向量机的比较及应用研究[J]. 控制与决策, 2003, 18 (3): 358–360. Yan W W, Shao H H. Application of support vector machines and least squares support vector machines to heart disease diagnoses[J]. Control and Decision, 2003, 18 (3): 358–360. |
| [4] | Bouhouche S, Yazid L L, Hocine S, et al. Evaluation using online support-vector-machines and fuzzy reasoning[J]. Control Engineering Practice, 2010, 18 (9): 1060–1068. DOI:10.1016/j.conengprac.2010.05.010 |
| [5] | Carbonneau R, Laframboise K, Vahidov R. Application of machine learning techniques for supply chain demand forecasting[J]. European Journal of Operational Research, 2008, 184 (3): 1140–1154. DOI:10.1016/j.ejor.2006.12.004 |
| [6] | 赵超, 戴坤成. 基于自适应加权最小二乘支持向量机的短期电力负荷预测[J]. 信息与控制, 2015, 44 (5): 634–640. Zhao C, Dai K C. Power system short-term load forecasting based on adaptive weighted least squares support vector machine[J]. Information and Control, 2015, 44 (5): 634–640. |
| [7] | 王通, 高宪文, 翟瑀佳, 等. 基于PSO-LSSVM预测的改进传感器故障检则与隔离[J]. 信息与控制, 2014, 43 (2): 146–151. Wang T, Gao X W, Zhai Y T, et al. Improved detection and isolation of sensor fault based on PSO-LSSVM prediction[J]. Information and Control, 2014, 43 (2): 146–151. |
| [8] | Xi X C, Poo A N, Chou S K. Support vector regression model predictive control on a HVAC plant[J]. Control Engineering Practice, 2007, 15 (8): 897–908. DOI:10.1016/j.conengprac.2006.10.010 |
| [9] | Han Z Y, Liu Y, Zhao J, et al. Real time prediction for converter gas tank levels based on multi-output least square support vector regressor[J]. Control Engineering Practice, 2012, 20 (12): 1400–1409. DOI:10.1016/j.conengprac.2012.08.006 |
| [10] | Zhao J, Liu Y, Zhang X P, et al. A MKL based on-line prediction for gasholder level in steel industry[J]. Control Engineering Practice, 2012, 20 (6): 629–641. DOI:10.1016/j.conengprac.2012.03.003 |
| [11] | Nagai T, Hoshino T, Uchikawa K. Statistical significance testing with Mahalanobis distance for thresholds estimated from constant stimuli method[J]. Seeing and Perceiving, 2011, 24 (2): 91–124. DOI:10.1163/187847511X568180 |
| [12] | Sun H F, Peng Y, Chen J L, et al. A new similarity measure based on adjusted Euclidean distance for memory-based collaborative filtering[J]. Journal of Software, 2011, 6 (6): 993–1000. |
| [13] | Sakurai Y, Papadimitriou S, Faloutsos C. Braid:Stream mining through group lag correlations[C]//Proceedings of the 2005 ACM SIGMOD international conference on Management of data. New York, NJ, USA:ACM, 2005:599-610. |
| [14] | Granger C W J. Investigating causal relations by econometric models and cross-spectral methods[J]. Econometrica:Journal of the Econometric Society, 1969 : 424–438. |
| [15] | Zaremba A, Aste T. Measures of causality in complex datasets with application to financial data[J]. Entropy, 2014, 16 (4): 2309–2349. DOI:10.3390/e16042309 |
| [16] | Kim M. Time-series dimensionality reduction via granger causality[J]. IEEE Signal Processing Letters, 2012, 19 (10): 611–614. DOI:10.1109/LSP.2012.2209641 |
| [17] | Pearl J. Causality:Models, reasoning and inference[M]. Cambridge: MIT Press , 2000 . |
| [18] | Chen F, Zhang D. Combining a causal effect criterion for evaluation of facial attractiveness models[J]. Neurocomputing, 2015 . |
| [19] | Zhang Q, Dong C L, Cui Y, et al. Dynamic uncertain causality graph for knowledge representation and probabilistic reasoning:Statistics base, matrix, and application[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25 (4): 645–663. DOI:10.1109/TNNLS.2013.2279320 |
| [20] | Dai H, Keble-Johnston S, Gan M. Reliable knowledge discovery with a minimal causal model inducer[C]//IEEE 12th International Conference on Data Mining Workshops (ICDMW). Piscataway, NJ, USA:IEEE, 2012:629-634. |
| [21] | Wang C. Hybrid causal models for system diagnostics[C]//2011 Proceedings of Annual IEEE Reliability and Maintainability Symposium (RAMS). Piscataway, NJ, USA:IEEE, 2011:1-4. |
| [22] | Liu Y, Gao Z L, Li P, Wang H Q. Just-in-time kernel learning with adaptive parameter selection for soft sensor modeling of batch processes[J]. Industrial & Engineering Chemistry Research, 2012, 51 (11): 4313–4327. |



