UAV 3D Path Planning and Obstacle Avoidance Method
-
摘要:
针对无人机（UAV）在三维环境中如何由起始点到目标点合理地规划路径避开障碍物，提出了一种基于改进粒子群算法与滚动策略相结合的UAV路径规划与避障方法.该方法首先以UAV为中心，通过传感器建立UAV的可视区域模型；其次结合滚动策略滚动探知UAV周围环境信息；最后，利用改进的粒子群算法进行路径搜索，并加入综合转角控制提高路径的平滑性.在传统粒子群算法中加入信息素与启发函数，增强算法的全局搜索能力，并对参数进行特定设计提高算法的收敛速度.仿真结果表明，该方法可以实现实时避障，所规划的路径相对平滑，且改进算法比传统算法具有较高的收敛性.
Abstract:We address the problem of how UAVs in the three-dimensional environment can reasonably plan a path that avoids obstacles from the starting point to a target point. UAV path planning and obstacle avoidance method are proposed, based on the combination of improved particle swarm optimization and rolling strategy methods. First, the proposed method uses the UAV as the center and uses sensors to establish a UAV visual area model.Next, scrolling strategies are combined to obtain information about the environment surrounding the UAV.Lastly, the improved particle swarm algorithm is used to search the path, with the addition of integrated corner control to improve path smoothness. Pheromone and heuristic functions are added to the traditional particle swarm optimization algorithm to enhance the algorithm's global search capability, and the parameters are specifically designed to improve the algorithm's convergence speed. Simulation results show that the proposed method can achieve real-time obstacle avoidance, the planned path is relatively smooth, and the improved algorithm has higher convergence than the traditional algorithm.
-
0. 引言
近几年，由于无人机(UAV)体积小、运动速度快、代价低，在电力巡线中的应用越来越多. 无人机进行电力巡线时在满足约束的条件下如何由起点到任务点，避开障碍成为现阶段无人机巡线应用中比较重要的问题之一[1].
UAV路径规划是指在考虑地形、环境等因素的前提下，根据UAV的能耗、速度、体型设计出满足UAV最优性能的路径. 文[2]中，考虑山峰的密集度，根据山峰位置建立泰森多边形，提出一种基于改进蚁群算法的UAV路径规划方法，可为UAV规划出较短路径，但是该方法未考虑出现动态障碍物的情况. 文[3]中，通过设计多层扩展A*算法，提出了一种在复杂环境下无人机的路径规划方法，可在考虑路径平滑性的前提下快速规划出一条路径，但该方法规划时间较长；文[4]中，提出一种通过生物神经动力学模型来解决UAV三维空间的路径规划问题，并能解决UAV的实时避障问题，但该方法不能达到全局最优. 关于路径规划算法，现在主要有蚁群算法、神经网络算法、粒子群算法以及一些改进的智能算法[5-7]. 传统算法虽然对目标及约束定义明确，但是收敛速度慢、容易陷入局部，其借鉴意义不大. 由于粒子群算法速度快，易于实现，因此在路径规划中受到广泛应用. 文[8]中，在粒子群算法中引入自然选择系数和惯性权重，极大地提高了粒子群算法的收敛性，解决了算法易陷入局部最优的问题，同时缩短了路径长度. 文[9]中，通过交叉变异、惯性调节参数并用元矩阵定义离散粒子的方式来使粒子保持多样性，解决了自主水下航行器的侦察问题. 文[10]中，提出了一种改进的粒子群算法，该算法由随机期望值决定速度更新模型，通过在速度更新方程中增加随机时滞，避免粒子群算法陷入局部.
综合上述分析，本文提出一种基于改进粒子群算法与滚动策略相结合的UAV路径规划与避障方法. 该方法由传感器半径R为边界，UAV中心为球心，建立10个等间距的同心球体，结合滚动策略实时探知UAV周围环境，通过改进的粒子群算法为UAV规划路径，解决了以往路径规划不能在动态环境中应用的问题. 通过该方法可以使UAV快速准确地探知到其周围的环境信息并可避免随机产生的威胁，为UAV的路径规划提供准确的环境信息；在算法中引入信息素，通过为每个粒子加载信息素提高算法的收敛速度，通过加入启发函数增强粒子对下一目标点选择的目的性提高全局搜索能力，算法参数的选择对于粒子群算法的性能起到重要的作用[11]，本文通过对参数分析、计算选出了最优的参数.
1. UAV三维空间模型
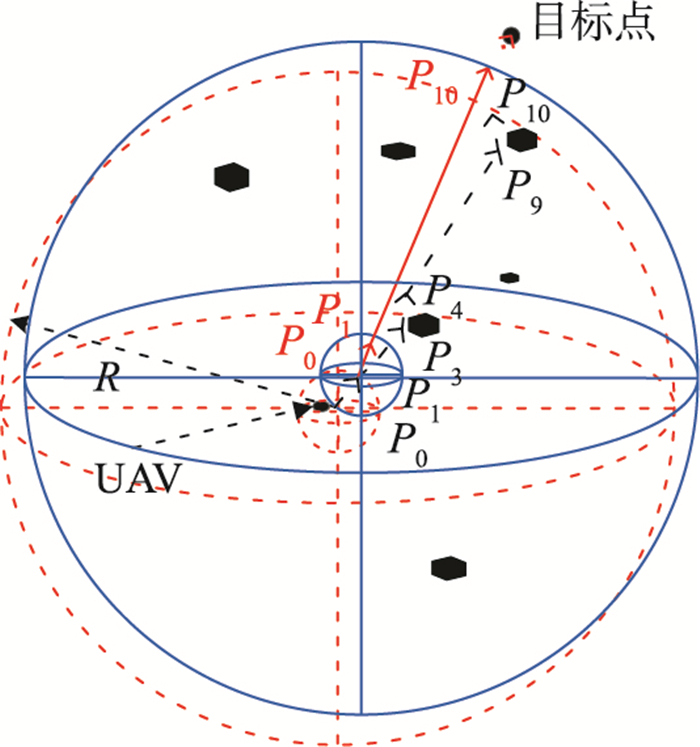
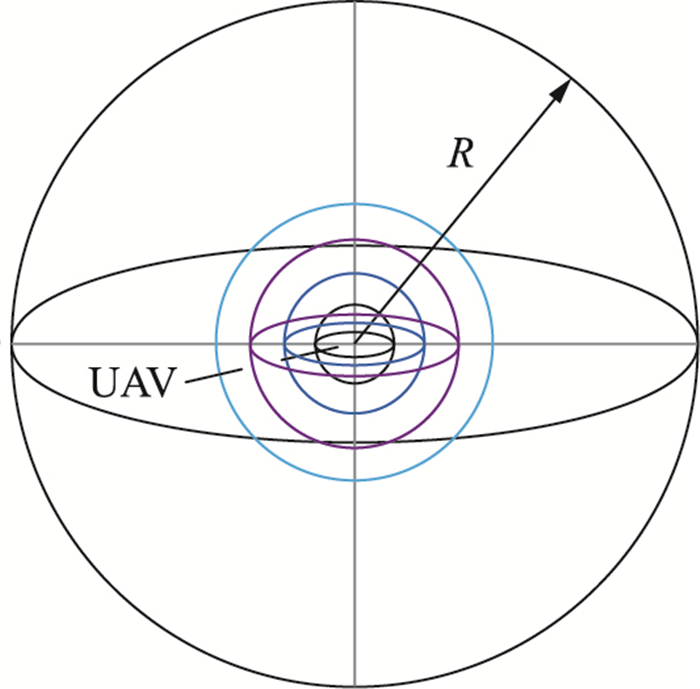
UAV装有传感器探知周围的环境信息，传感器的探知半径为R. 在UAV工作的三维环境中，以UAV的中点为球心等间距地分布着10个三维球体模型，如图 1所示. 与UAV相邻的同心球体上存在UAV下一飞行的子目标点. UAV通过滚动的方式对比个体最短子路径和最优综合转向角来规划最优路径.
2. 滚动策略研究
UAV通过传感器以自身中心为球心探知周围半径为R的区域内的环境信息，该区域为UAV的可视区域. 如图 2所示，长方体为UAV探知的障碍物. UAV的可视区域为一个滚动窗口，如图 2虚线球体所示，UAV在当前位置P分别以0.1R，0.2R，0.3R，…，0.9R，R为半径产生10个同心球体. 在10个同心球体上分布着n个随机节点，UAV从这些节点中选取代价最小的节点来组成UAV的子路径. 这样在10个同心圆上就产生了10个随机的点(P1，P2，…，P10)，图 2中黑虚线为这几点的连接线，即UAV的子路径. 当UAV到达P1点时，产生新的10个同心球体，如图 2中实线球体所示，图中红实线为规划的新一轮的子路径. 以此类推，直到到达目标点为止.
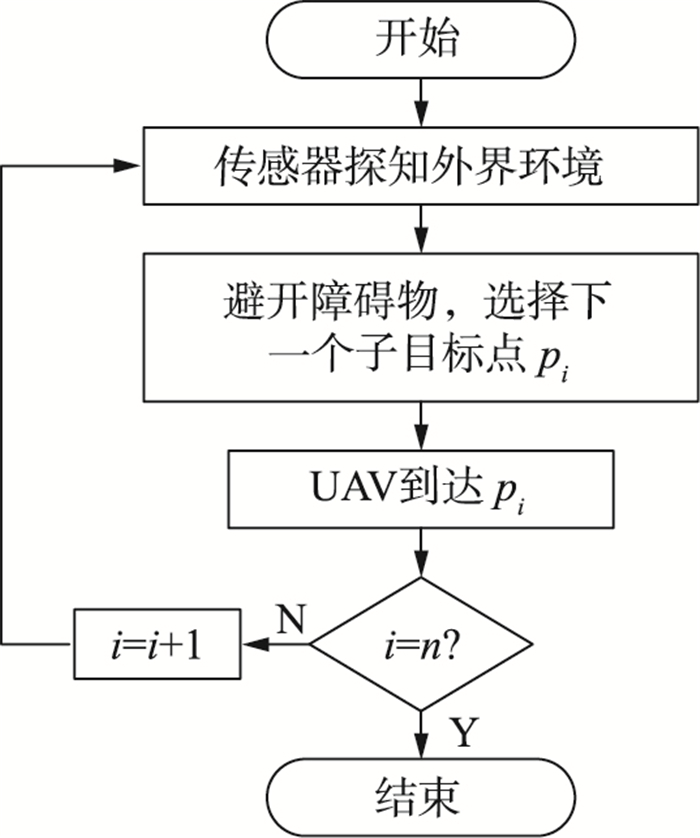
具体运行步骤如下：
步骤1：UAV通过传感器获得可视区域内的环境信息.
步骤2：通过传感器探知的环境信息，UAV在避开障碍物的前提下，规划出一条最优子路径.
步骤3：UAV沿步骤2路径飞行到下一点，以该点为中心更新滚动窗口.
步骤4：当UAV到达位置Pi+1时，i=i+1，并返回步骤1，直到UAV行驶到目标点.
3. UAV路径规划算法研究
传统粒子群算法是一种随机寻优算法，其实质是各粒子之间相互分享信息，群体综合各个粒子的信息比较分析选择出最优解. 在早期传统粒子群算法相较于其他智能算法容易实现、优化效果好、速度较快，在路径规划中有大量运用[12]. 后来学者发现传统的粒子群算法收敛速度慢、全局规划能力差，对其的应用越来越少[13].
本文考虑了传统粒子群算法的以上缺点，对算法进行了优化设计.
3.1 粒子群优化算法设计
本文中UAV处在三维环境中，所以UAV的维度系数d为3. 粒子的更新机制以及对自身的评价基于单个粒子寻找到的最优路径(单个极值)和粒子群整体寻找到的最优路径(群体极值). 粒子的优劣性通过最优路径和最小综合转向角来判断. 为了避免粒子陷入局部最优本文加入信息数浓度函数与启发函数来改进粒子群算法[14]. 粒子的自我更新为
(1) 
(2) 式中，vidt为第i个粒子在d维度第t次迭代时的速度；sidt为粒子第t次迭代时的位置；c1，c2为学习因子；r1，r2取[0, 1]之间的随机数；ω为惯性权重；ppbt为第t次迭代后个体最优值；pgbt为第t次迭代后种群最优值；Pidt为粒子选择下一点的概率.
节点选择概率为
(3) 式中，τidt(x，y，z)表示信息素浓度，Qidt(x，y，z)表示在t次迭代时的启发函数.
3.2 适应度函数的选取
粒子群算法是通过不断迭代在各个随机解中选择出最适合的解值，适应度函数用来评价解的优劣性. 当UAV从起始点到目标点时，除了UAV的飞行路径对能耗有影响之外，UAV在转向时也消耗能量. 故本文考虑的适应度函数有两方面：1) UAV起始点到目标点的路径最短. 2) UAV的综合转向角最小. 适应度函数的选取是为了在粒子群优化算法的不断迭代中找出可以适应度函数值最小的解. 综合以上考虑，本文选取适应度函数为上述两者之和. 这样既考虑到了UAV的飞行路径，同时又使得UAV飞行更为平滑.
假设UAV的起始点位置为(x0，y0，z0)，局部目标点位置为(x9，y9，z9)，途径的子目标点位置为(xi，yi，zi)，其中i=0，1，2，…，9. 则适应度函数f1为
(4) 由以上分析可知，除了考虑UAV的飞行路径最短之外，还应考虑UAV的综合转向角最小，使UAV的飞行路径更为平滑. 则适应度函数f2为
(5) 综合以上考虑，UAV的适应度函数f为
(6) 为了使无人机可以在自身飞行距离内完成工作并安全返回基地，每次规划的路径长度应在一定范围之内：
(7) 式中，0.1 < β < 0.25表示路径系数；L为无人机续航距离；B为无人机理想路径长度.
3.3 信息素浓度
信息素浓度为蚁群算法中为了避免陷入局部最优而设立的一个函数，本文将信息素浓度融入粒子群算法以增加粒子群算法的全局可靠性[15-16]. 通过对每个粒子加载信息素提高算法的收敛速度.
局部信息素浓度更新公式：
(8) 式中，τidt(x，y，z)为第t次迭代式信息素浓度，τidt+1(x，y，z)第t+1次迭代式信息素浓度；0 < ξ < 1为衰减系数.
全局信息素浓度更新公式为
(9) 式中，η为信息更新系数.
(10) 式中，tmax为最大迭代次数；t为当前迭代次数；l(a)为第a个粒子的路径规划长度. 全局信息素的更新可避免算法后期信息素的变化缓慢.
3.4 启发函数
通过加入启发函数来增强粒子对下一节点选择的目的性. 启发函数如下：
(11) 式中，D1(x，y，z)表示粒子从当前位置到下一位置的距离，D2(x，y，z)表示粒子由下一位置到目标点的距离；Tidt(x，y，z) 表示路径的威胁系数(有无障碍物).
(12) 
(13) 
(14) 3.5 参数设置
粒子的上一代速度对下一代速度存在着一定的影响，此影响由ω决定，同时它还对粒子的全局搜索能力与局部搜索能力有影响[17]. 随着ω的增大，粒子的全局搜索能力增强并且算法收敛性也越好，但不易获得问题的最优解；当ω变小时，粒子的局部搜索能力增强，问题的最优解容易获得，但算法的收敛性变差，甚至停止[18-19]. 因此需要确定合适的ω提高算法的收敛速度与稳定性. ω与迭代次数的关系是负相关的[20].
(15) 式中，α=π/4，ωs=0.9，表示ω的最大值；ωe=0.4，表示ω的最小值；m=0.5，表示控制因子.
学习因子同样影响粒子的下一代速度[21]. 在算法的早期进行时，更注重粒子的全局搜索能力；在算法后期更加注重局部搜索能力[22]. 迭代次数与学习因子的关系式如下：
(16) 式中，c1s=c2e=2.5；c1e=c2s=1.0. 随着迭代次数的增加a1由1.0到2.5非线性变化，a2由2.5到1.0非线性变化.
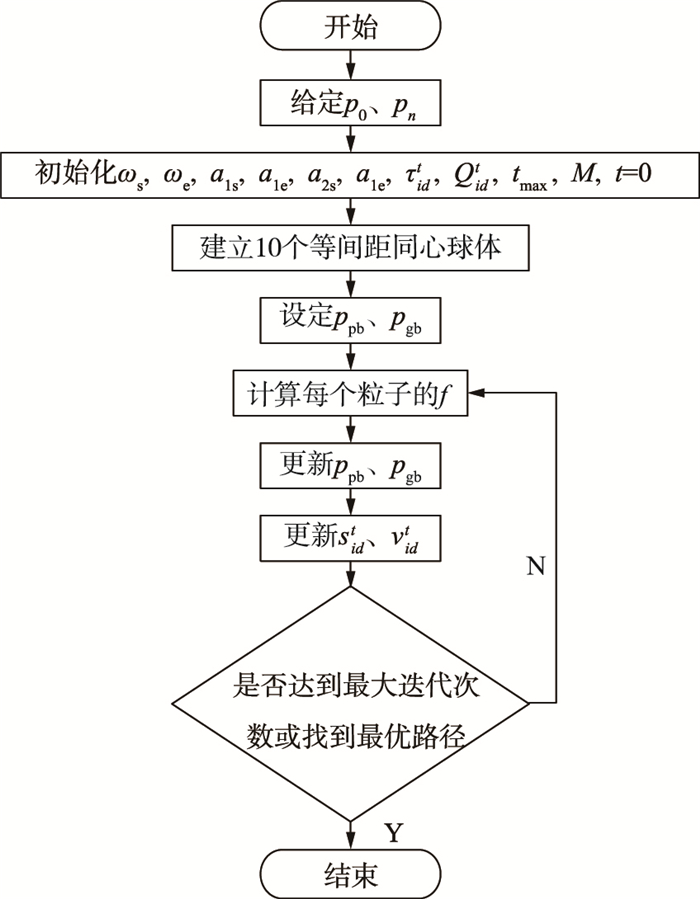
算法步骤如下：
步骤1：给定UAV的起止点与目标点.
步骤2：初始化参数：ωs、ωe、a1s、a1e、a2s、a2e，τidt，Qidt，tmax，t=0，种群数量M.
步骤3：以UAV当前位置为圆心，在传感器探知范围内，设立10个等间距的同心圆.
步骤4：设定粒子个体历史最优值ppb和种群历史最优解pgb；
步骤5：计算每个粒子的适应度值f.
步骤6：更新ppb和pgb.
步骤7：更新粒子的速度和位置.
步骤8：找到本次最优路径，输出gbest. 否则，重复步骤5.
4. 仿真验证
本文基于Matlab仿真平台，分析了UAV在静态与动态下滚动策略路径规划的可行性与UAV综合转向角的平滑性，并与传统粒子群算法进行比较.
4.1 路径规划可行性仿真
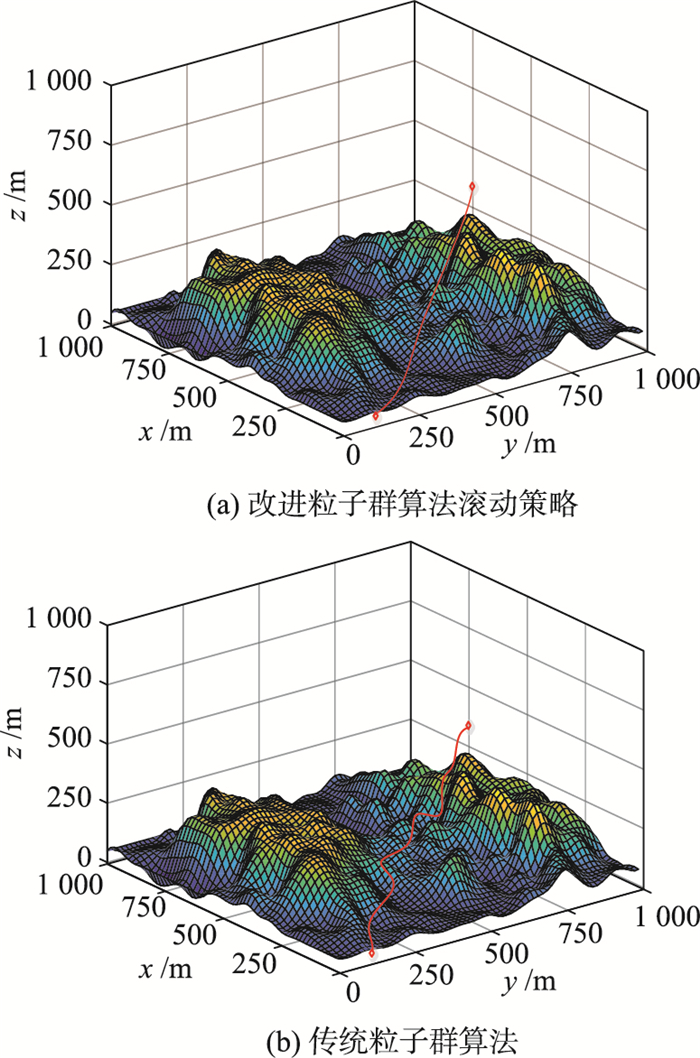
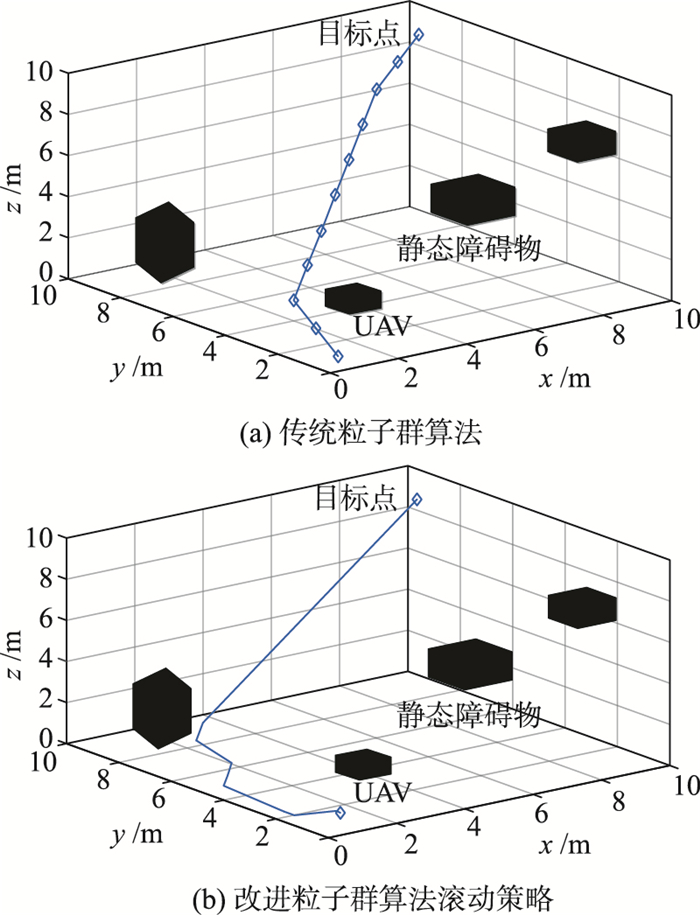
本节在1 000 m×1 000 m的区域内对本方法进行可行性仿真验证. 种群数量为80，最大迭代次数为180. 仿真结果如图 5所示. 从图 5中可以看出，应用传统粒子群算法规划出的路线转向较多，路径较长，这是因为其所规划的路线只考虑局部没有考虑UAV整体路径的平滑性. 由于本文提出的方法在传统粒子群算法中加入启发函数与信息数并对参数进行的特定设置可以避免算法陷入局部最优，故可以规划出更短且更平滑的路线.
4.2 路径规划性能分析
本节对各参数进行适量缩小，具体分析本方法路径规划的性能.
表 1 仿真环境表Tab. 1. Simulation environment数值 UAV速度V 0.01 m/s~0.05 m/s 传感器探知半径R 1 m 同心球体等值间距 0.1 m UAV起始点与目标点的距离 14 m UAV最大转向步数 100 最大迭代次数N 180 种群规模M 80 4.2.1 静态路径规划
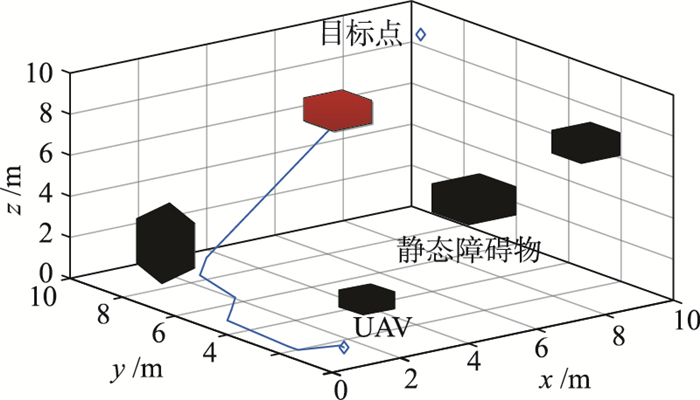
本节讨论UAV在静态环境下的路径规划问题. 仿真结果如图 6所示.
从图 6(a)中可以看出，应用传统的粒子群算法，当UAV开始运动时，由于探知到周围没有障碍物，UAV开始随意运动，并且出现了反向运动. 这样不仅增加了UAV的能耗且使得UAV到达目标点的时间变长. 当传感器探知到周围有障碍物时，由于传统的粒子群算法，将UAV看做一个质点，没有考虑UAV的安全飞行距离，使得UAV有撞向障碍物的风险. 从图 6(b)可以看出，使用本文提出的改进粒子群算法，当UAV开始运动时，即使没有探知到附近有障碍物，UAV仍然会选择路径最优的路线继续飞行. 当传感器探测到周围有障碍物时，由于提前设定了UAV的安全飞行距离，并且UAV临近球体上所有的点都是UAV下一个潜在子目标点，使得UAV永远可以选择最安全并且路径最合适的点作为下一子目标点. UAV在不断选择最优区域路径时，逐渐到达设定目标点. 通过仿真可知，用本文所提出的改进粒子群算法对UAV进行路径规划及避障是可行、高效的.
4.2.2 动态路径规划
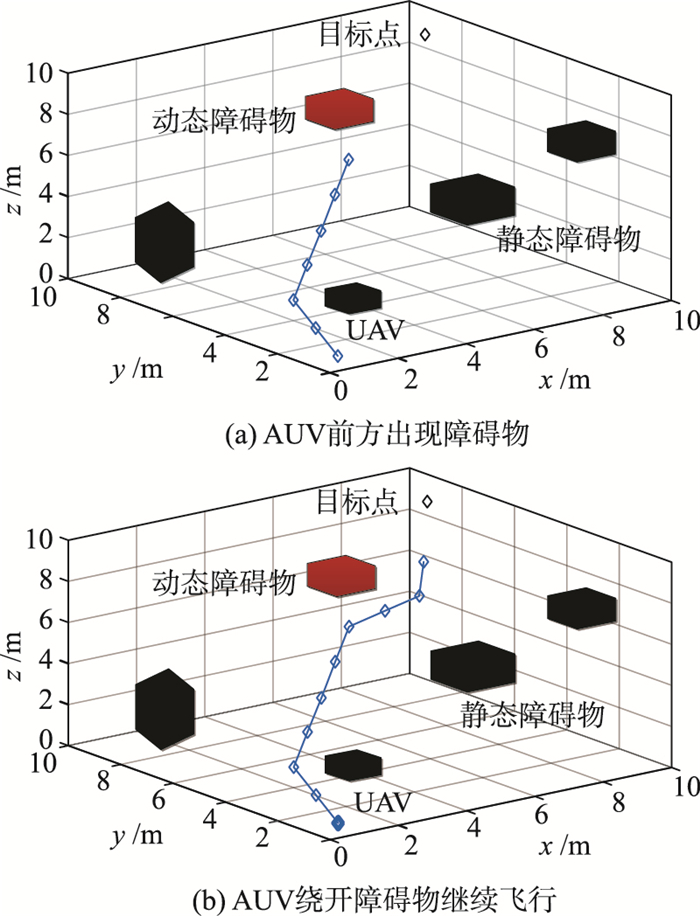
UAV在实际工作中，由于其工作环境的不确定性在其飞行路线上可能会出现动态障碍物. 本节讨论UAV在动态环境下的路径规划与避障. 仿真结果图 7、图 8所示.
![]()
图 7 传统粒子群算法动态环境路径规划Fig. 7. Traditional particle swarm optimization dynamic environment path planning![]()
图 8 改进粒子群优化算法滚动策略动态环境路径规划Fig. 8. Improved PSO (particle swarm optimization) rolling strategy dynamicenvironment path planning从图 7中可以看出，当UAV前方出现障碍物时，由于传统的方法不能及时搜索发现障碍物，使得UAV撞上了障碍物. 在图 8(a)中，UAV飞行的前方出现方形障碍物，此时，传感器以滚动的方式实时探知周围的障碍物，并且将障碍物的信息传递给UAV，重新规划UAV的飞行路径. 如图 8(b)所示，重新规划的飞行路径成功地避开了障碍物. 由于本文采用滚动策略来探知UAV周围的环境情况，当突然出现动态的障碍物时，本方法也可以实时检测到并且避开障碍物为UAV规划出合理的路线.
4.3 路径平滑性分析
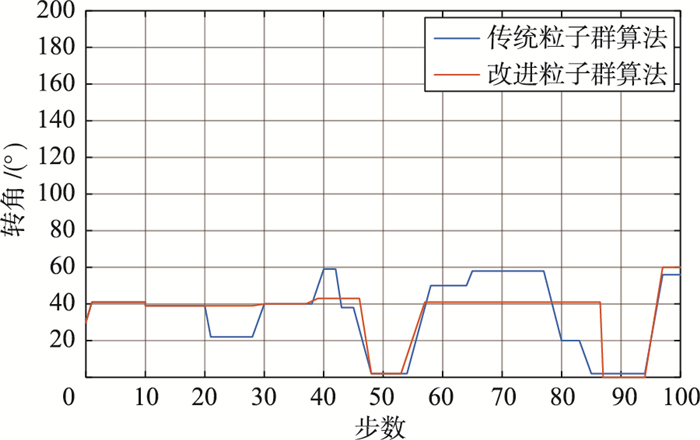
本节对两种算法规划的路径进行综合转向角的平滑性对比. 仿真结果如图 9所示.
从图 9中可以看出，UAV在改进粒子群算法规划的路径中要比传统粒子群算法转角的次数少很多，说明应用改进的粒子群算法可以提高路径的平滑性.
4.4 收敛性对比
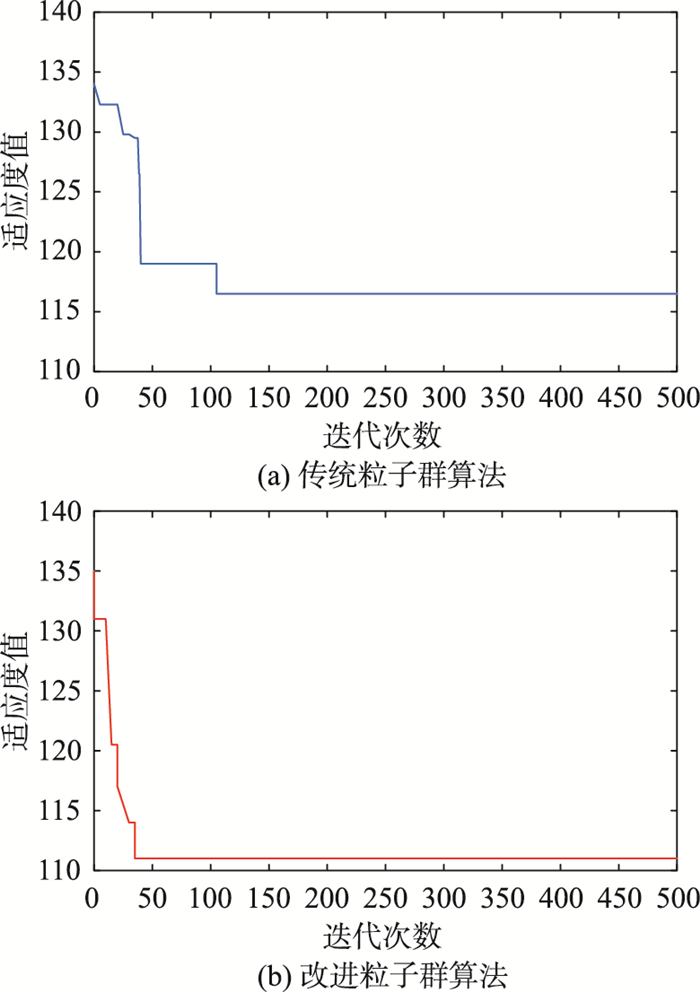
本节讨论传统粒子群算法与本文改进粒子群算法的收敛性，两种算法的适应度值曲线如图 10所示.
从图 10中可以看出，改进粒子群算法比传统粒子群算法收敛更快. 传统的粒子群算法在102次迭代中陷入了局部最优，改进的粒子群算法相较于传统粒子群算法在局部最优的问题上的得到了改进，不易陷入局部最优. 两种算法的对比见表 2.
表 2 迭代次数对比表Tab. 2. Comparison of iteration times算法 稳定时的迭代次数 稳定时的适应度值 传统粒子群算法 102 116 改进粒子群算法 41 111 通过多次的仿真比较，滚动策略结合改进粒子群算法的路径规划方法在路径规划曲线上优于传统的例子群算法，且改进粒子群算法比传统粒子群算法收敛速度更快，不易陷入局部最优.
5. 结论
本文提出了一种滚动策略实时探知UAV周围的环境情况，并与粒子群算法相结合对UAV进行路径规划和避障的方法. 该方法通过UAV自身携带的传感器建立三维模型，传感器在三维模型内运用滚动的模式来实时探知UAV周围的环境情况，为UAV规划路线. 本文在静态环境与动态环境下对本方法进行仿真验证，并与传统的粒子群算法进行比较证明了本方法的可行性与高效性且证明了此方法规划的路径平滑性更好. 在与传统粒子群算法关于收敛性的对比中，本文提出的改进算法也表现出了较高的收敛性.
-
![]()
图 4 改进粒子群优化算法流程图
Figure 4. Flowchart of improved particle swarm optimization algorithm
![]()
图 7 传统粒子群算法动态环境路径规划
Figure 7. Traditional particle swarm optimization dynamic environment path planning
![]()
图 8 改进粒子群优化算法滚动策略动态环境路径规划
Figure 8. Improved PSO (particle swarm optimization) rolling strategy dynamicenvironment path planning
表 1 仿真环境表
Table 1 Simulation environment
数值 UAV速度V 0.01 m/s~0.05 m/s 传感器探知半径R 1 m 同心球体等值间距 0.1 m UAV起始点与目标点的距离 14 m UAV最大转向步数 100 最大迭代次数N 180 种群规模M 80 
下载: 导出CSV
表 2 迭代次数对比表
Table 2 Comparison of iteration times
算法 稳定时的迭代次数 稳定时的适应度值 传统粒子群算法 102 116 改进粒子群算法 41 111
下载: 导出CSV
-
[1] 施孟佶, 秦开宇, 李凯, 等. 高压输电线路多无人机自主协同巡线设计与测试[J]. 电力系统自动化, 2017, 41(10): 117-122. https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT201710017.htm Shi M J, Qin K Y, Li K, et al. Design and test of multi UAV autonomous cooperative line patrol for high voltage transmission lines[J]. Power System Automation, 2017, 41(10): 117-122. https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT201710017.htm
[2] 唐立, 郝鹏, 张学军. 基于改进蚁群算法的山区无人机路径规划方法[J]. 交通运输系统工程与信息, 2019, 19(1): 158-164. https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201901025.htm Tang L, Hao P, Zhang X J. Path planning method of UAV in mountain area based on improved ant colony algorithm[J]. Transportation System Engineering and Information, 2019, 19(1): 158-164 https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201901025.htm
[3] 谭雁英, 李洋, 周军, 等. 复杂环境下基于A*算法的无人机路径再规划[J]. 系统工程与电子技术, 2017, 39(6): 1268-1273. https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD201706013.htm Tan Y Y, Li Y, Zhou J, et al. Path re planning of UAV Based on A* algorithm in complex environment[J]. System Engineering and Electronic Technology, 2017, 39(6): 1268-1273. https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD201706013.htm
[4] Li S, Guo Y. Neural-network based AUV path planning in estuary environments[C]//Proceedings of the 10th World Congress on Intelligent Control and Automation, Piscataway, NJ, USA: IEEE, 2012: 3724-3730.
[5] WU Q, Lin H, Jin Y Z. A new fallback beetle antennae search algorithm for path planning of mobile robots with collision-free capability[J]. Soft Computing, 2020, 24(3): 2369-2380. doi: 10.1007/s00500-019-04067-3
[6] Mohammadreza R, Manish K, Alireza N, et al. Dynamic optimal UAV trajectory planning in the national airspace system via mixed integer linear programming[J]. Proceedings of the Institution of Mechanical Engineering. DOI: 10.13140/RG.2.1.1157.9608.
[7] 练青坡, 王宏健, 袁建亚, 等. 基于粒子群优化算法的USV集群协同避碰方法[J]. 系统工程与电子技术, 2019, 41(9): 2034-2040. https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD201909016.htm Lian Q P, Wang H J, Yuan J Y, et al. USV cluster collaborative collision avoidance method based on particle swarm optimization algorithm[J]. System Engineering and Electronic Technology, 2019, 41(9): 2034-2040. https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD201909016.htm
[8] 张建南, 刘以安, 王刚. 基于优化粒子群算法的无人机航路规划[J]. 传感器与微系统, 2017, 36(3): 58-61. https://www.cnki.com.cn/Article/CJFDTOTAL-CGQJ201703016.htm Zhang J N, Liu Y A, Wang G. Route planning of UAV based on particle swarm optimization algorithm[J]. Sensors and Microsystems, 2017, 36(3): 58-61 https://www.cnki.com.cn/Article/CJFDTOTAL-CGQJ201703016.htm
[9] Zhang Y Z. An improved PSO algorithm for solving multi-UAV cooperative reconnaissance task decision-making problem[C]//Proceedings of 2016 IEEE/CSAA International Conference on Aircraft Utility Systems. Piscataway, NJ, USA: IEEE, 2016: 434-437.
[10] 王闯, 董宏丽, 谷星澍, 等. 改进粒子群算法及其在航迹规划中的应用[J]. 控制工程, 2019, 26(8): 1466-1471. https://www.cnki.com.cn/Article/CJFDTOTAL-JZDF201908006.htm Wang C, Dong H L, Gu X S, et al. Improved particle swarm optimization and its application in track planning[J]. Control Engineering, 2019, 26(8): 1466-1471. https://www.cnki.com.cn/Article/CJFDTOTAL-JZDF201908006.htm
[11] Mandavark B. An optimized path planning for the mobile robot using potential field method and PSO algorithm[J]. Intelligent System and Computing, 2019, 10(817): 139-150. http://www.researchgate.net/publication/328640312_An_Optimized_Path_Planning_for_the_Mobile_Robot_Using_Potential_Field_Method_and_PSO_Algorithm_SocProS_2017_Volume_2
[12] 胡小宇, 刘庆, 贺文宁, 等. 基于粒子群算法的单仓储多车物流配送优化[J]. 计算机应用, 2018, 38(S2): 21-26. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY2018S2005.htm Hu X Y, Liu Q, He W N, et al. Optimization of single warehouse storage and multi vehicle logistics distribution based on particle swarm optimization[J]. Computer Application, 2018, 38(S2): 21-26. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY2018S2005.htm
[13] 王雷震, 汪定伟, 王素欣. 多起讫点货物转运配送车辆调度模型及其粒子群、蚁群算法混合求解[J]. 信息与控制, 2018, 47(5): 564-572. doi: 10.13976/j.cnki.xk.2018.7037 Wang L Z, Wang D W, Wang S X. Vehicle scheduling model and hybrid solution of particle swarm optimization and ant colony algorithm for multi origin and destination goods transfer and distribution[J]. Information and Control, 2018, 47(5): 564-572. doi: 10.13976/j.cnki.xk.2018.7037
[14] 许凯波, 鲁海燕, 黄洋, 等. 基于双层蚁群算法和动态环境的机器人路径规划方法[J]. 电子学报, 2019, 47(10): 2166-2176. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXU201910019.htm Xu K B, Lu H Y, Huang Y, et al. Robot path planning method based on two-layer ant colony algorithm and dynamic environment[J]. Journal of Electronics, 2019, 47(10): 2166-2176. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXU201910019.htm
[15] 裴振兵, 陈雪波. 改进蚁群算法及在车辆运输调度中的应用[J]. 信息与控制, 2015, 44(6): 753-758. https://www.cnki.com.cn/Article/CJFDTOTAL-XXYK201506019.htm Pei Z B, Chen X B. Improved ant colony algorithm and its application in vehicle transportation scheduling[J]. Information and Control, 2015, 44(6): 753-758. https://www.cnki.com.cn/Article/CJFDTOTAL-XXYK201506019.htm
[16] Takitou S, Taneda A. Ant colony optimization for predicting RNA folding pathways[J]. Computational Biology and Chemistry, 2019. DOI: 10.1016/j.compbiolchem.2019.107118.
[17] Jiang J, Han F, Ling Q H, et al. Efficient network architecture search via multiobjective particle swarm optimization based on decomposition[J]. Neural Networks: The Official Journal of the International Neural Network Society, 2020, 123: 305-316. doi: 10.1016/j.neunet.2019.12.005
[18] Chen R M, Shen Y M, Hong W Z. Neural-like encoding particle swarm optimization for periodic vehicle routing problems[J]. Expert Systems with Applications, 2019. DOI: 10.1016/j.eswa.2019.112833.
[19] 李荣雨, 周志勇. 成长性的粒子群算法及其在函数优化中的应用[J]. 信息与控制, 2017, 46(2): 224-230. doi: 10.13976/j.cnki.xk.2017.0224 Li R Y, Zhou Z Y. Growing particle swarm optimization and its application in function optimization[J]. Information and Control, 2017, 46(2): 224-230. doi: 10.13976/j.cnki.xk.2017.0224
[20] 张少明, 盛四清. 基于改进粒子群算法的微网优化运行[J]. 中国电力, 2020, 53(5): 24-31. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDL202005004.htm Zhang S M, Sheng S Q. Microgrid optimization operation based on improved particle swarm optimization algorithm[J]. China Power, 2020, 53(5): 24-31. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDL202005004.htm
[21] 徐利锋, 黄祖胜, 杨中柱, 等. 引入多级扰动的混合型粒子群优化算法[J]. 软件学报, 2019, 30(6): 1835-1852. https://www.cnki.com.cn/Article/CJFDTOTAL-RJXB201906018.htm Xu L F, Huang Z S, Yang Z Z, et al. Hybrid particle swarm optimization algorithm with multi-level disturbance[J]. Journal of Software, 2019, 30(6): 1835-1852. https://www.cnki.com.cn/Article/CJFDTOTAL-RJXB201906018.htm
[22] Su S J, Han J, Xiong Y P. Optimization of unmanned ship's parametric subdivision based on improved multi-objective PSO[J]. Ocean Engineering, 2019, 194: 1-12.
-
期刊类型引用(22)
1. 丁兵兵，匡珍春，卢来. 基于Q学习算术优化算法的无人机三维航迹规划. 电光与控制. 2024(03): 61-69 . 
百度学术
2. 侯晨曦. 基于滚动速度障碍法的无人机山地航测避障路径规划研究. 计算机测量与控制. 2024(03): 232-238+246 . 百度学术
3. 褚宏悦，易军凯. 无人机安全路径规划的混沌粒子群优化研究. 控制工程. 2024(06): 1027-1034 . 百度学术
4. 陈福金. 基于CLGWO的无人机三维路径规划研究. 经纬天地. 2024(03): 77-82 . 百度学术
5. 朱孝山，刘伟伟. 融合多策略改进黑猩猩优化算法的UAV航迹规划. 电光与控制. 2024(08): 50-57+68 . 百度学术
6. 蒲兴成，汪欢，谭令，陈雨柔，王淑真. 基于自适应动态窗口改进细菌趋化算法的UAV三维路径规划. 徐州工程学院学报(自然科学版). 2024(03): 40-53 . 百度学术
7. 张颖，姜文刚，陈一鸣，管文瑞. 基于改进蜘蛛蜂算法的无人机三维路径规划. 电子测量技术. 2024(11): 101-111 . 百度学术
8. 王智慧，代永强，刘欢. 基于自适应飞蛾扑火优化算法的三维路径规划. 计算机应用研究. 2023(01): 63-69 . 百度学术
9. 路世昌，邵旭伦，李丹. 卡车-无人机协同救灾物资避障配送问题研究. 计算机工程与应用. 2023(02): 289-298 . 百度学术
10. 胡观凯，钟建华，李永正，黎万洪. 基于IPSO-GA算法的无人机三维路径规划. 现代电子技术. 2023(07): 115-120 . 百度学术
11. 陈超，段纳，徐止政. 具有输入死区与扰动的四旋翼无人机自抗扰控制. 信息与控制. 2023(03): 326-333 . 本站查看
12. 刘继新，蒋伶潇，刘禹汐，张新珏. 无人机冲突探测与解脱技术研究概述. 科学技术与工程. 2023(26): 11081-11089 . 百度学术
13. 刘开芬，冯烨，张飞霞，陈晔. 一种多无人机分布式路径规划算法. 电讯技术. 2023(10): 1507-1514 . 百度学术
14. 黄志锋，刘媛华. 基于改进狮群算法的城市无人机低空路径规划. 信息与控制. 2023(06): 747-757+772 . 本站查看
15. 骆海涛，孙嘉泽，高鹏宇，曾德生，李家成. 基于改进RRT~*算法的智能轮椅全局路径规划研究. 仪器仪表学报. 2023(10): 303-313 . 百度学术
16. 潘楠，张淼寒，韩宇航，向泓宇，刘海石，殷实，潘地林. 面向城市巡防的多无人机协同航迹规划. 信息与控制. 2022(04): 411-422 . 本站查看
17. 辛守庭，赵冠宇，王晓光，谷海红. 基于改进粒子群算法的旋翼无人机三维航迹规划. 飞行力学. 2022(05): 47-52+73 . 百度学术
18. 赵其定，汪夏荣. 无人机覆盖路径规划中基于能量感知网格的三维避障算法的研究. 现代信息科技. 2022(18): 75-80 . 百度学术
19. 冒燕，杨家鼎，徐小强. 基于改进速度障碍算法的无人机反侦察路径规划研究. 弹箭与制导学报. 2022(06): 13-19 . 百度学术
20. 贺娇，谭代伦. 基于视野范围和遗传算法的三维地形路径规划. 计算机工程与应用. 2021(15): 279-285 . 百度学术
21. 彭育辉，江铭，马中原，钟聪. 汽车自动驾驶关键技术研究进展. 福州大学学报(自然科学版). 2021(05): 691-703 . 百度学术
22. 齐永波. 实景三维技术在地质勘查工作中的应用研究. 测绘与空间地理信息. 2021(11): 206-208+212 . 百度学术
其他类型引用(21)
计量
- 文章访问数: 665
- HTML全文浏览量: 15
- PDF下载量: 664
- 被引次数: 43
