Quantum Zero-watermark Algorithm Based on Quantum Information Processing
-
摘要:
基于量子信息处理提出了一种量子音频的零水印算法.首先利用量子离散余弦变换在宿主量子音频频域内的低频区域提取一组量子序列，然后利用Henon映射对该序列执行加密算法，从而生成量子零水印.通过将Henon映射的量子线路作为零水印的量子秘钥，有效地提高了量子零水印算法的安全性.本文设计了量子Henon映射置乱和量子零水印生成及提取算法的线路图，对零水印算法的可行性进行了验证.仿真实验表明，与现有的量子音频水印算法相比，本文提出的量子零水印算法具有更好的不可感知性及鲁棒性.
-
关键词:
- 量子信息处理 /
- 量子离散余弦变换 /
- 量子Henon映射加密 /
- 量子零水印
Abstract:Based on quantum information processing, a zero watermarking algorithm for quantum audio is proposed. Firstly, a set of quantum sequences are extracted in the low frequency region of the host quantum audio frequency domain by quantum discrete cosine transform, and then the sequence is encrypted by Henon mapping to generate quantum zero watermark. By using the quantum circuit of Henon mapping as the quantum secret key of zero watermark, the security of quantum zero watermark algorithm is effectively improved. This paper designs the circuit diagram of quantum Henon map scrambling and quantum zero watermark generation and extraction algorithm, and verifies the feasibility of the zero watermark algorithm. Simulation results show that compared with the existing quantum audio watermarking algorithms, the quantum zero watermarking algorithm proposed in this paper has better imperceptibility and robustness.
-
0. 引言
量子计算和量子信息处理在并行计算、多任务处理及高效存储等方面展现出了巨大潜力，可以解决或改进传统领域中难以处理或计算的难题. 1982年，来自美国的物理学家Feynman首次提出了量子计算的概念[1]. 他指出直接利用经典计算机来模拟指数级增长的量子力学系统存在本质的困难，以此为基础创建的量子计算机对某些问题的处理能力将远远超过经典计算机. 这一理论的提出奠定了量子计算的基础. 1985年，Deutsch提出是否可以利用量子力学这一物理学的最终规律，根据经典图灵机的构造，创造出一种能够有效模拟任意物理系统的计算装置[2]. 特别地，他指出利用量子态的相干叠加性可以实现并行的量子计算，而且可以更加高效地解决在经典领域中存在的问题. 1994年，Shor提出大数因子分解问题和离散对数问题在量子计算领域范围内可以得到有效的解决[3]. 由于这两个问题在传统领域内没有有效的解决方法，使得以它们的计算安全为理论基础的经典保密通讯技术如RSA(Ron Rivest、Adi Shamir、Leonard Adleman)公钥密码体制[4]，受到了严峻的挑战. 同时，量子信息处理作为一种计算工具越来越多地应用于计算机科学领域，如量子机器学习[5]和量子图像处理[6]等. 量子计算基于量子力学的理论体系，完全超脱于经典计算模式及宏观概念.
量子计算机在计算速度和信息存储能力方面相比于经典计算机有着本质的超越，这种内在的计算优势使得很多学者相信经典计算机与量子计算机之间在计算能力上的差距是无法逾越的. 因此，在不久的将来，经典计算机在传统领域中的统治地位定会被一种更加成熟的计算模型所取代. 无论在存储效率及计算能力上传统计算机都将被全面超越. 此外，量子信息技术不仅仅局限于量子计算方面，在量子通讯(quantum information)[7]、量子密码学(quantum cryptography)[8]、量子隐形传态(quantum teleportation)[9-10]及量子密集编码(quantum dense coding)[11]等领域的发展也颇有成效. 最近，如何利用量子计算解决数字音频处理领域中的问题引起了中外学者的广泛关注[12-17].
2017年，Yan等[18]提出了一种可以双极表示数字音频振幅信息的量子表达式(flexible representation of quantum audio，FRQA)，这种表达式在直观上更加接近传统领域对数字音频的表示方法和真实的数字音频波形. 更重要地是，FRQA可以更加方便而有效地执行量子音频的基础操作. 另外，水印技术利用特殊的信息嵌入方法，把要传递的信息隐藏在宿主信息中. 基于FRQA表达式，Chen等提出了两种基于量子离散余弦变换(quantum discrete cosine transform，qDCT)的量子音频水印算法[19]. 利用qDCT很强的“能量集中”特性，即大多数的自然信号(如声音和图像)的能量都集中在离散余弦变换后的低频部分，提出了量子音频水印算法和分段量子音频水印算法，最后利用仿真实验对两种算法的不可感知性和鲁棒性进行了对比和分析.
本文针对算法的不可感知性和鲁棒性，提出了一种量子音频零水印算法. 利用量子离散余弦变换作用于宿主量子音频，基于加密后的频域内低频分量的序列特点生成该宿主量子音频的水印信息. 本文提出的算法与现有量子音频水印方法的最大区别是已有量子音频水印算法的水印信息可以是一幅量子图像或一段量子音频，再将量子水印信息嵌入到宿主量子音频中，而量子音频零水印的水印信息是通过宿主量子音频自身的结构特点提取出的一串不规则的二进制数列. 因此，本文提出的算法具有更好的不可感知性和更强的鲁棒性.
1. FRQA及量子操作单元
1.1 FRQA表达式
对于一个长度为2l的数字音频，其对应的FRQA表达式为
(1) 其中，|At>=|Atq-1…At1At0>对每一个振幅利用二进制补码的方式进行编码，|t>=|tl-1…t1t0>，ti∈{0，1}记录了与振幅对应的时间信息. 量子态|QA>是归一化的，满足‖|QA>‖=1. 从式(1)可以看出，FRQA需要q+l个量子位表示具有2l个采样点的量子音频信号.
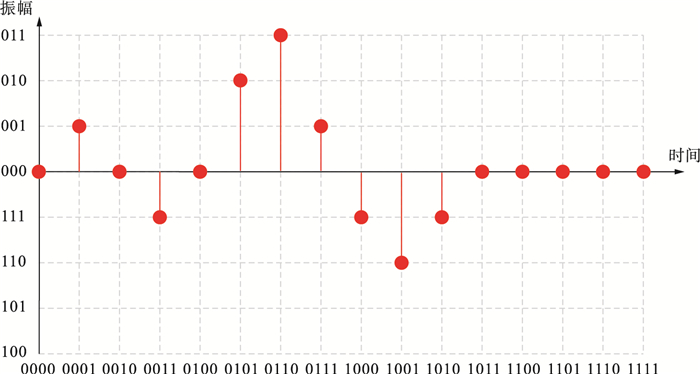
在图 1中展示了一段音频信号及如何用FRQA表达式对其进行表示. 在这个例子中，振幅的取值都是在-2到3之间，因此仅仅需要3个量子比特编码音频的振幅信息. 音频的长度是13，故l=∣lb13∣=4，因此，共需要7个量子位对这个FRQA量子音频进行表示.
![]()
图 1 音频示例及对应的FRQA表达式量子态算法1 量子零水印生成算法 1：宿主量子音频FRQA作为输入
利用H门初始化量子零水印序列的时间信息
2：qDCT作用于FRQA的时间域完成时域到频域的转换
3：根据宿主音频低频区域的振幅值为零水印序列赋值
4：利用密钥生成的Henon映射线路图对零水印加密
5：iqDCT令宿主量子音频完成频域到时域的转换1.2 量子逻辑门
在量子算法中，常常需要对输入的量子态进行一系列的变换操作以完成特定的逻辑功能. 量子逻辑门可以在一定的时间间隔内完成不同量子态之间的逻辑转换[20-21]，从而实现简单的逻辑运算. 表 1中的非门可以对一个量子位的态取反，用符号X表示. Hadamard门(H门)通常可以对一系列量子基本态执行初始化操作，对应计算过程如式(2)所示：
(2) 表 1 量子逻辑门Tab. 1. Quantum logic gates量子门 公式 转换 符号 非门 X=|0> < 1|+|1><0| X|0>=|1>
X|1>=|0>
H门 
控非门 CNOT=|0><0|⊗ I+|1><1|⊗X CNOT|00>=|00>
CNOT|01>=|01>
CNOT|10>=|11>
CNOT|11>=|10>
当量子寄存器中的n个量子位的量子态都为|0>时，H变换分别作用于n个量子位会生成2n个基本态的线性叠加，也可理解为经过H变换的作用后，量子态|00…0>转换为从0到2n-1所有二进制数的线性叠加，它们存在的概率均为1/2n.
受控非门作用于两个量子位，对于量子态|xy>，当|x>为|0>时，|y>保持原有的量子态不变；当|x>为|1>时，|y>执行取反操作，具体执行过程可以表述为
(3) 该变换实现了异或功能，故亦称CNOT门为量子异或门.
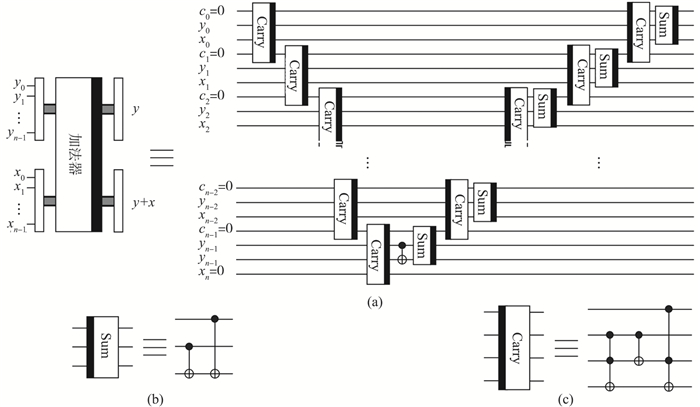
1.3 量子加法器
在文[20]中最先介绍了利用量子信息处理框架解决量子加法的计算问题，其目的是进行如下量子态之间的转换：
(4) 其中，|x>和|y>是两个量子态的输入，而输出为|x>和|x+y>. 如图 2所示，量子加法器由2n-1个进位模块(图中的“Carry”)和2n个求和模块(图中的“Sum”)组成. 此外，进位模块由2个Toffoli门和1个CNOT门组成，求和模块由2个CNOT门组成，如图 2中(b)和(c)所示.
2. 量子离散余弦变换
离散余弦变换(discrete cosine transform，DCT)在信号和图像处理领域的应用非常广泛，特别是对于有损压缩，例如MP3格式的数字音频压缩和JPEG格式的数字图像压缩[22]. 这些应用都利用了DCT很强的“能量集中”特性. 信号的DCT运算可以将其从时域变换到频域. DCT作用于音频或图像后，大部分信号信息往往集中在少量的低频分量中. 基于量子计算的DCT实现是一个非常复杂的过程，可以利用式(5)来实现量子DCT[23]，表示为qDCT：
(5) 其中，用m个量子位编码的|x>可以记录信号中一系列采样振幅的叠加态. 在执行qDCT的变换操作后，|x>被转化为|c>，而|c>用来记录在频域内采样点的振幅信息. 计算qDCT的方程为
(6) 其中，
(7) 同时，ω=exp(2πi/4N)，其中，i2=-1.
从式(7)中可以得出VN=π1(H⊗1N×N)，其中，π1是常量，1N×N是含有N行N列的单位矩阵. ⊗表示张量积，H指广泛应用于量子计算中的Hadamard矩阵. 此外，需要定义一个函数操作π1：在0≤x<2n的条件下，π1|0x>=|0x>且π1|1x>=|1x>.x表示对x中的量子比特取反的操作，其线路图包含1个量子控制比特和n个NOT门.
实现UN对于量子态的计算包括如下4种情况：
(8) 其中，x的取值范围为1≤x<2n，而y的取值范围为0≤y<2n-1，0和1分别表示含有n个量子位的|0…0>态和|1…1>态. 同时，对D1和TN进行定义：
(9) 另外，
(10) 其中，D1是一个对角矩阵，TN可以执行如下的操作：
(11) 其中，x的取值范围为1≤x<2n，i2=-1，此外，公式中x′=2n-x. 为了完成TN的运算，有如下的操作单元D(如果忽略TN中二进制补码的情况)：
(12) 为了实现式(12)中的操作，需要量子算符B=
从式(12)中可以计算出TN=π2D. 这里图 3(b)所表示的Pn可以完成一种映射操作：|x>→|x+1mod2n>. 为了计算式(9)中的D1，需要定义式(13)中Δ1、Δ2和C的3个操作算符：
(13) 其中，Lj=diag(1，ω2j-1)且Kj=diag(ω2j-1，1). 因此，D1=(C⊗1N)·(Δ1⊕Δ2). 此外，利用D0可以完成如下的操作D0|10>=i|10>或D0|x>=|x>. 基于此，定义一个π3的操作，π3|0x>=|0x>或π3|1x>=|1(x+1mod2n)>.
考虑一个关键公式：UN=D 1TND0π3，基于对D1和TN的计算，可以计算出如下公式：
(14) 通过定义D0和π3，可以获得如下计算结果D0π3|0x>=|0x>和D0π3|1x>=|1(x+1mod2n)>，进而通过计算得到D0π3|11>=i|10>. 此外，可以建立如下公式(x+1mod2n)′=. 通过结合D1TN、D0π3和式(10)中提出的TN=π2D，可以获得UN†的计算方法：
(15) 根据式(16)可以计算出D0Dt：
(16) 利用算符Bt和J可以实现提出的qDCT的计算过程，
3. 量子Henon映射加密
在量子零水印算法中需要添加一种量子加密算法对零水印信息进行加密，本节的Henon映射可以利用密钥生成一组随机序列. Henon映射的数学表达式为[24]
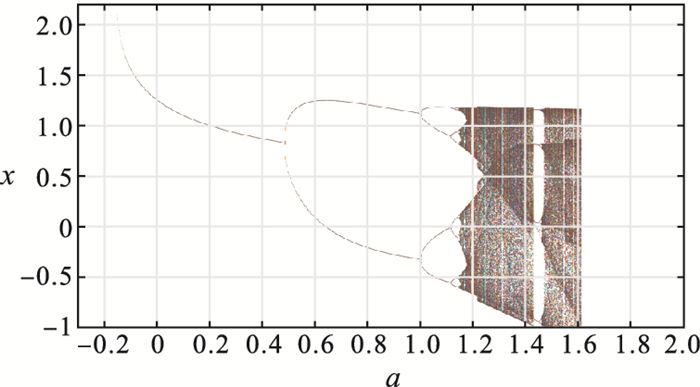
(17) Henon映射的参数a与b不同的选值会使序列x与y产生不同的效果：1) 若干次迭代后xn与yn的值会趋向于无穷大；2) 若干次迭代后xn与yn的值只取m个固定的数值，称此时的映射处于周期m的状态；3) xn与yn的取值是一组随机序列，此时称映射处于混沌状态. 因此，为了获取随机序列所选取的a与b的值，应该保证Henon映射处于混沌状态：
(18) 由式(17)可知，如果b的取值范围为|b|>1，经过多次计算迭代后，x与y序列的值趋向于无穷. 当b的值满足|b|≤1的同时，a应满足式(18)才可令序列的取值控制在有限的范围内. 最后利用图 4中的Henon映射分叉图来确定当为b赋值后a值的取值范围. 如图 4所示，当b=0.2时，a从-0.16开始进入周期1状态，随着a值的不断增加Henon映射出现了倍周期的分叉现象，当a>1.178后开始出现混沌现象且取值范围逐渐增大，直到1.613为止. 因此，当b=0.2时，a的取值应控制在1.178<a<1.613范围内. 同时应注意，当1.431≤a≤1.468时，Henon映射序列出现了周期窗口，在对参数a的值进行选取时也要同样避免这些窗口，这样的加密效果会相对更加理想.
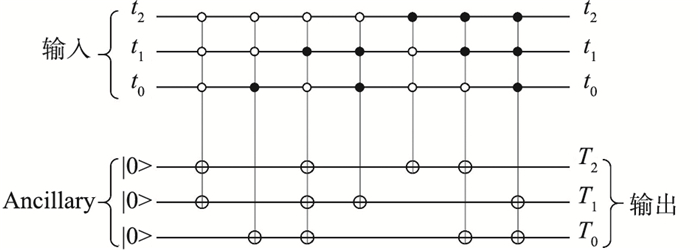
实验中选取常数a=1.51和b=0.2，同时x(0)=0.6和y(0)=0.7来获取所需的随机序列，利用式(17)计算出的随机序列为0.600 0，1.156 4，0.899 3，0.010 2，0.820 0，0.013 3，1.163 7，1.047 6. 把3位二进制数序列，即000，001，…，111与随机序列中的元素一一对应，再对此数列进行降序排列，同时二进制数列会重新排序，形成置乱后的二进制数列. 此过程如图 5所示.
![]()
图 5 随机序列降序排列置乱二进制数Fig. 5. Scramble binary numbers utilizing random sequence in descending order与图 5置乱过程对应的Henon映射量子线路图如图 6所示，其中t0、t1、t2是线路图的3个输入量子位，其存储了8个量子叠加态，即|000>，…，|111>. 与之对应的是3个Ancillary量子位，其是8个|000>量子态的叠加. t0、t1、t2上的控制位可以确定其所处的量子态，触发与之对应的3个Ancillary量子位上的量子非门(NOT门)，使初始态|000>变为Henon映射后的量子态. 如利用式(17)计算出的随机序列中的第1位小数为0.600 0，与之对应的二进制数为000. 如图 5所示，经过降序排列后的第1位二进制数为110. 因此在图 6中，如果令量子态|000>变为|110>，需要在两个高位量子位执行取反操作. 同理第2组变换是从量子态|000>变为|001>(NOT门作用于最低位)，第3组为|000>变为|111>(NOT门作用于3个量子位). 经过7轮控非门操作后，|T0T1T2>为线路图的3个量子输出位，为二进制置乱后顺序(如图 5最右侧一列)的叠加态. 由于二进制101置乱后对应的二进制数是000，这与3个Ancillary量子位初始化量子态|000>相同，此种情况下不需要控非门的变换，因此图 5中虽然有8个二进制数，但图 6的线路图中仅有7个控非门.
4. 基于Henon映射的量子音频零水印
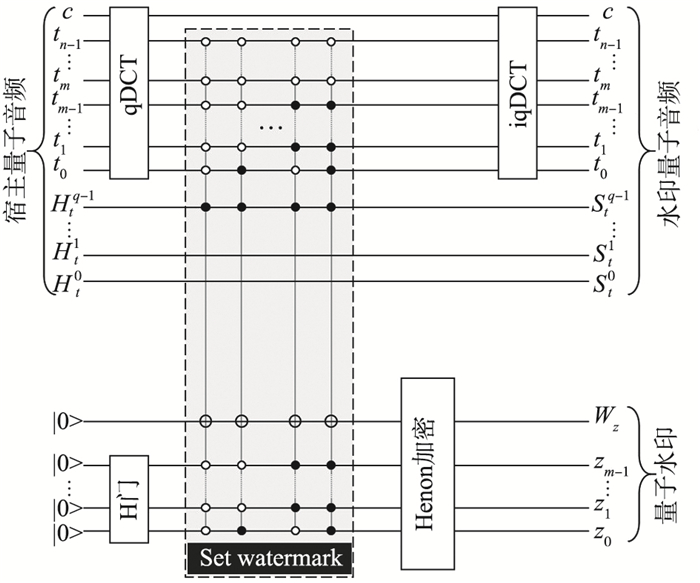
4.1 量子零水印概述
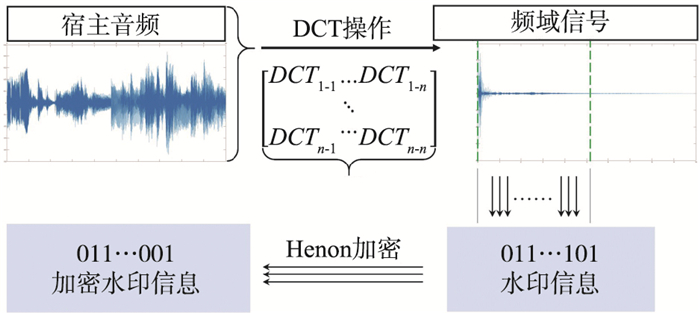
量子零水印算法示意图如图 7所示，首先利用量子离散余弦变换qDCT对FRQA格式编码的量子音频进行运算，其计算过程如下：
(19) qDCT将FRQA量子音频从时域转换为频域. |c>与|t>有一样的取值范围，即从|0>到|2l-1>，并记录FRQA音频在频域内的采样位置. 其次，提取宿主量子音频在频域内的低频分量，通过振幅二进制的最高位生成一个二进制序列，此为该宿主量子音频的量子水印信息. 这种提取算法保留了原宿主量子音频的所有信息，因此在算法的不可感知性方面有很大优势. 同时，水印信息的提取位置设定为低频分量，降低了传输过程中噪声对水印信息的影响，提高了算法的鲁棒性. 最后通过Henon映射加密算法对水印信息进行加密，从而获得最终的已加密的量子水印信息.
对于量子零水印的提取算法，首先仍然对含水印信息的量子音频进行qDCT处理，然后在频域内的低频区域用与提取算法相同的方法计算出一组二进制序列，最后利用特定的量子计算线路图对该组序列执行Henon映射，生成提取出的零水印二进制序列.
4.2 量子零水印生成算法
量子零水印生成算法如算法1所示，与之对应的线路图如图 8所示，其输入为FRQA格式编码的宿主量子音频以及初始化为|0>态的量子比特序列. 首先利用H门对处于|0>态的量子比特序列执行式(2)中的操作生成|0…0>，|0…1>，…，|1…1>的叠加态. 图中的qDCT表示量子离散余弦变换，作用于宿主量子音频存贮时间信息的量子比特序列，即|t0t1…tn-1>，使量子音频由时间域转换为频域. 虚线框中被命名为“Set watermark”区域完成了量子零水印的设置工作，这个过程中宿主量子音频中的量子控制位t0…tm-1与Hadamard门作用后的量子比特序列在每个控非门执行时保持一致. 表示量子振幅比特序列的最高量子位Htq-1控制下方二进制序列每个位置的具体值，当|Htq-1>=|1>时，控非门在对应量子位上执行取反操作，实现|0>→|1>的转变，否则该量子位保持|0>态不变. 在经过2m个控非操作后，“Set watermark”部分完成. 之后对该二进制序列执行量子Henon映射加密算法(见第3小节)，生成已置乱的二进制序列，即量子零水印，图中用|z0…zm-1Wz>表示，其中Wz表示零水印序列每一位二进制的值，|z0…zm-1>表示零水印序列的下标序号. 最后的iqDCT表示量子反向离散余弦变换，使得宿主量子音频由频域转换回时间域，从而完成量子零水印的生成算法.
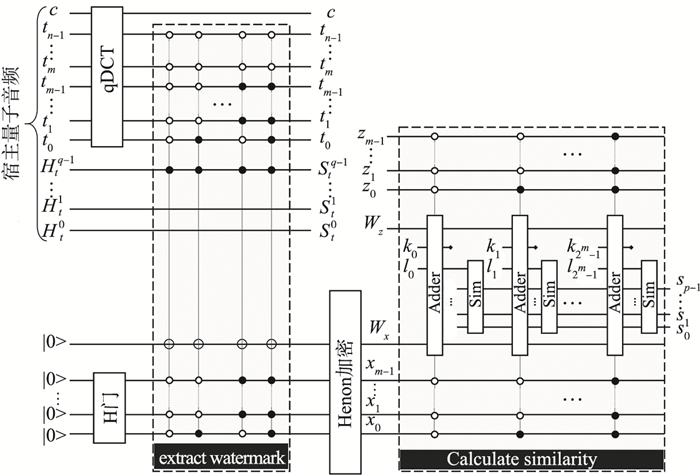
4.3 量子零水印提取算法
量子零水印提取算法如算法2所示，与之对应的量子零水印提取算法线路图如图 9所示，其线路图的两个输入与零水印生成算法相同，分别为宿主量子音频与初始化为|0>态的量子比特序列. 首先，与图 8相同，利用H矩阵与qDCT变换初始化量子比特序列和完成宿主量子音频从时域向频域的转变. 其次，利用与零水印生成算法相同的线路图对量子比特序列进行设置，生成值为|0>或|1>的二进制量子比特序列. 之后，利用量子Henon映射加密算法对该二进制量子比特序列进行处理，其线路图必须与量子零水印生成算法中Henon映射的线路图完全一致，从而获得提取出的量子零水印.
图 9中“Calculate similarity”把生成的量子零水印序列与标准的水印量子比特序列进行逐位比较，同时计算两个序列的相似度. |z0…zm-1Wt>表示标准量子零水印，|x0…xm-1Wx>表示从量子音频中提取的零水印信息. “Adder”表示量子加法器(见1.3节)，其两个输入是两个量子位|Wt>和|Wx>，|z0…zm-1>与|x0…xm-1>是加法器的2m个量子控制位，控制加法器的执行条件，即在两个量子零水印序列的相同位置执行量子加法的操作，|k0l1>两个量子位记录加法器的结果. 此处有一个规律，即两个二进制数相加，如果它们的值相等(即相加的两个二进制数都为0或都为1)，则它们和的低位一定为0，如00+00=00或01+01=10，因此可以看出，相同的两个二进制数相加，其结果的低位一定为0. 相反地，如果相加的两个二进制数的值不同(即相加的两个二进制数一个为0，而另一个为1)，则它们和的低位一定为1，如00+01=01或01+00=01，故当两个相加的二进制数不同时，它们和的低位一定为1. 因此，只需把量子加法器相加结果的低位执行叠加操作，其结果就是两个零水印序列的相似性测度，其结果越小说明相似度越高.
图 9中的“Sim”模块计算相似性测度，其输入为多个初始化为|0>态的量子比特. 另一个输入为“Adder”的低位输出量子位|l0>，在“Sim”中同样执行量子加法的操作，其结果为下一个“Sim”模块的输入，同时另一个输入为第二个“Adder”的低位输出量子位|l1>，由此经过2m个叠加操作后可以计算出相似性测度，图中为整个线路图的输出|s0s1…sp-1>.
5. 仿真实验
利用Matlab进行仿真实验模拟量子音频零水印算法的执行过程. 宿主量子音频利用FRQA的量子音频表达式进行编码，分配9个量子位表示振幅信息，19个量子位表示时间信息. 利用19个量子位存储二进制序列零水印，零水印的大小为218，利用18个量子位表示零水印序列的下标，用一个量子位表示零水印序列的大小.
量子水印算法的目的是通过隐藏水印信息实现对量子音频的版权保护. 不可感知性可以度量在宿主音频内是否容易察觉到水印的存在. 水印算法的这种性质是判定消息安全性的重要指标. 鲁棒性可以测试含水印的音频在遭受恶意攻击或受到信道中噪声的作用时，保证水印信息不受影响的能力. 不可感知性和鲁棒性是评价水印算法性能优劣的两个重要参数.
5.1 不可感知性
不可感知性是为了测试量子零水印算法执行了嵌入操作后，含水印的音频与嵌入前的宿主音频之间的不同. 通常计算两种音频信号间的信噪比(signal-to-noise ratio，SNR)来对零水印算法的不可感知性进行量化. 信噪比计算信号功率与噪声功率的比值，单位为分贝(dB)，其公式为
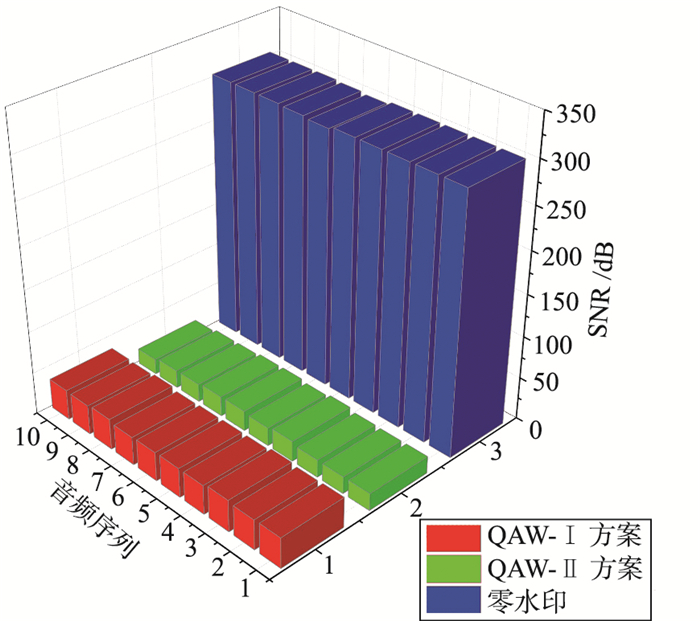
(20) 其中，Ht为宿主量子音频，St为嵌入水印后的含水印信息的量子音频，n为编码两种量子音频时间信息的量子位个数. 信噪比的值越高证明算法不可感知性越强. 实验中选取10种不同的宿主音频(如图 10)进行测试，分别对其进行零水印处理及文[19]中两种量子音频水印算法的嵌入操作，进而生成对应的已嵌入水印信息的量子音频. 最后将嵌入前的宿主量子音频与嵌入后的含水印量子音频代入式(20)计算SNR值.
3种不同的量子音频水印算法针对10种宿主音频执行水印嵌入操作后所计算出的SNR值如图 11所示. 蓝色、红色和绿色分别对应零水印、QAW-Ⅰ(quantum audio watermarking-Ⅰ)和QAW-Ⅱ(quantum audio watermarking-Ⅱ)水印嵌入算法，从图中数据分析可知10种宿主音频的零水印嵌入算法获得的SNR值要远远高于QAW-Ⅰ和QAW-Ⅱ水印嵌入算法，说明零水印的不可感知性要高于其他两种量子音频水印算法. 这是因为与普通水印嵌入算法不同，零水印算法是从宿主量子音频本身提取出水印信息，在产生水印的过程中宿主音频的状态完全不受影响，这也是零水印算法最大的优势，即具有强健的不可感知性.
![]()
图 11 3种量子音频水印算法的SNR值Fig. 11. The SNR values among three quantum audio watermarking algorithms5.2 鲁棒性
利用鲁棒性对量子音频零水印算法的稳健性(抗干扰和抗攻击能力)进行探讨. 通常使用归一化互相关系数(normalized correlation coefficient，NCC)来对零水印算法的鲁棒性进行量化. NCC可以确定两个序列之间的相似性，数值越大，表示算法的鲁棒性越强. NCC的计算公式为
(21) 其中，W和Wex表示原始水印序列和从含水印的量子音频中提取的水印序列. wex(i)表示坐标位置为i的水印信息. NCC值越高(NCC∈[0, 1])，表明原始量子水印与提取出的量子水印越相似.
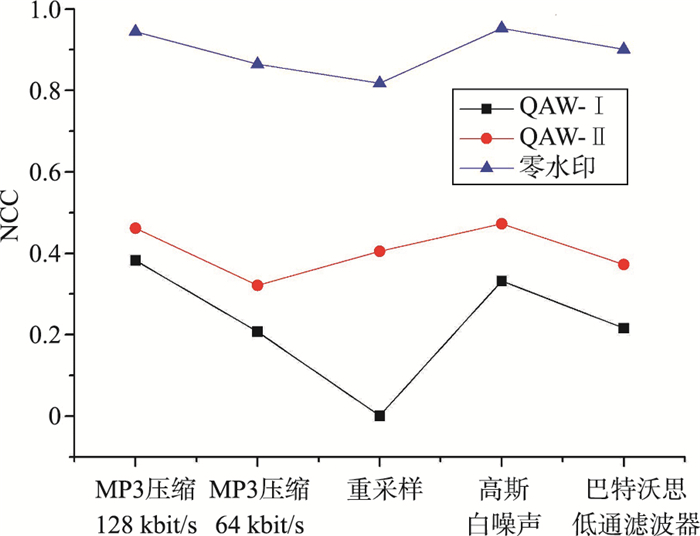
与文[19]中提出的两种量子水印算法的鲁棒性进行对比，设置相同的实验条件. 在执行了零水印生成算法后，对量子音频进行不同类型的攻击，从零水印提取方法中获得的水印序列与标准零水印序列进行比较，可以用式(21)中的NCC值对鲁棒性进行量化分析，NCC值越高，说明算法具有更强的鲁棒性. 在实验中利用MP3压缩、高斯白噪声(WGN)、巴特沃思(Butterworth)低通滤波器和重采样四种攻击方法，对本文提出量子零水印算法的鲁棒性进行测试并与文[19]中的两种算法进行比较. MP3压缩又分为两种压缩情况：128 kbit/s和64 kbit/s. 表 2中总结了3种量子音频水印算法的NCC值. 显然，本文提出的量子零水印算法在5种不同仿真攻击下NCC值最大，说明其算法的鲁棒性最强，同时表明量子零水印算法对旨在破坏量子音频水印的攻击方面具有更好的鲁棒性.
表 2 3种水印算法NCC值比较Tab. 2. The NCC comparison among three watermarking algorithms攻击类型 NCC值
(QAW-Ⅰ)NCC值
(QAW-Ⅱ)NCC值
(零水印)MP3压缩(128 kbit/s) 0.382 5 0.461 7 0.944 2 MP3压缩(64 kbit/s) 0.207 3 0.321 5 0.864 5 重采样 0.001 2 0.405 2 0.817 8 高斯白噪声 0.332 1 0.472 8 0.952 6 巴特沃思低通滤波器 0.216 6 0.372 7 0.900 9 图 12更加明确地展示了3种水印算法在不同攻击下NCC值的不同，很明显图中蓝色所代表的零水印算法在5种不同攻击下的NCC值比其它两种量子音频水印算法都要高出很多. 因此，量子音频零水印算法具有较高的鲁棒性.
根据本小节的仿真实验可以证明量子音频零水印算法在不可感知性和鲁棒性方面相比于同样基于量子离散余弦变换的将水印信息直接嵌入的量子音频水印算法具有更大的优势.
6. 总结
本文提出了一种基于量子离散余弦变换的量子零水印算法，宿主量子音频被编码为FRQA格式，利用qDCT获得宿主量子音频的频域，再根据其低频区域的大小形成一组量子比特序列. 为了对生成的量子比特序列加密，本文根据Henon映射加密算法提出一种量子映射加密算法，对量子比特序列进行加密操作，从而获得量子零水印，用于保护量子音频的版权信息. 此处，量子Henon映射的线路图即为提取量子零水印的秘钥. 可以用相似的方法完成量子零水印的提取工作，但前提是需要掌握Henon映射完整的量子线路图才有可能提取出正确的量子零水印信息. 最后利用仿真实验，验证了本文提出算法具有强健的不可感知性和更强的鲁棒性.
-
![]()
图 1 音频示例及对应的FRQA表达式量子态
Figure 1. A segment of audio and its corresponding FRQA representation quantum state
![]()
图 5 随机序列降序排列置乱二进制数
Figure 5. Scramble binary numbers utilizing random sequence in descending order
![]()
图 11 3种量子音频水印算法的SNR值
Figure 11. The SNR values among three quantum audio watermarking algorithms
算法1 量子零水印生成算法 1：宿主量子音频FRQA作为输入
利用H门初始化量子零水印序列的时间信息
2：qDCT作用于FRQA的时间域完成时域到频域的转换
3：根据宿主音频低频区域的振幅值为零水印序列赋值
4：利用密钥生成的Henon映射线路图对零水印加密
5：iqDCT令宿主量子音频完成频域到时域的转换
下载: 导出CSV
表 1 量子逻辑门
Table 1 Quantum logic gates
量子门 公式 转换 符号 非门 X=|0> < 1|+|1><0| X|0>=|1>
X|1>=|0>H门 控非门 CNOT=|0><0|⊗ I+|1><1|⊗X CNOT|00>=|00>
CNOT|01>=|01>
CNOT|10>=|11>
CNOT|11>=|10>
下载: 导出CSV
表 2 3种水印算法NCC值比较
Table 2 The NCC comparison among three watermarking algorithms
攻击类型 NCC值
(QAW-Ⅰ)NCC值
(QAW-Ⅱ)NCC值
(零水印)MP3压缩(128 kbit/s) 0.382 5 0.461 7 0.944 2 MP3压缩(64 kbit/s) 0.207 3 0.321 5 0.864 5 重采样 0.001 2 0.405 2 0.817 8 高斯白噪声 0.332 1 0.472 8 0.952 6 巴特沃思低通滤波器 0.216 6 0.372 7 0.900 9
下载: 导出CSV
-
[1] Feynman R. Simulating physics with computers[J]. International Journal of Theoretical Physics, 1982, 21(6/7): 467-488.
[2] Deutsch D. Quantum theory, the church-turing principle and the universal quantum computer[C]//Royal Society of London A. London, UK: Royal Society, 1985: 97-117.
[3] Shor P. Algorithms for quantum computation: Discrete logarithms and factoring[C]//35th Annual Symposium on Foundations of Computer Science. Piscataway, USA: IEEE, 1994: 124-134.
[4] Rivest R, Shamir A, Adleman L. A method for obtaining digital signatures and public-key cryptosystems[J]. Communications of the ACM, 1987, 21(2): 120-126.
[5] Biamonte J, Wittek P. Quantum machine learning[J]. Nature, 2017, 549: 195-202. doi: 10.1038/nature23474
[6] Yan F, Venegas-Andraca S. Quantum image processing[M]. Berlin, Germany: Springer, 2020.
[7] Ge W, Sawyer B C, Britton J W, et al. Trapped ION quantum information processing with squeezed phonons[J]. Physical Review Letters, 2019, 122(3): 030501. doi: 10.1103/PhysRevLett.122.030501
[8] Molotkov S. Concatenation of keys in quantum cryptography: How quantum entanglement "penetrates to" classical devices[J]. Journal of Experimental and Theoretical Physics, 2018, 127(4): 627-637. doi: 10.1134/S1063776118090066
[9] Bouwmeester D, Pan J, Mattle K, et al. Experimental quantum teleportation[J]. Nature, 1997, 390: 575-579. doi: 10.1038/37539
[10] Yoshida B, Yao N Y. Disentangling scrambling and decoherence via quantum teleportation[J]. Physical Review X, 2019, 9(1): 011006. doi: 10.1103/PhysRevX.9.011006
[11] Roy S, Chanda T, Das T, et al. Deterministic quantum dense coding networks[J]. Physics Letters A, 2018, 382(26): 1709-1715. doi: 10.1016/j.physleta.2018.04.033
[12] Zhang W W, Gao F, Liu B, et al. A quantum watermark protocol[J]. International Journal of Theoretical Physics, 2013, 52(2): 504-513. doi: 10.1007/s10773-012-1354-9
[13] Yang Y G, Jia X, Xu P, et al. Analysis and improvement of the watermark strategy for quantum images based on quantum Fourier transform[J]. Quantum Information Processing, 2013, 12(8): 2765-2769. doi: 10.1007/s11128-013-0561-5
[14] Song X H, Wang S, Liu S, et al. A dynamic watermarking scheme for quantum images using quantum wavelet transform[J]. Quantum Information Processing, 2013, 12(2): 3689-3706.
[15] Yang Y G, Xu P, Tian J, et al. Analysis and improvement of the dynamic watermarking scheme for quantum images using quantum wavelet transform[J]. Quantum Information Processing, 2014, 13(9): 1931-1936. doi: 10.1007/s11128-014-0783-1
[16] Song X H, Wang S, Abd El-Latif A, et al. Dynamic watermarking scheme for quantum images based on Hadamard transform[J]. Multimedia Systems, 2014, 20(4): 379-388. doi: 10.1007/s00530-014-0355-3
[17] Wang J. QRDA: Quantum representation of digital audio[J]. International Journal of Theoretical Physics, 2016, 55: 1622-1641. doi: 10.1007/s10773-015-2800-2
[18] Yan F, Iliyasu A, Guo Y M, et al. Flexible representation and manipulation of audio signals on quantum computers[J]. Theoretical Computer Science, 2017, 752(15): 71-85.
[19] Chen K H, Yan F, Iliyasu A, et al. Dual quantum audio watermarking schemes based on quantum discrete cosine transform[J]. International Journal of Theoretical Physics, 2019, 58(2): 502-521. doi: 10.1007/s10773-018-3950-9
[20] Vlatko V, Adriano B, Artur E. Quantum networks for elementary arithmetic operations[J]. Physical Review A, 1996, 54(1): 147-153. doi: 10.1103/PhysRevA.54.147
[21] Deutsch D. Quantum computational networks[J]. Royal Society of London A: Mathematical, Physical and Engineering Sciences, 1989, 425(1868): 73-90. doi: 10.1098/rspa.1989.0099
[22] Ahmed N, Natarajan T, Rao K. Discrete cosine transform[J]. IEEE Transactions on Computers, 1974, C-23(1): 90-93. doi: 10.1109/T-C.1974.223784
[23] Klappenecker A, Rotteler M. Discrete cosine transforms on quantum computers[C]//2nd International Symposium on Image and Signal Processing and Analysis. Piscataway, USA: IEEE, 2001: 464-468.
[24] Hénon M. A two-dimensional mapping with a strange attractor[J]. Communications in Mathematical Physics, 1976, 50: 69-77. doi: 10.1007/BF01608556
-
期刊类型引用(1)
1. 宋杨，秦坤. 网络多段支持度数字音频信息动态加密算法. 计算机仿真. 2024(12): 450-454 . 
百度学术
其他类型引用(2)
计量
- 文章访问数: 217
- HTML全文浏览量: 9
- PDF下载量: 185
- 被引次数: 3
